Vijos-P1103题解【线段树】

本文为原创，转载请注明：http://www.cnblogs.com/kylewilson/

题目出处：

https://www.vijos.org/p/1103

题目描述：

一条马路从数轴0到L，每个位置0，1，2，......，L都有一棵树，现需要将一些区间的树清除，区间可能有交集，求清除后还剩下多少棵树？

输入：

输入的第一行有两个整数：L（1 <= L <= 10000）和 M（1 <= M <= 100），L代表马路的长度，M代表区域的数目，L和M之间用一个空格隔开。接下来的M行每行包含两个不同的整数，用一个空格隔开，表示一个区域的起始点和终止点的坐标。

500 3

150 300

100 200

470 471

思路分析：

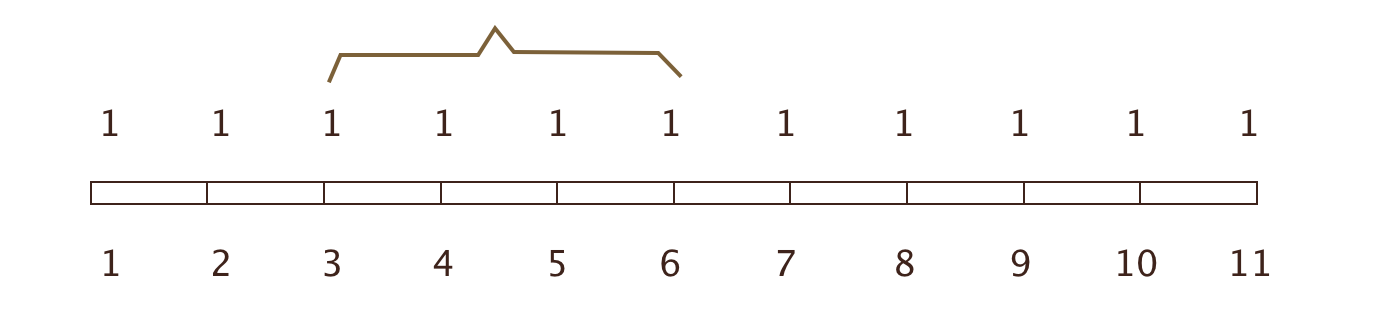
第一感觉，可以用数组a[10000]来模拟马路上的树，1表示有树，每次操作，则将对应区间所有点改为0，最终统计为1的点，但时间复杂度O(L*M)，这明显不是最优的解法；

再仔细一想，每次都是对一个区间进行操作，而且对每一个点的操作都是相同的，所以考虑是否可以批量操作。

对于批量操作区间有线段树，树状树组等算法，本文讨论用线段树来解，树状树组算法以后会详细介绍。

那么问题来了，为什么会想到用线段树来解呢？即线段树能解决哪类问题？

线段树关键点：大区间的操作及结果等价于两个相邻的子区间操作及结果。

每次对马路上的树进行区间操作，如移除区间[a,b]上的树，也等价于移除区间[a,k]，[k+1,b](a<=k<=b)上的树；

并且当区间上的树已经移除后，再重复移除也对最终结果无影响

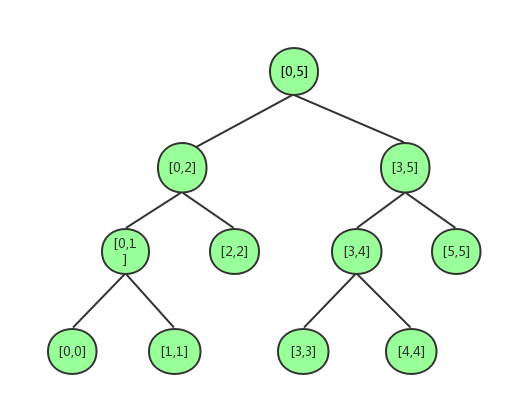
如上图，树中每个节点表示一段区间

每个节点需要记录如下关键信息

left: 区间左起点

right: 区间右终点

count: 区间还剩下的树，初始为right-left+1;

1）更新树时，如果区间在需要操作的范围内，则将区间所有树清除，即count=0，直接返回，不需要再去清除所有子节点；

2）父节点同时更新count值，father.count=lson.count+right.count;

　　当父节点已经为0，则说明该区间已经全部被清除，此时左右子节点之和可能不等于0，看1)中并没有去清除子节点；

　　所以父节点还是保持0

最终剩下的树即为根节点中的树，即root.count。

C++源码如下：

github: https://github.com/Kyle-Wilson1/Vijos/tree/master/P1103

#include <iostream>
#include <fstream>

using namespace std;

struct SegmentTree {
    int left, right, count;
    SegmentTree *lson, *rson;
};

SegmentTree *buildTree(int l, int r) {
    if (l > r) {
        return nullptr;
    }
    if (l == r) {
        auto *root = new SegmentTree{l, r, 1, nullptr, nullptr};
        return root;
    }
    auto *root = new SegmentTree{l, r, r - l + 1, nullptr, nullptr};
    int mid = (l + r) >> 1;
    root->lson = buildTree(l, mid);
    root->rson = buildTree(mid + 1, r);
    return root;
}

void removeRegion(SegmentTree *root, int regionLeft, int regionRight) {
    if (root->left >= regionLeft && root->right <= regionRight) {
        root->count = 0;
        return;
    }
    if (root->right < regionLeft || root->left > regionRight) {
        return;
    }
    removeRegion(root->lson, regionLeft, regionRight);
    removeRegion(root->rson, regionLeft, regionRight);
    root->count = min(root->count, root->lson->count + root->rson->count);
}

int main() {

    ifstream fin("a.in");
    ofstream fout("a.out");

    int l, m, i = 0, regionLeft, regionRight;
    fin >> l >> m;
    SegmentTree *root;
    //build segment tree
    root = buildTree(0, l);

    for (i = 0; i < m; i++) {
        fin >> regionLeft >> regionRight;
        removeRegion(root, regionLeft, regionRight);
    }

    fout << root->count;
    deleteMem(root);
    fin.close();
    fout.close();
    return 0;
}