五角星形线的笛卡尔坐标方程式可设为：

r=10+(3*sin(θ*2.5))^2 

x=r*cos(θ)

y=r*sin(θ)              （0≤θ≤2π）

根据这个曲线方程，在[0,2π]区间取一系列角度值，根据给定角度值计算对应的各点坐标，然后在计算出的坐标位置绘制一个填充色交替变换的小圆，从而得到沿五角星形线摆动的小圆的动画效果。

编写如下的HTML代码。

<!DOCTYPE html>

<html>

<head>

<title>沿曲线摆动的小圆</title>

</head>

<body>

<canvas id="myCanvas" width="400" height="400" style="border:3px double #996633;">

</canvas>

<script type="text/javascript">

var canvas = document.getElementById('myCanvas');

var context = canvas.getContext('2d');

var i = 0;

var j = Math.PI/32;

var t = 0;

var col = ['red','orange','yellow','green','cyan','blue','magenta'];

function loop()

{

t = t + 1;

i = i + j;

if (t > 6) { t = 0; }

var r=10+9*Math.sin(2.5*i)*Math.sin(2.5*i);

var x = 7*r*Math.cos(i)+200;

var y = 7*r*Math.sin(i)+200;

context.beginPath();

context.moveTo(200, 200);

context.lineTo(x, y);

context.lineCap = 'round';

context.strokeStyle = 'rgba(50,100,255,0.6)';

context.stroke();

context.beginPath();

context.moveTo(200, 200);

context.arc(x, y, 8, 0, 2 * Math.PI);

context.fillStyle = col[t];

context.fill();

if (i>2*Math.PI)

{

j =-Math.PI/32;

context.clearRect(0, 0, 400, 400);

}

if (i<0)

{

j = Math.PI/32;

context.clearRect(0, 0,400, 400);

}

}

setInterval('loop()',300);

</script>

</body>

</html>

在浏览器中打开包含这段HTML代码的html文件，可以在浏览器窗口中呈现出如图1所示的沿五角星形线摆动的小圆动画效果。

图1  沿五角星形线摆动的小圆

将上面程序中的语句

var r=10+9*Math.sin(2.5*i)*Math.sin(2.5*i);

var x = 7*r*Math.cos(i)+200;

var y = 7*r*Math.sin(i)+200;

改写为：

var e=80*(1+Math.cos(2*i)/4);

var f=e*(1+Math.sin(4*i));

var x=200+f*Math.cos(i);

var y=200-f*Math.sin(i);

就可以在画布中看到如图2所示的沿四瓣花型线摆动的小圆。

图2  沿四瓣花型线摆动的小圆

若改写为：

var r = 200 * Math.pow(Math.cos(i/3),3);

var x = 200 + r * Math.sin(i);

var y = 110 + r * Math.cos(i);

同时修改  if (i>2*Math.PI)  为         if (i>3*Math.PI)

就可以在画布中看到如图3所示的沿苹果形线摆动的小圆。

图3  沿苹果形线摆动的小圆

若改写为：

var r=100*Math.pow(Math.cos(2*i),0.5);

var x = 200 + 160*Math.sin(i)*Math.sin(i)*Math.sin(i);

var y = -(-170+ 10*(13*Math.cos(i)- 5*Math.cos(2*i) - 2*Math.cos(3*i) - Math.cos(4*i)));

就可以在画布中看到如图4所示的沿心形线摆动的小圆。

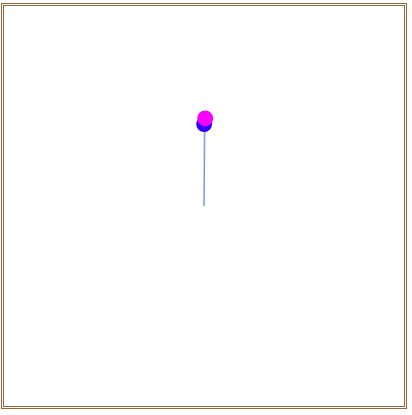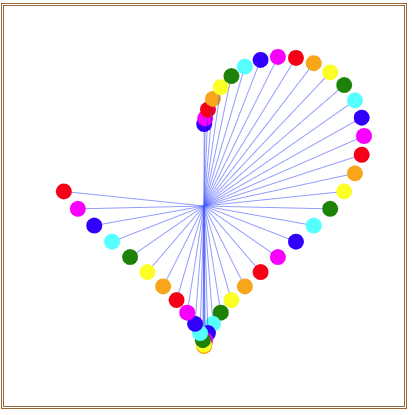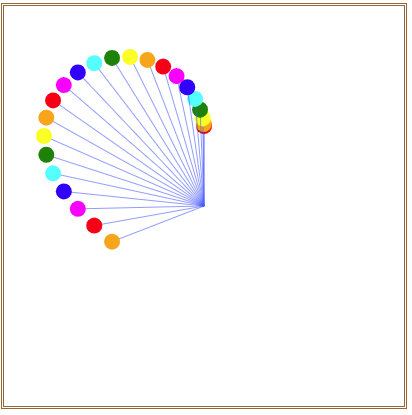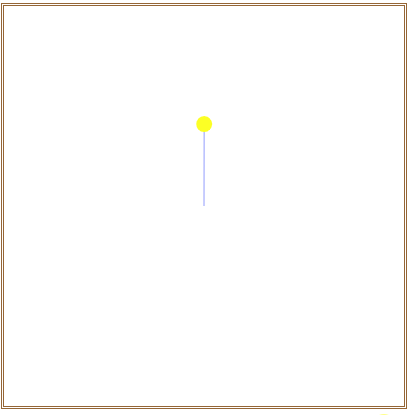
图4  沿心形线摆动的小圆

有兴趣的读者，可以根据自己感兴趣的曲线的参数方程，适当修改坐标位置（x,y）的计算语句，就可以看到沿指定曲线摆动的小圆的动画效果。

JavaScript动画实例：沿五角星形线摆动的小圆的更多相关文章

  1. JavaScript动画实例：递归分形图动态展示

    在“JavaScript图形实例:SierPinski三角形” 和“JavaScript图形实例:Levy曲线及其变形”等文章中我们介绍了通过递归生成分形图形的方法.我们可以将绘制的分形图形每隔一定的 ...

  2. JavaScript动画实例：李萨如曲线

    在“JavaScript图形实例:阿基米德螺线”和“JavaScript图形实例:曲线方程”中,我们学习了利用曲线的方程绘制曲线的方法.如果想看看曲线是怎样绘制出来的,怎么办呢?编写简单的动画,就可以 ...

  3. JavaScript动画实例：曲线的绘制

    在“JavaScript图形实例:曲线方程”一文中,我们给出了15个曲线方程绘制图形的实例.这些曲线都是根据其曲线方程,在[0,2π]区间取一系列角度值,根据给定角度值计算对应的各点坐标,然后在计算出 ...

  4. JavaScript图形实例：五角星

    1．五角星 在半径为80的圆周上取5个点,用这5个点依次首尾连接画5条线,可以绘制出一个五角星图案. 编写如下的HTML代码. <!DOCTYPE html> <head> & ...

  5. JavaScript动画实例：旋转的圆球

    1．绕椭圆轨道旋转的圆球 在Canvas画布中绘制一个椭圆,然后在椭圆上绘制一个用绿色填充的实心圆.之后每隔0.1秒刷新,重新绘制椭圆和实心圆,重新绘制时,实心圆的圆心坐标发生变化,但圆心坐标仍然位于 ...

  6. JavaScript动画实例：动感小球

    已知圆的坐标方程为: X=R*SIN(θ) Y=R*COS(θ)     (0≤θ≤2π) 将0~2π区间等分48段,即设定间隔dig的值为π/24.θ初始值从0开始,按曲线方程求得坐标值(x,y), ...

  7. JavaScript动画实例：旋转的正三角形

    给定一个正三角形的重心坐标为(x0,y0),高为h,可以用如下的语句绘制一个底边水平的正三角形. ctx.beginPath(); ctx.moveTo(x0,y0-h*2/3); ctx.lineT ...

  8. JavaScript动画实例：炸开的小球

    1．炸开的小球 定义一个小球对象类Ball,它有6个属性:圆心坐标(x,y).小球半径radius.填充颜色color.圆心坐标水平方向的变化量speedX.圆心坐标垂直方向的变化量speedY. B ...

  9. JavaScript动画实例：螺旋线

    数学中有各式各样富含诗意的曲线,螺旋线就是其中比较特别的一类.螺旋线这个名词来源于希腊文,它的原意是“旋卷”或“缠卷”.例如,平面螺旋便是以一个固定点开始向外逐圈旋绕而形成的曲线.在2000多年以前, ...

随机推荐

  1. 菜渣开源一个基于 EMIT 的 AOP 库(.NET Core)

    目录 1,快速入门 1.1 继承 ActionAttribute 特性 1.2 标记代理类型 2,如何创建代理类型 2.1 通过API直接创建 2,创建代理类型 通过API 通过 Microsoft. ...

  2. 循序渐进VUE+Element 前端应用开发(12）--- 整合ABP框架的前端登录处理

    VUE+Element 前端是一个纯粹的前端处理,前面介绍了很多都是Vue+Element开发的基础,从本章随笔开始,就需要进入深水区了,需要结合ABP框架使用(如果不知道,请自行补习一下我的随笔:A ...

  3. C/S C# WPF锐浪报表教程

    前言:锐浪报表是一种中国式报表的报表开发工具.博主使用锐浪报表有一段时间了,积累了一些经验希望能帮助你快速掌握并使用 第一章:集成项目 首先我们先去锐浪报表官网下载并安装锐浪报表. 创建WPF应用程序 ...

  4. C++ 公有继承、保护继承和私有继承的对比

    在c++的继承控制中,有三种不同的控制权限,分别是public.protected和private.定义派生类时,若不显示加上这三个关键字,就会使用默认的方式,用struct定义的类是默认public ...

  5. Java对MongoDB的CRUD

    https://blog.51cto.com/aiilive/1339058 MongoDB提供的Java操作API可以说是对Mongo数据库命令的Java翻译,熟悉Mongo命令,熟悉Java操作数 ...

  6. 10、一个action中处理多个方法的调用第二种方法method的方式

    在实际的项目中,经常采用现在的第二种方式在struct.xml中采用清单文件的方式 我们首先来看action package com.bjpowernode.struts2; import com.o ...

  7. 【Vim命令】

    命令 操作 :set nu 显示行号  i 编辑模式  :wq  修改并退出  :%s/a/b  把所有的a替换成b                        

  8. keras训练实例-python实现

    用keras训练模型并实时显示loss/acc曲线,(重要的事情说三遍:实时!实时!实时!)实时导出loss/acc数值(导出的方法就是实时把loss/acc等写到一个文本文件中,其他模块如前端调用时 ...

  9. Python之浅谈基础

    执行python的两种方式 交互式(jupyter) 通过cmd或jupyter运行python代码 优点:运行一句执行一句 缺点:关闭cmd或jupyter后数据消失 命令行式(pycharm) 优 ...

  10. P2629 【好消息，坏消息】

    其实刚开始看到这道题,应该很多都会想到区间DP中的合并石子,开一个2倍的空间(严格来说的话应该是2n-1),将本来的环变成一个链式的结构.然后对于得到的消息,可以预处理一个前缀和,这样就可以很方便的知 ...