(转载)微软数据挖掘算法：Microsoft Naive Bayes 算法（3）

介绍:

Microsoft Naive Bayes 算法是一种基于贝叶斯定理的分类算法，可用于探索性和预测性建模。 Naïve Bayes 名称中的 Naïve 一词派生自这样一个事实：该算法使用贝叶斯技术，但未将可能存在的依赖关系考虑在内。

和其他 Microsoft 算法相比，此算法所需运算量较少，因而有助于快速生成挖掘模型，从而发现输入列与可预测列之间的关系。 可以使用该算法进行初始数据探测，然后根据该算法的结果使用其他运算量较大、更加精确的算法创建其他挖掘模型。

算法的原理

在给定可预测列的各种可能状态的情况下， Microsoft Naive Bayes 算法将计算每个输入列的每种状态的概率。

若要了解其工作原理，请使用 Microsoft 中的 SQL Server Data Tools (SSDT) Naive Bayes 查看器（如下图所示）来直观地查看该算法分布状态的方式。

此处， Microsoft Naive Bayes 查看器可列出数据集中的每个输入列。如果提供了可预测列的每种状态，它还会显示每一列中状态的分布情况。

您将利用该模型视图来确定对区分可预测列状态具有重要作用的输入列。

例如，在此处显示的“Commute Distance”行中，输入值的分布对于购买者和非买者存在明显的不同。 这表明，“Commute Distance = 0-1 miles”输入可能是一个预测因子。

该查看器还提供了分布的值，这样您便能看到，对于上下班路程为一至二英里的客户，其购买自行车的概率是 0.387，不购买自行车的概率是 0.287。 在本示例中，该算法使用从诸如上下班路程之类的客户特征得出的数字信息来预测客户是否会购买自行车。

有关使用 Microsoft Naive Bayes 查看器的详细信息，请参阅使用 Microsoft Naive Bayes 查看器浏览模型。

应用场景介绍

通过前面两种算法的应用场景介绍，此次总结的Microsoft Naive Bayes 算法也同样适用，但本篇的Microsoft Naive Bayes算法较上两种算法跟简单，或者说更轻量级。

该算法使用贝叶斯定力，但是没有将属性间的依赖关系融入进去，也就是跟简单的进行预测分析，因此该假定成为理想化模型的假定，简单点说：贝叶斯算法就是通过历史的属性值进行简单的两种对立状态的推算，而不会考虑历史属性值之间的关系，这也就造成了它预测结果的局限性，不能对离散或者连续值进行预测，只能对两元值进行预测，比如：买/不买、是/否、会/不会等，汗..挺符合中国的易经学中太极图..凡事只有两种状态可以解释，正所谓：太极生两仪，两仪生四相，四相生八卦...所以最简单的就是最易用的，也是速度最快的。

扯远了，具体算法明细可参照微软官方解释Microsoft Naive Bayes 算法

因为对于上两篇中的应用场景，对买自行车的顾客群体进行预测，贝叶斯算法同样也可以做到，反而更简洁，本篇咱们使用这种算法来预测下，并且看看这种算法它的优越性有哪些。

技术准备

（1）同样我们利用微软提供的案例数据仓库（AdventureWorksDW2008R2)，两张事实表，一张已有的历史购买自行车记录的历史，另外一张就是我们将要挖掘的收集过来可能发生购买自行车的人员信息表，可以参考上一篇文章

（2）VS、SQL Server、 Analysis Services没啥可介绍的，安装数据库的时候全选就可以了。

---

下面我们进入主题，同样我们继续利用上次的解决方案，依次步骤如下：

（1）打开解决方案，进入到“挖掘模型”模板

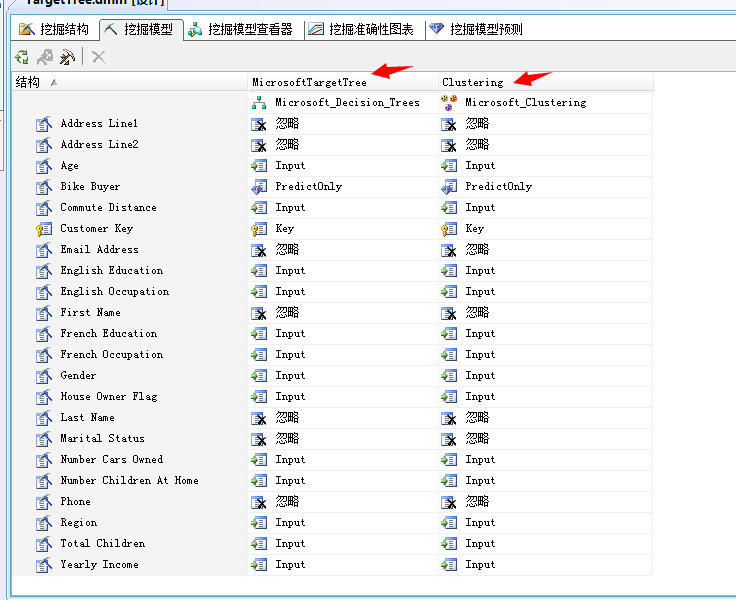
可以看到数据挖掘模型中已经存在两种分析算法，就是我们上两篇文章分析用到的决策树分析算法和聚类分析算法。我们继续添加贝叶斯算法。、

2、右键单击“结构”列，选择“新建挖掘模型”，输入名称即可

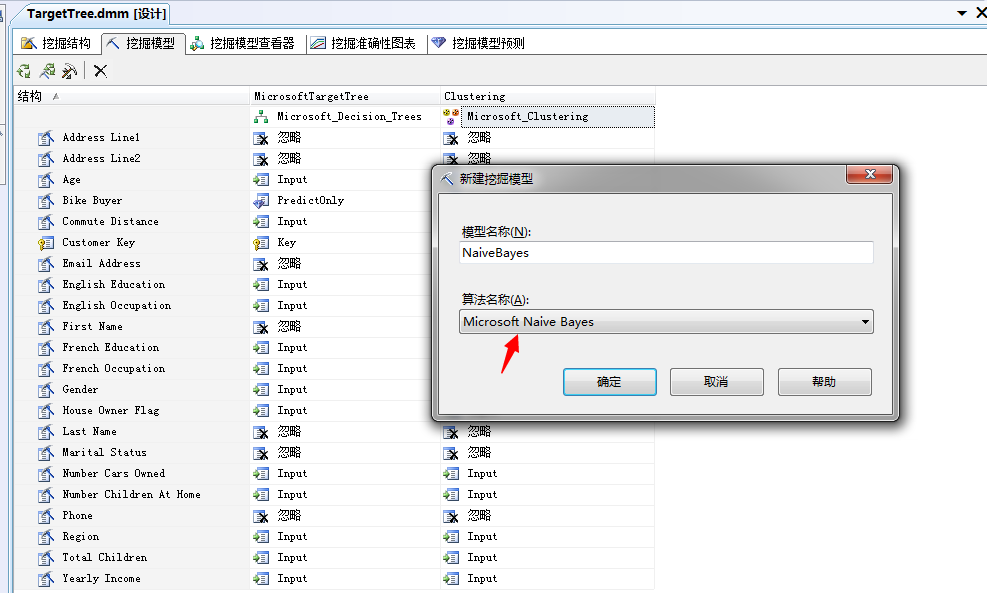
点击确定，这时候会弹出一个提示框，我么看图：

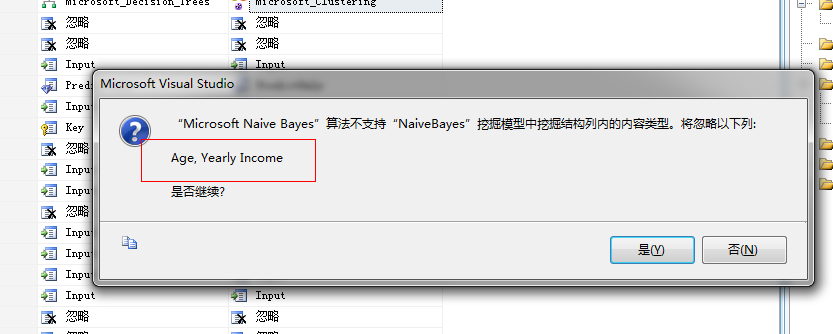
啥子意思？....上面我们已经分析了贝叶斯算法作为最简单的两元状态预测算法，对于离散值或者连续值它是无能为力的，它单纯的认为这个世界只有两种状态，那就是是或者非，上图中标识的这两列年龄、年收入很明显为离散的属性值，所以它是给忽略的。点击“是”即可。

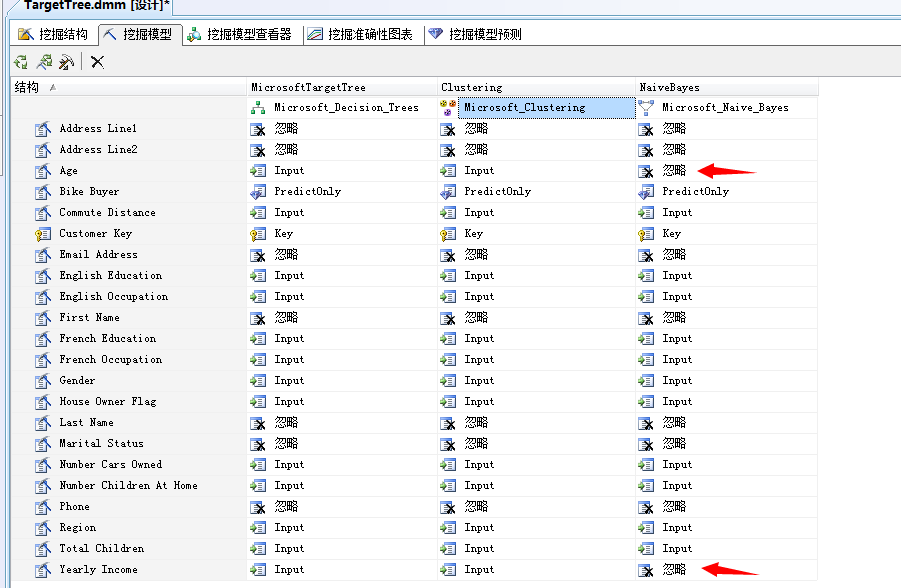
这样我们新建立的贝叶斯分析算法就会增加在挖掘模型中，这里我们使用的主键和决策树一样，同样的预测行为也是一样的，输入列也是，当然可以更改。

下一步，部署处理该挖掘模型。

---

结果分析

同样这里面我们采用“挖掘模型查看器”进行查看，这里挖掘模型我们选择“Clustering”，这里面会提供四个选项卡，下面我们依次介绍，直接晒图：

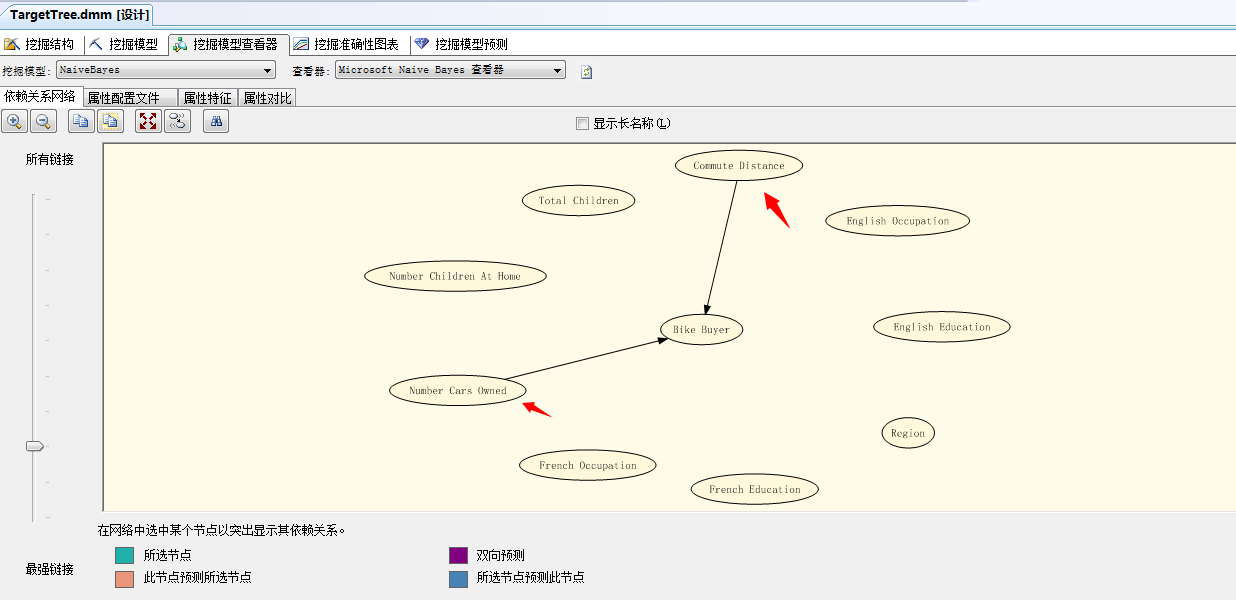
这个展示面板可爱多了，集中了决策树算法中的“依赖关系网络”，聚类算法中的“属性配置文件”、“属性特征”、“属性对比”；同样也是这种算法的优点，简单的特征预测，基于对立面的结果预测，但也有它的缺点，下面我们接着分析：

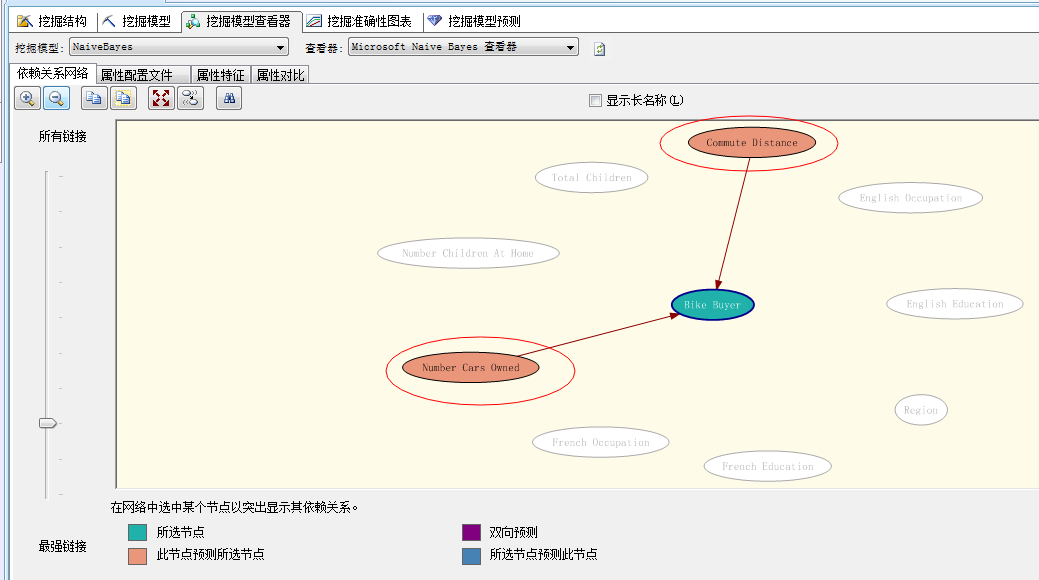
从依赖关系网络中可以看到，现在影响购买自行车行为的依赖属性最重要的是“家庭轿车的数量”、其次是“通勤距离”....当年我们通过决策树算法预测出来的最牛因素“年龄”，现在已经没了，汗...只是因为它是离散型值，同样年收入也一样，这样其实使得我们算法的精准度会略有偏低，当然该算法也有决策树算法做不到的，我们来看“属性配置文件”面板：

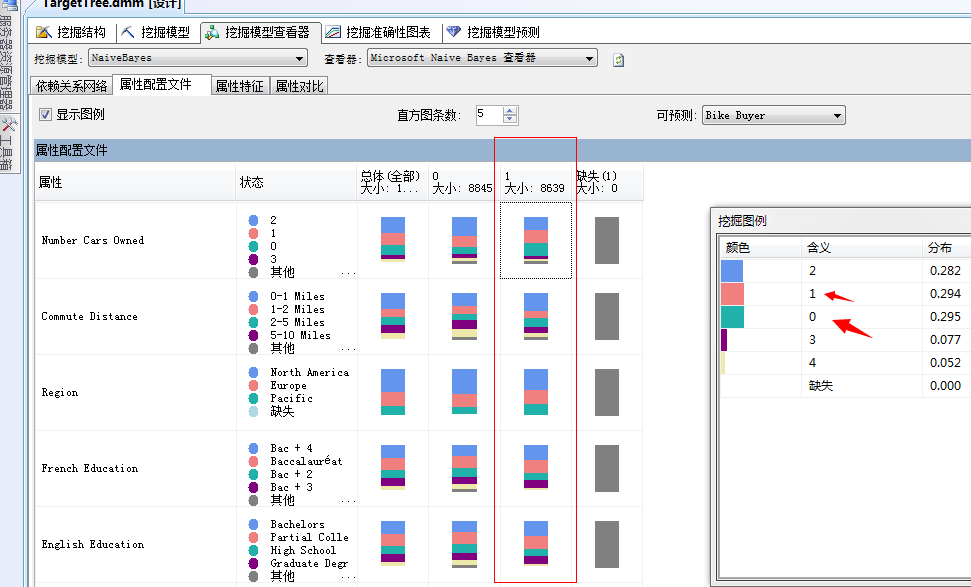
通过该面板我们已经可以进行群体特征分析，这一点是决策树分析算法做不到的，当然这是聚类分析算法的特点，上面图片中含义就能看到了家里有1个或者没有小汽车购买自行车的意愿更大一点。其它的分析方法类似，具体可以参照我的上一篇聚类分析算法总结。

“属性特征”和“属性对比”两个面板结果分析也是继承与聚类分析算法一样，上一篇文章我们已经详细介绍了，下面只是切图晒晒：

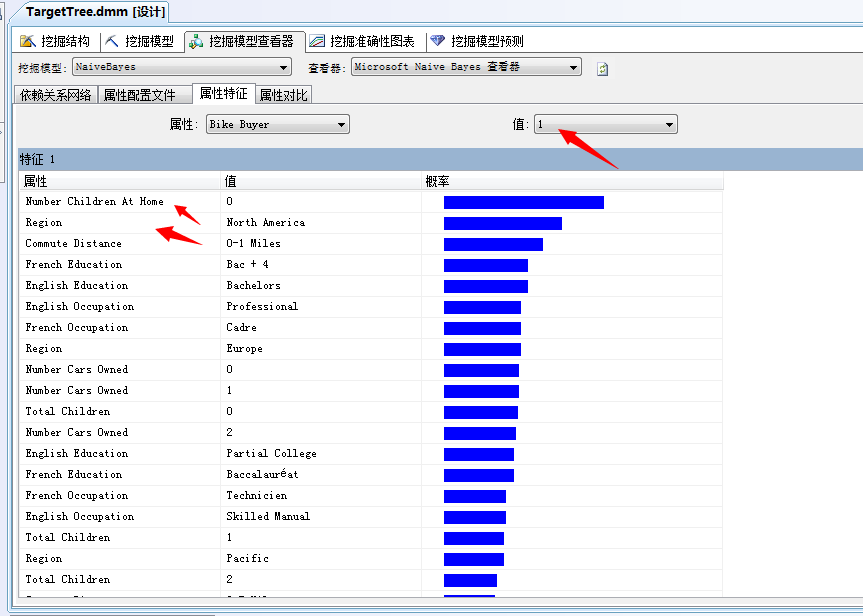
是吧，家里没有孩子、在北美的、一般行驶距离在1Miles(公里？)以内的同志比较想买自行车。

家里没有小汽车...通常会买自行车倾向于1，如果有2辆了基本就不买了倾向于0,汗...常识...其它就不分析了。

下面我们看一下这种算法对于咱们购买自行车群体预测行为的准确性怎么样

---

准确性验证

最后我们来验证一下今天这个贝叶斯分析算法的准确性如何，和上两篇文章中的决策树算法、聚类分析算法有何差距，我们点击进入数据挖掘准确性图表：

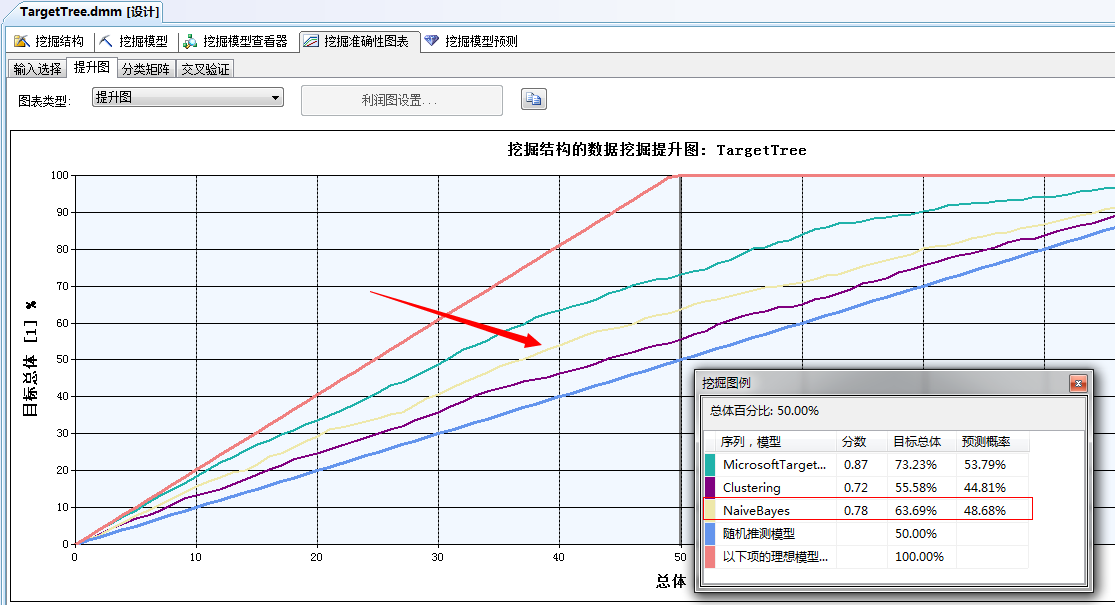
可以看到，此次用的贝叶斯分析算法评分已经出来了，仅次于决策树算法，依次排名为：决策树分析算法、贝叶斯分析算法、聚类分析算法。看来简单的贝叶斯分析算法并不简单，虽然它摒弃掉了两大属性值：年龄、年收入，而且其中年龄属性通过决策树分析算法分析还是比较重要的一个属性，贝叶斯无情的抛弃之后，依然以0.78分的优势远远胜于聚类分析算法！而且上面的分析可以看到它还具有聚类分析算法特长项，比如：特征分析、属性对比等利器。

到此通过三种分析算法的评比，我们好像已经看到了适合我们这种应用需求的最优的分析算法，每种算法的评比，通过上的曲线图已经轻易的展现出来来了，当然咱们今天的这篇Miscrosoft贝叶斯分析算法也应该结束了。

<------------------------------------------------------------华丽分割线------------------------------------------------------------------------------------------>

但是.......我记得上次写聚类分析算法的时候，我无意间提到过，如果将国内IT从业人员和非IT从业人员根据性别属性进行预测的话...结果将会是不寒而栗！你懂得，那我们推测下这里买不买自行车会不会也与性别有关呢？通常男孩子比较喜欢骑自行车...嗯..我是说通常...那么结果呢...我们来看：

我们利用上图中打分最高的决策树分析算法来推测我们的问题，我们在”挖掘模型”中右键选择新建模型，选择决策树分析算法，我们起个名字：

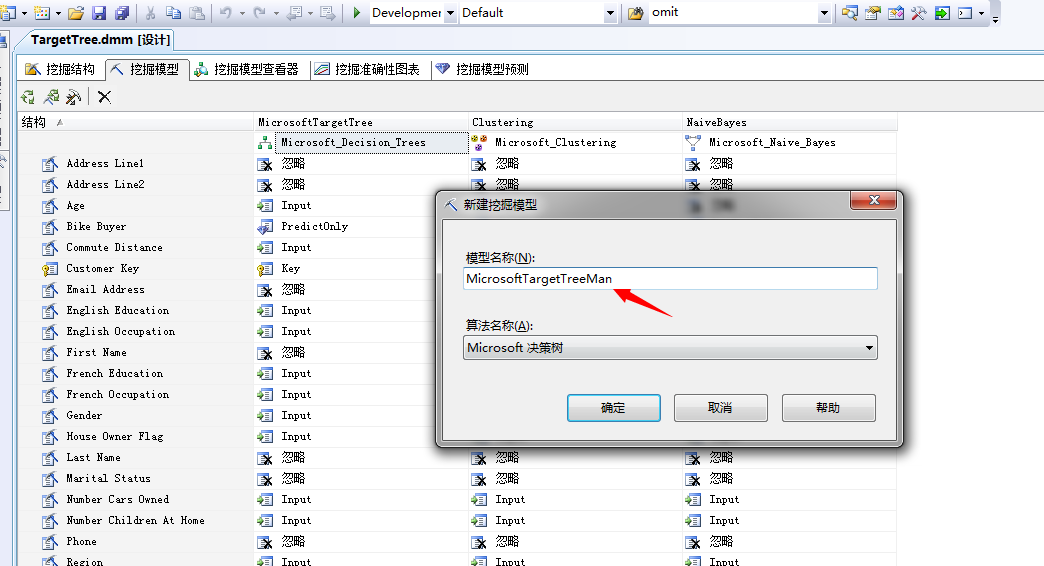
点击确定，我们已经将使用决策树分析算法分析男性购买自行车的概率，然后在该算法结构上右键，选择“设置模型筛选器”。我们来设置筛选过滤条件为：M，即为男银

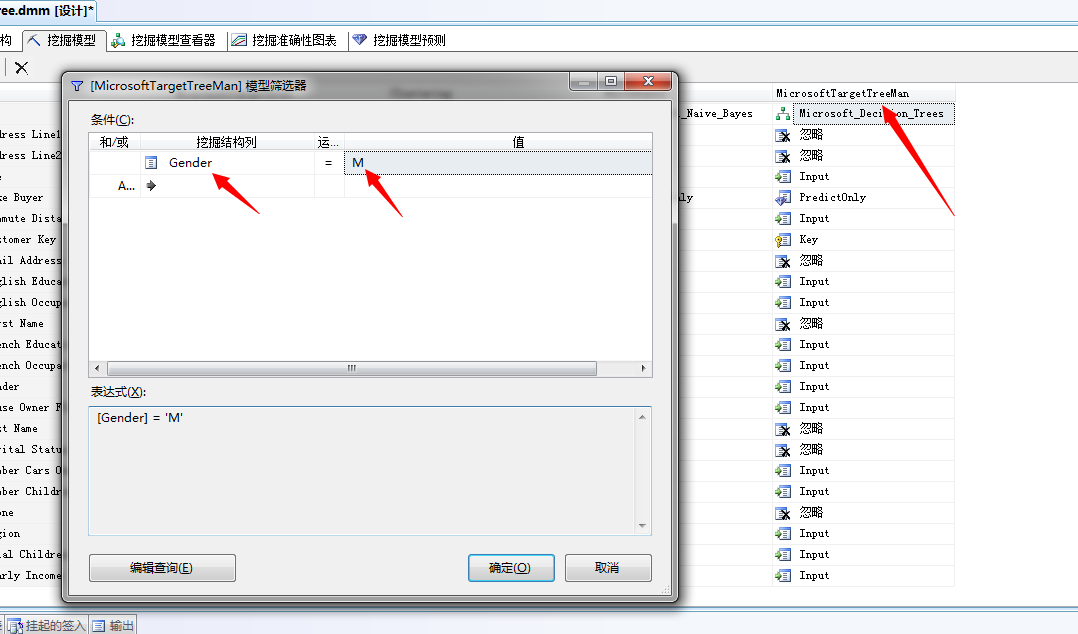
我们利用想用的方法继续建立women(女银)的决策树挖掘算法，下面看图：

这里就不不过多解释了，我们直接验证结果，来看看我们上面的推断有没有意义。

下面看图：

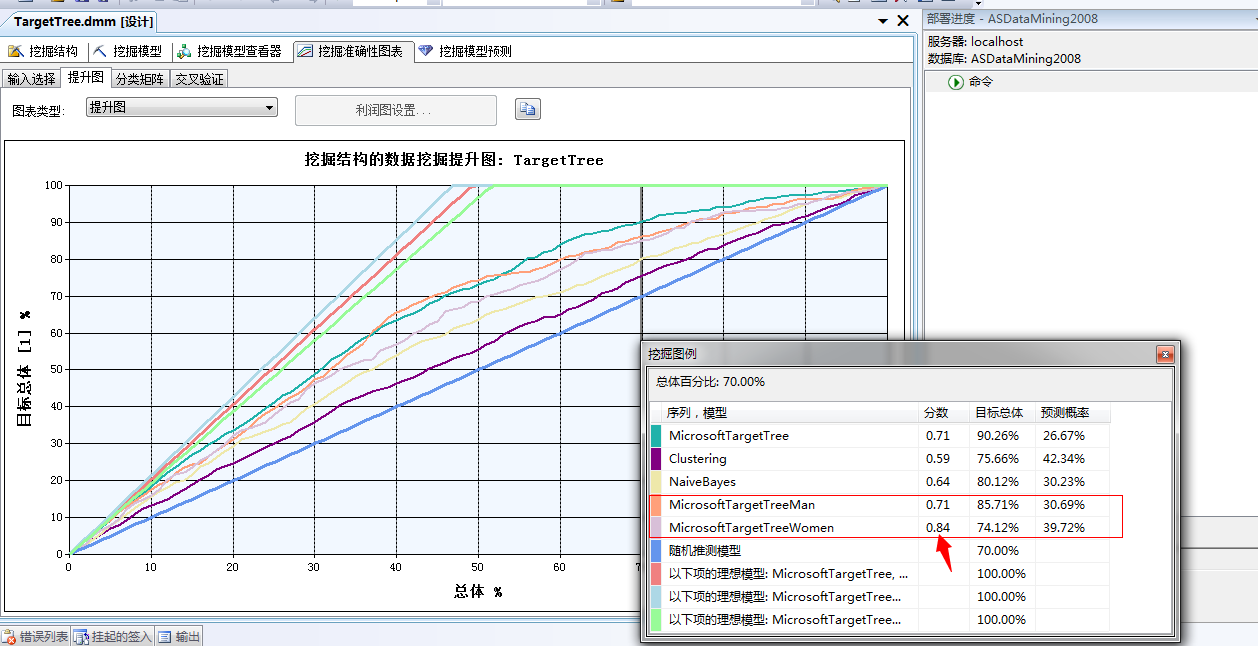
....额...额...e...表激动...我那个去...上面根据性别的进行区分的预测模型结果已经出来了，从打分上看，Man(男银)的决策树已经能和全部的事例结果相聘美，都是0.71...这也就是说明我们只需要对男人的群体进行预测就可以得到全部市场的规律..而不需要花费精力去研究全部......但是Women(女银)的分数直接飙升到0.84....汗...在这几种挖掘算法中利用决策树算法对于Women这个群体进行预测，结果的精准度竟然达到如此之高！这个模型的存在直接秒杀了其它的任何一种分析算法，神马聚类、贝叶斯都是浮云....浮云而已。

通过上面的分析，我们已经确立了我们的推断，男性和女性同志在想不想购买自行车这件事情上是有群体差异的，并不是只通过分析全部的事实就可以得到，当然本身而言就男性和女性这两种地球上特有的物种在行为和特征上就有较大的差距，对于买不买自行车当然也不会相同，呵呵...至少大米国是这样，上面的图表验证这一说法！所以对于不同的行为预测我们可以针对性别来分别挖掘，这样我们挖掘后得到的推测值将更接近事实。

有兴趣可以对是否结婚两种群体进行分析挖掘，看看结不结婚和买不买自行车有没有关系。

本问建模来自：（原创）大数据时代：基于微软案例数据库数据挖掘知识点总结（Microsoft Naive Bayes 算法）