H5系列之canvas

what is canvas？(什么是canvas)

其实他只是H5里面的一个标签而已，那么他作为一个标签，肯定有他的用途，他就像是一幅画布，等待着你来作画。可以说，他只是一个容器而已，需要配合着JavaScript来进行绘制。

那么他能做些什么东西呢？

例如这个：http://www.yyyweb.com/demo/tearable-cloth/index.html

还有这个：http://canvasrider.com/tracks/409068

用处很多，但是用的最多的还是，简单的画个图形啊，图形移动什么的。

　　画三角形

画矩形

　　画圆

　　画圆角矩形

　　填充颜色

　　图形缩放，平移与旋转

　　填充图片

那么开始介绍它的怎么使用的：

创建标签，那么画布的大小设置，在标签上面设置，如果在css设置，设置的是这个标签的大小，而不是画布的大小，这点要注意。

<canvas width="500px" height="500px"></canvas>

<canvas width="500px" height="500px" style="border: 1px solid"></canvas>

加上边框，以便于我们知道他在哪里，下面的框框，就是画布的区域了

开始准备工作 ↓

<body>

　　<canvas id="can" width="500px" height="500px" style="border: 1px solid"></canvas>

<script>

　　var can = document.getElementById('can'); //选择canvas标签

　　var ctx = can.getContext('2d'); //选择画布的绘制的类型，只能填2d

</script>

</body>

开始画出我们的第一条线。

 <script>

    var can = document.getElementById('can');

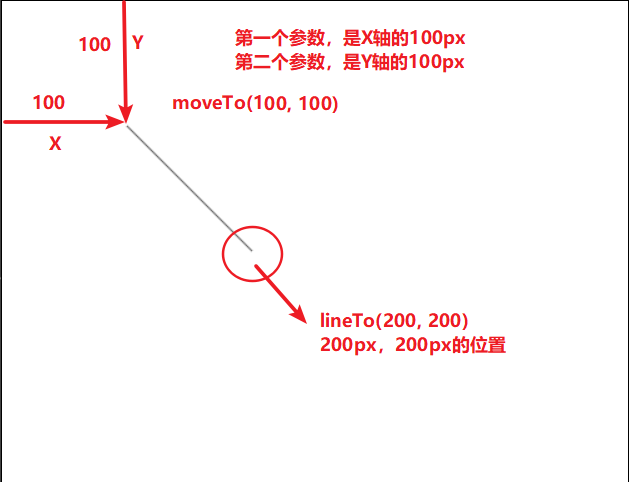
    var ctx = can.getContext('2d');           

    ctx.moveTo(100,100);    // 选择在画布中的起始位置， 左上角是0，0

    ctx.lineTo(200,200);    // 选择从起始位置开始，画到 200 200 的位置

    ctx.stroke();           // 开始画。

</script>

<script>

    var can = document.getElementById('can');

    var ctx = can.getContext('2d');           

    ctx.moveTo(100,100);

    ctx.lineTo(200,200);

    ctx.lineTo(0, 200); //再添加一条线

    ctx.stroke();           
</script>

效果图如下：

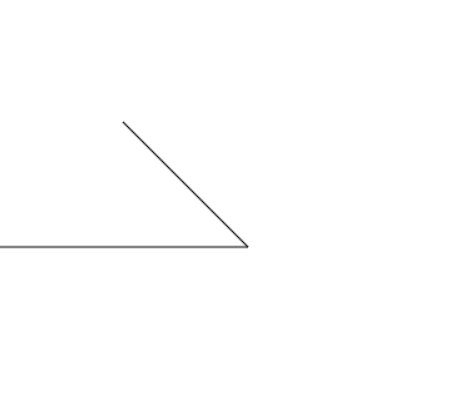
接下来，闭合他形成一个三角形

<script>

    var can = document.getElementById('can');

    var ctx = can.getContext('2d');           

    ctx.moveTo(100,100);

    ctx.lineTo(200,200);

    ctx.lineTo(0, 200);

    ctx.closePath();//闭合图形，有两条线以上的，能自动帮你连接到 起始点。

    // ctx.lineTo(100,100)；当然自己计算位置，也是可以的

    ctx.stroke();

 </script>

效果图如下：一个三角形的形状就出来了。

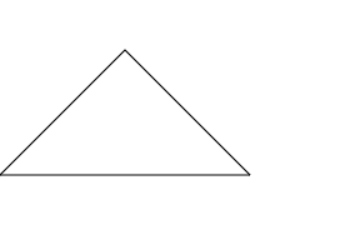
上面是画直线，下面画曲线。画曲线呢，需要用到二次贝赛尔曲线，和三次贝赛尔曲线。

二次贝塞尔曲线呢，有三个点。起始点，控制点，和终点。首先，现象一个常见。有一条绳子，头尾固定，在中间再绑一条绳子，往上拉。就像下面这样

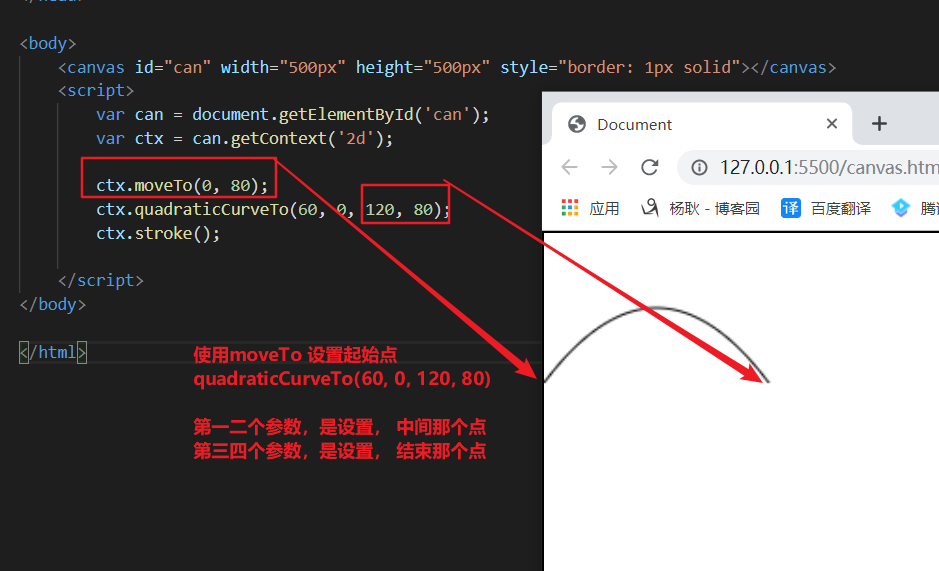
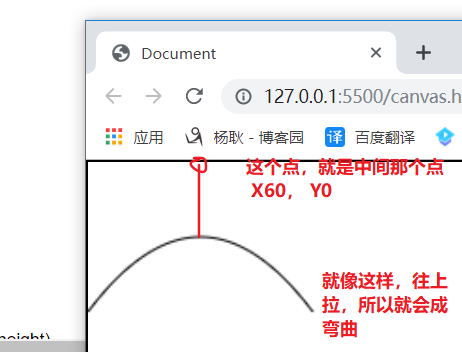
所以中间那个点，如果越高，那么就会越弯曲。

那么还有个三次贝塞尔曲线，听名字就知道，比二次贝赛尔曲线多了一个点。bezierCurveTo()

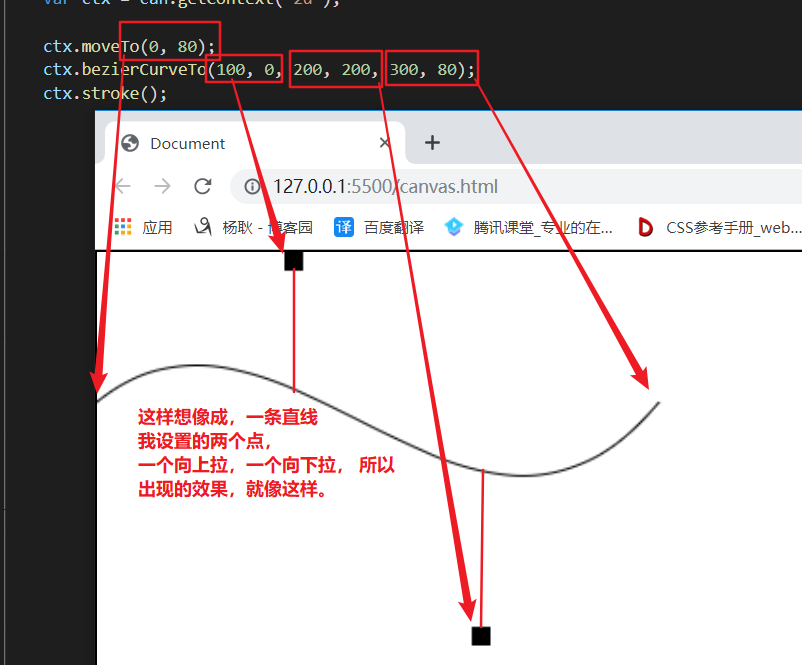
接下来画个矩形吧。

画矩形呢，不需要一步一步的画，有方法，直接可以画 cxt.rect(x,y,width,height)

<script>

    var can = document.getElementById('can');

    var ctx = can.getContext('2d');           

    ctx.rect(50, 50, 200, 100); //第一二个参数是  起始点的X，Y，第三四个参数是 矩形的宽高

    ctx.stroke();       //开始画

</script>

效果如下：

不过，不止有一个方法而已，还有另外两个方法：

<script>

        var can = document.getElementById('can');

        var ctx = can.getContext('2d');           

        ctx.strokeRect(50, 50, 200, 100); //第一二个参数是  起始点的X，Y，第三四个参数是 矩形的宽高
　　　　　//不用写 ctx.stroke（）；


    </script>

这个方法的，虽然也是画矩形，只不过他会填充颜色。

<script>

    var can = document.getElementById('can');

    var ctx = can.getContext('2d');           

    ctx.fillRect(50, 50, 200, 100); //第一二个参数是  起始点的X，Y，第三四个参数是 矩形的宽高

</script>

接下来，画圆。arc(100，100，50，0，Math.PI *2, 0), 第一二个参数，还是起始点的位置X，和Y。只不过起始点是在圆心。第三个参数是，圆的半径，第四五个参数，是起始弧度的位置，和结束的位置，最后一个参数，是以顺时针，还是逆时针画 0为顺时针，1为逆时针。

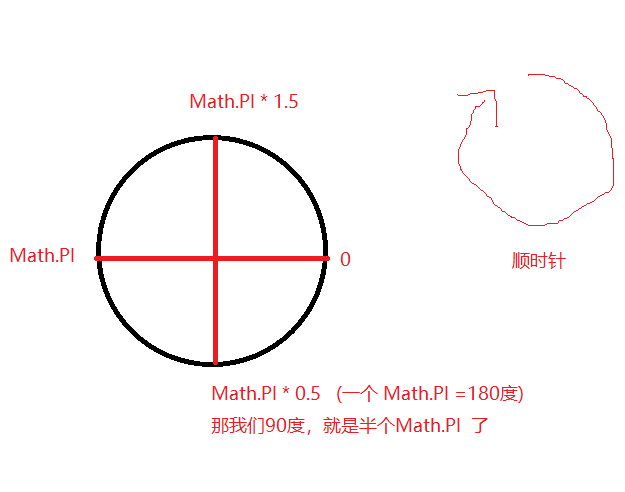
那我们设置，第四个参数，为0，第五个参数为360度，也就是 Math.PI * 2。是不是就是一个圆啦。

<script>

    var can = document.getElementById('can');

    var ctx = can.getContext('2d');           

    ctx.arc(100, 100, 50, 0, Math.PI *2, 0);

    ctx.stroke();

</script>

还有一个注意点，顺时针的，90度，和逆时针的90度，是不一样的呢。

ctx.arc(100, 100, 50, 0, Math.PI *0.5, 0);

ctx.arc(300, 100, 50, 0, Math.PI *0.5, 1);

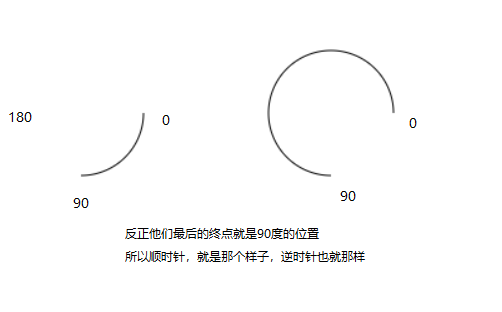
再画个圆角矩形。需要用到arcTo()方法，首先，我们需要知道几个点的位置 ↓

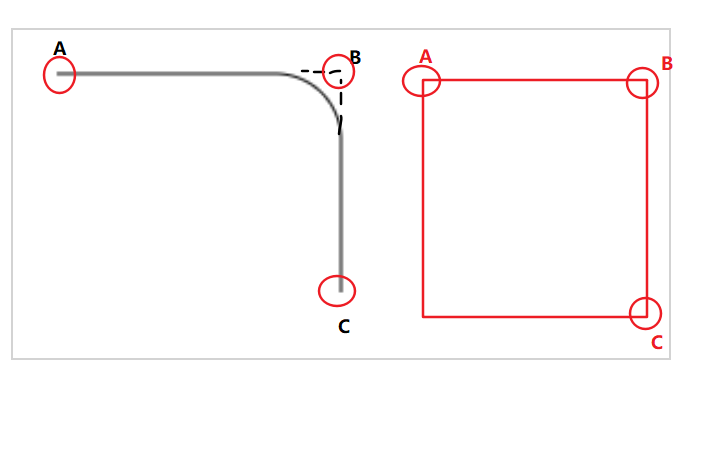
arcTo(150, 20, 150, 30, 50)呢，有5个参数, 第一二个参数，是决定了 B点的位置，第三个四个参数呢，是决定了怎么弯，往上弯，还是往下弯。第五个参数呢，是圆角的像素，像border-radius 属性一样。

第一步，决定A点，使用moveTo(20, 20)。

ctx.moveTo(20, 20);

第二步，决定B点的位置。

ctx.arcTo(150, 20, , , ,);

第三步，往上弯，还是往下弯(这个属性怎么决定呢？第三个参数，可以理解为X，B点的X为150，你如果要往上下弯的话，那么第三个参数，就要跟B点的X 一样。也就是150，

关键在第四个值，第四个参数，是Y，如果要往下弯的话，那么Y的值，就要大于 B点的Y值，如果要往上弯的话，就要小于B点的Y值。大多少小多少无所谓，只要大过就行)

ctx.arcTo(150, 20, 150, 30, );

第四步，决定角度的程度

ctx.arcTo(150, 20, 150, 30, 50);

第五步，画出来

ctx.stroke();

效果图：

如果要往上弯呢，第四个参数要小于 B点的Y 对吧。那么我们把代码改成 ctx.arcTo(150, 20, 150, 10, 50); 第四个参数 10，比B点的Y 20 小。所以会变成往上弯。

记住一点就行。(如果要往上下弯，改变Y，往左右弯，改变X)

那么接下来，画个完整的圆角矩形。

这是我们上面教的。到这里应该怎么办了呢。计算出 A点的 X 和 Y等于200，80

最后一个点。

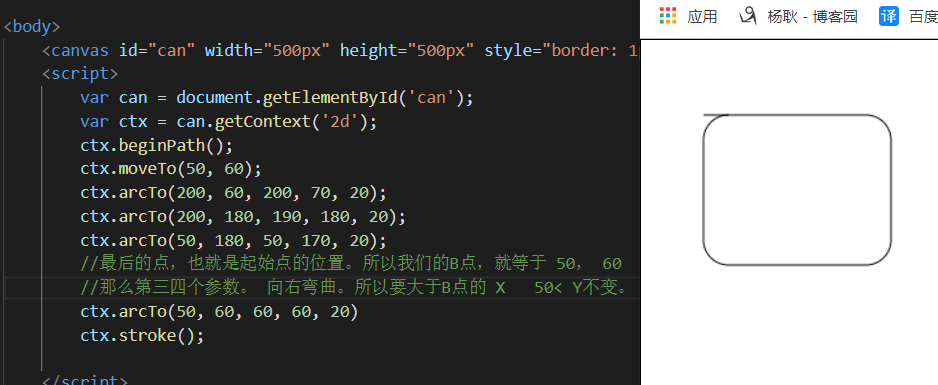
最后，会发现，出了一条线。我们只需要把起始点的X +20 即可。为啥+20？因为弯曲的值为 20。

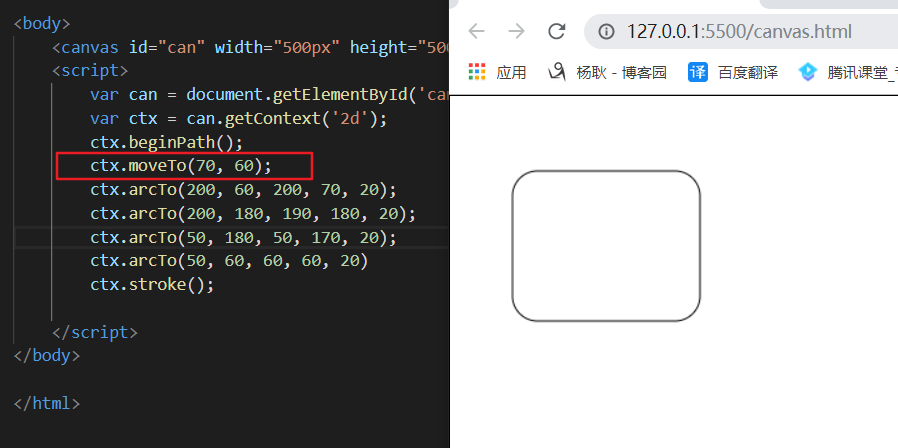
给画好的图形填充颜色。

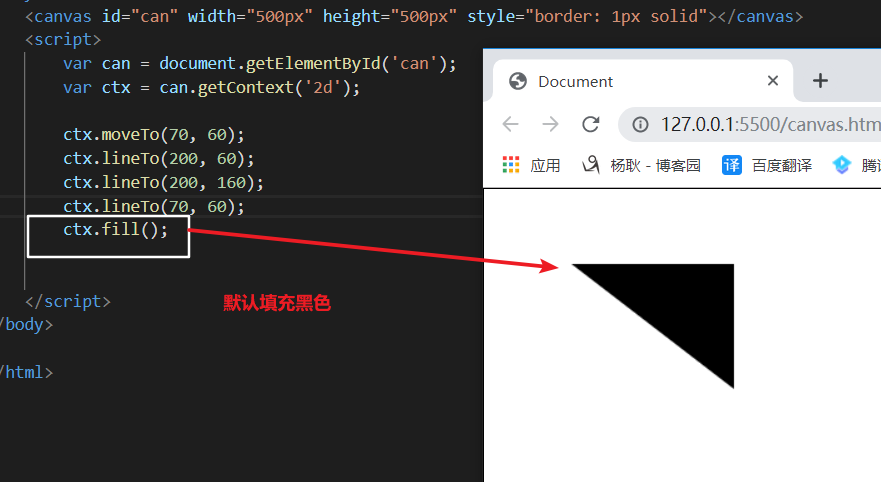
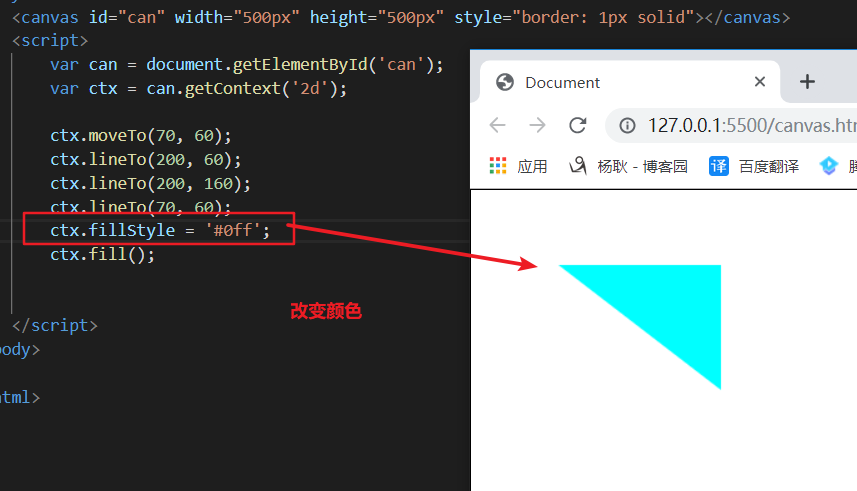
其实他还不止可以填充单色。还可以填充线性渐变，径向渐变。

线性渐变：

createLinearGradient() 怎么理解呢。你可以把它理解为，这个要填充的矩形。

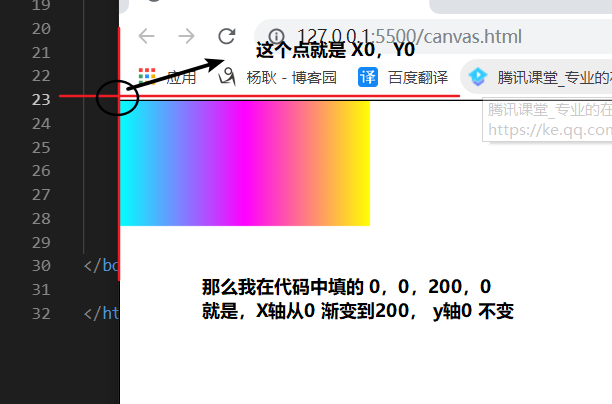
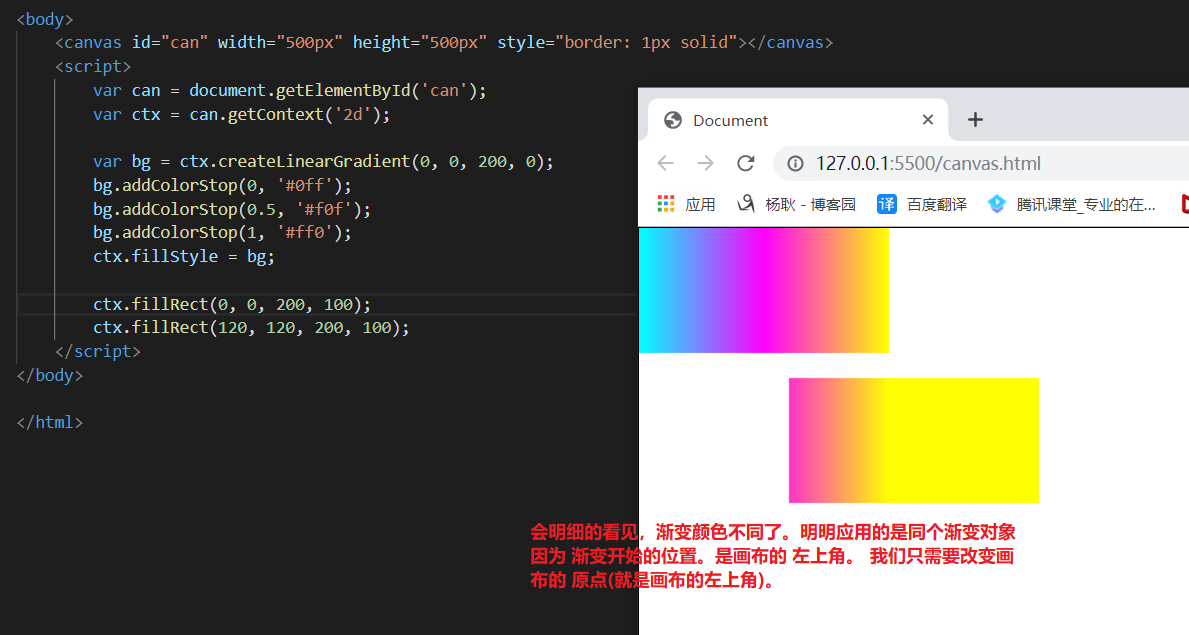
因为，渐变开始的点，是X0，Y0，并不是图形的左上角那个点，而是画布的左上角 (原点) 所以，你把图形的位置移动一下。你就会发现问题了。

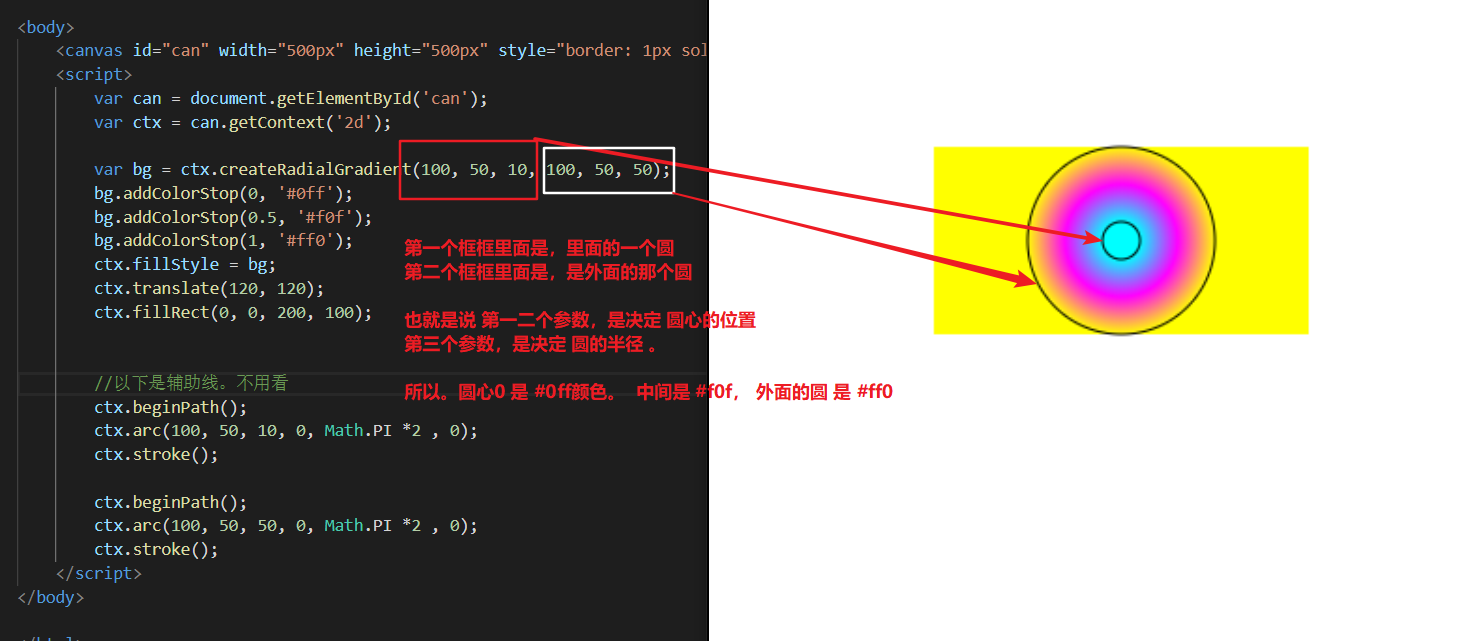
有没有想过一个问题，如果内圈的圆，超过外面的圆会成什么样子？

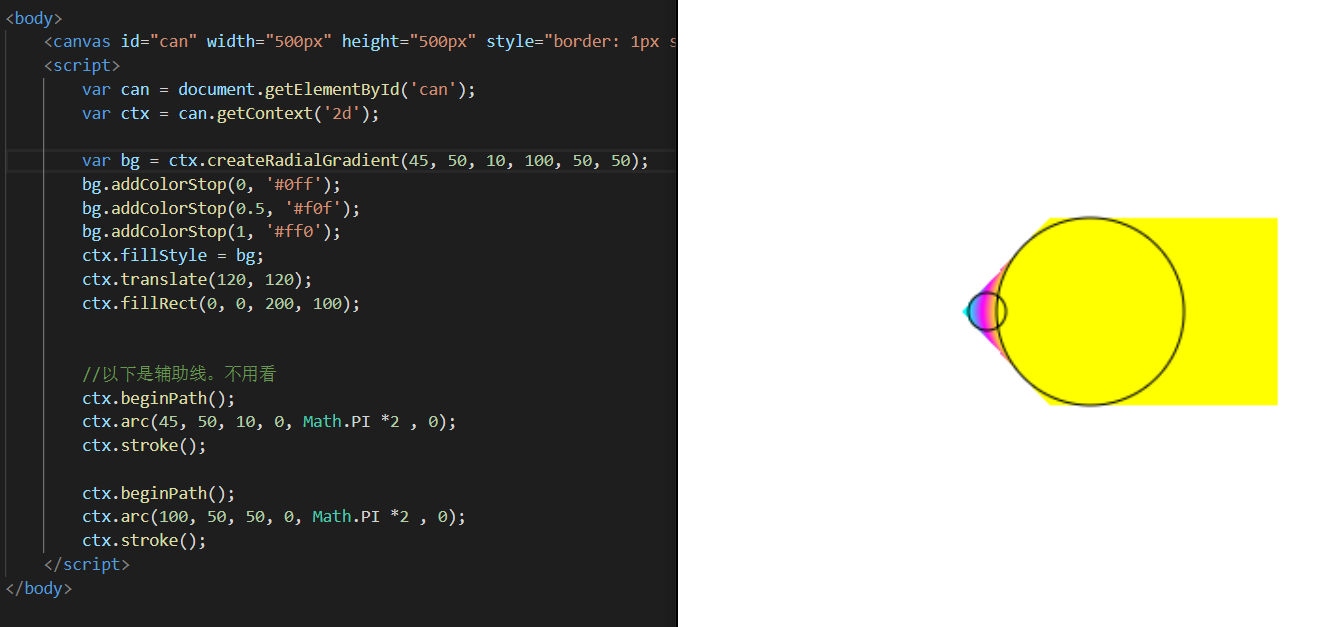
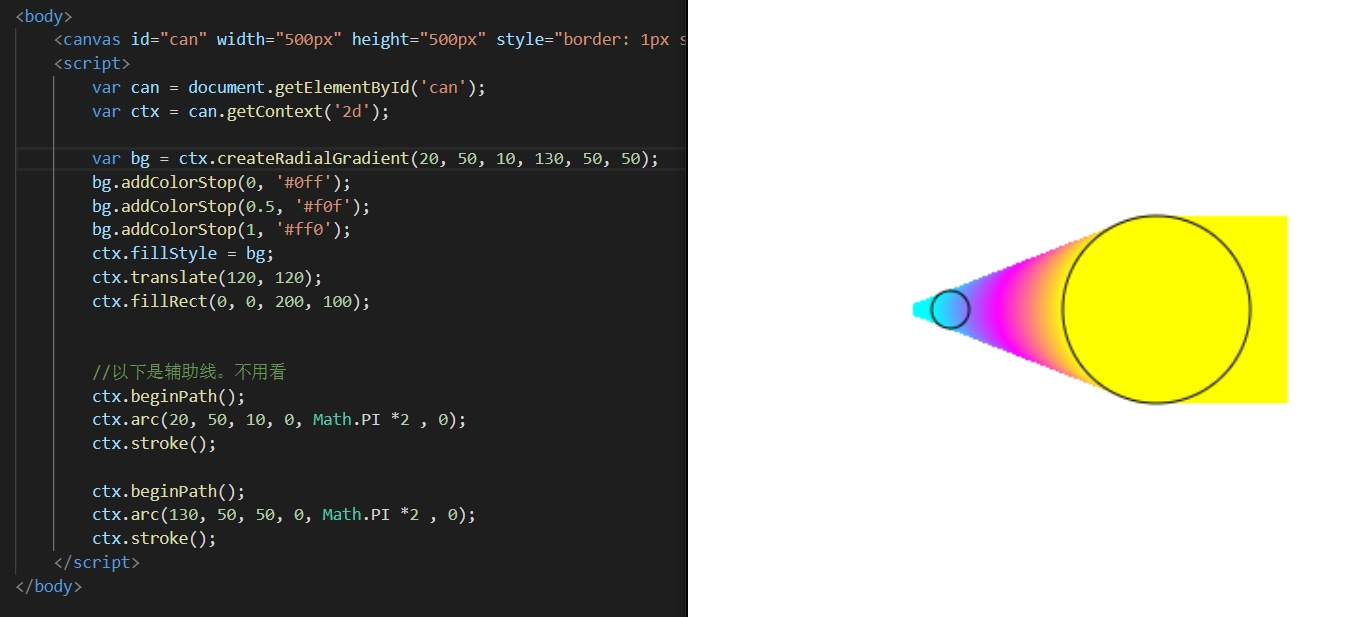
如果两个圈，相等且相离呢？

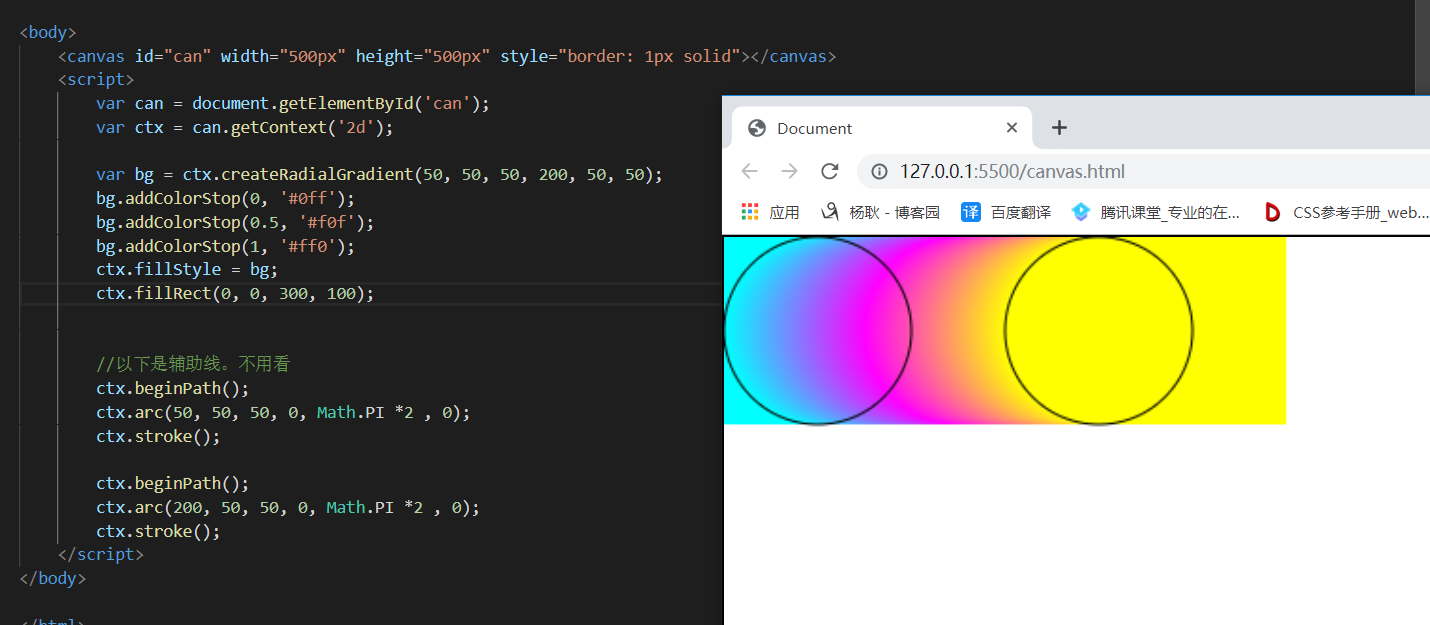
话说，为什么会出现这种情况呢？其实最主要的一点还是，他的原理，下面是一张原理示意图：

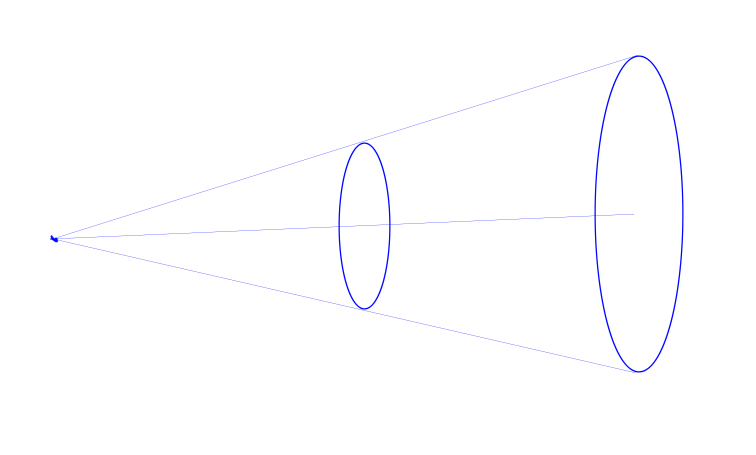
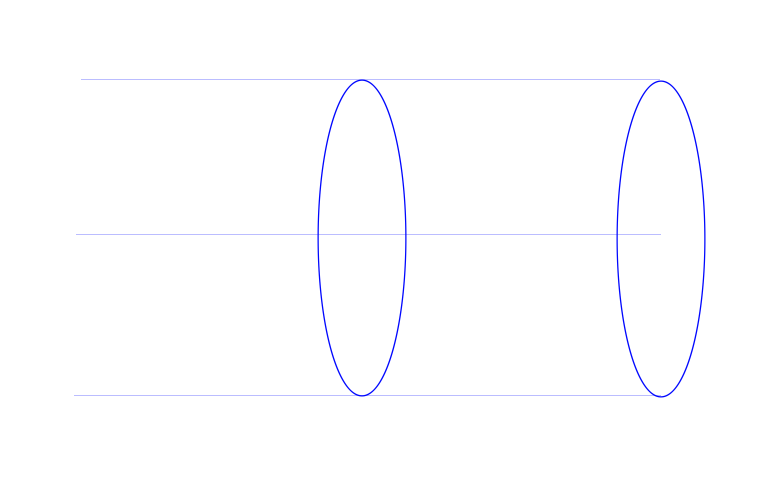
现在，我们会画单个图形了，如果要画多个图形，或者，多条线，不相连呢？因为我们知道，我们的每一笔操作，都是连在一起的。

有个方法。ctx.beginPath()。可以把它理解为，我把笔拿起来。具体下个位置在哪里。需要再次重新定起始点。

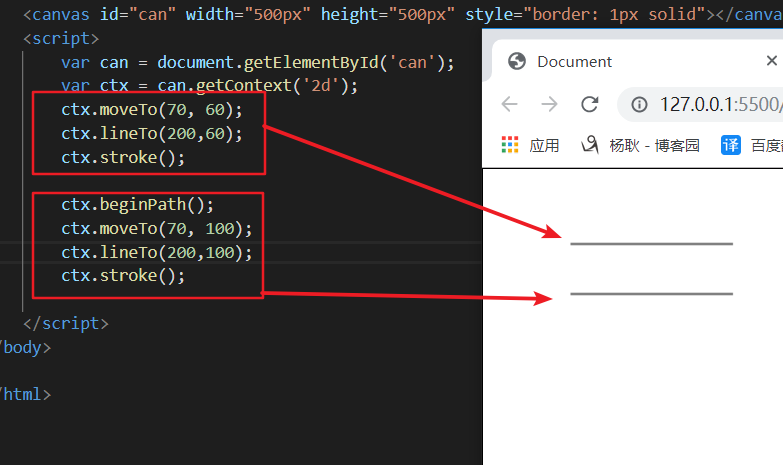
如果不把笔拿起来会怎么样呢？ ↓ 像写连笔字一样，不会中断的。

如果要画两个图形，或者不连在一起的话，需要使用beginPath() 方法。可以重新设置起始点。

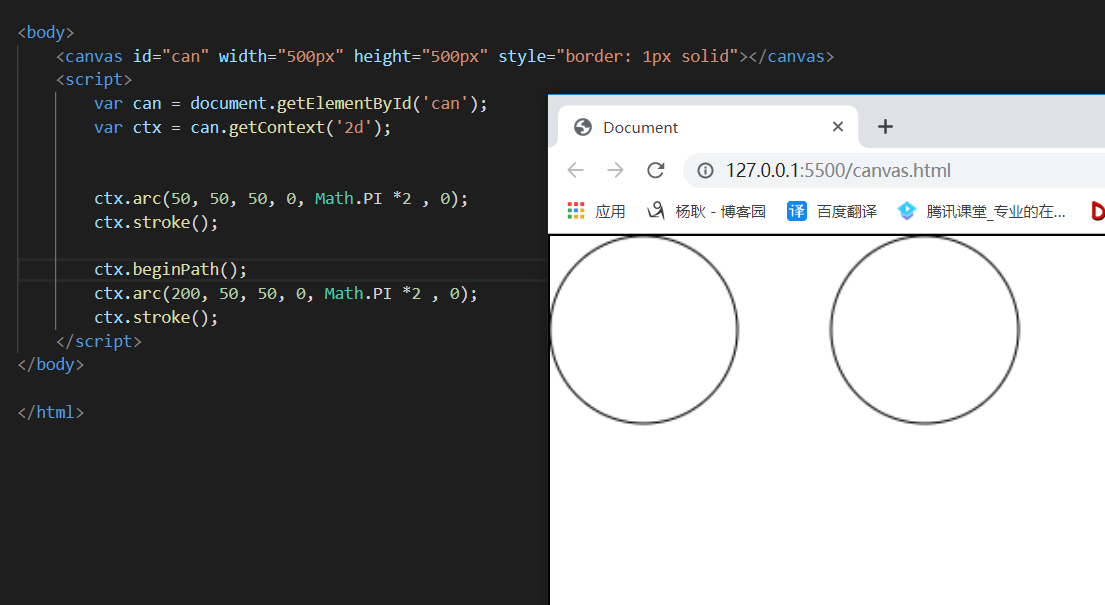
缩放，平移，旋转

缩放ctx,scale(1, 1); 1是默认值，正常大小。小于1 也就是 0~0.99 都是缩小，大于1呢 2是2倍， 3是3倍。如此类推

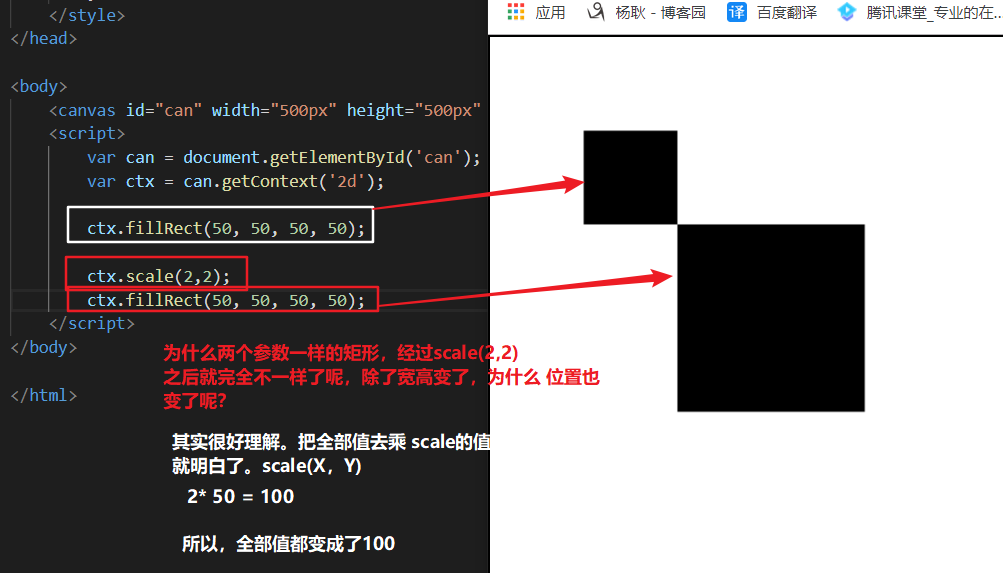
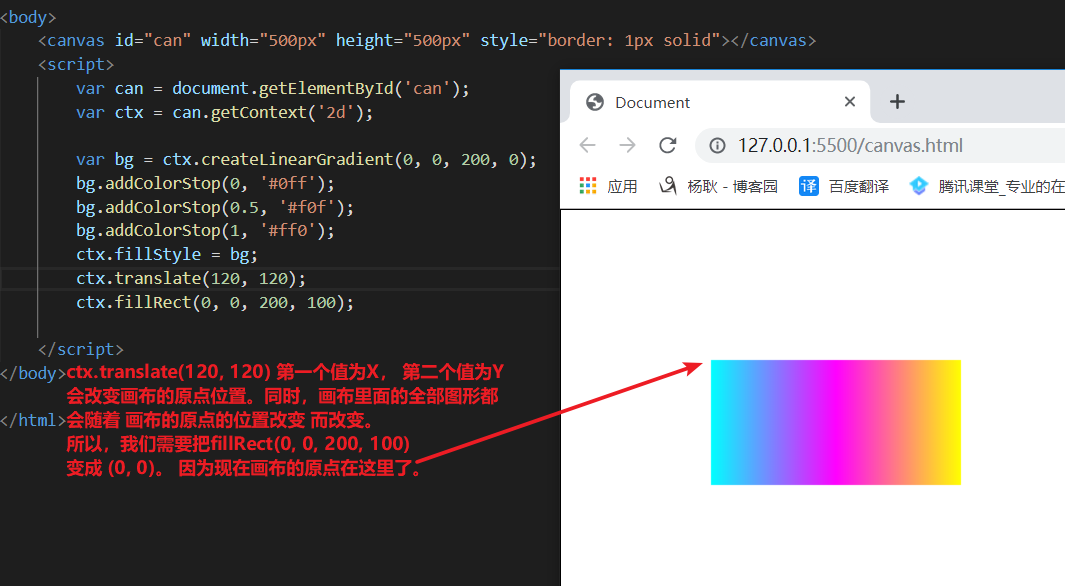
平移。ctx.translate(100, 100);

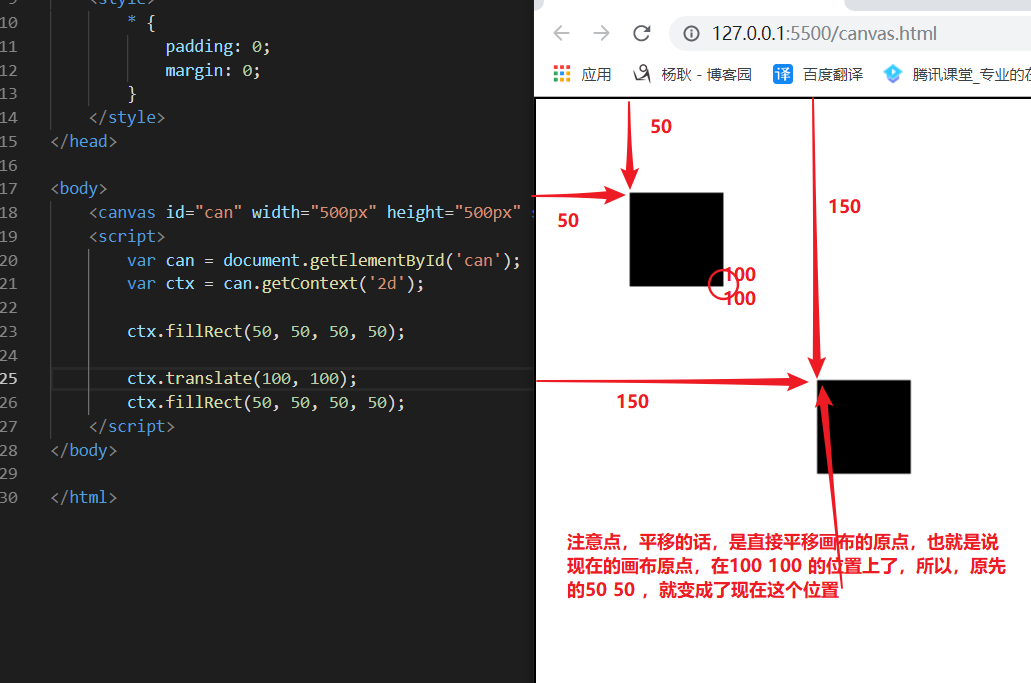
旋转。ctx.rotate(Math.PI) 一个PI 等于180度，以画布原点旋转，而不是以自身的左上角旋转。

如果要把旋转点，在图形上面，是用translate 进行平移原点即可。

那么缩放，平移，旋转，都是按照原点进行的，后续的操作，都会受到原点的移动，而发生错位，什么的。所以canvas 还有一个方法，就是用来存储数据的。

那么，如何不受到影响呢？使用ctx.save() 方法进行存储画布原点的位置。

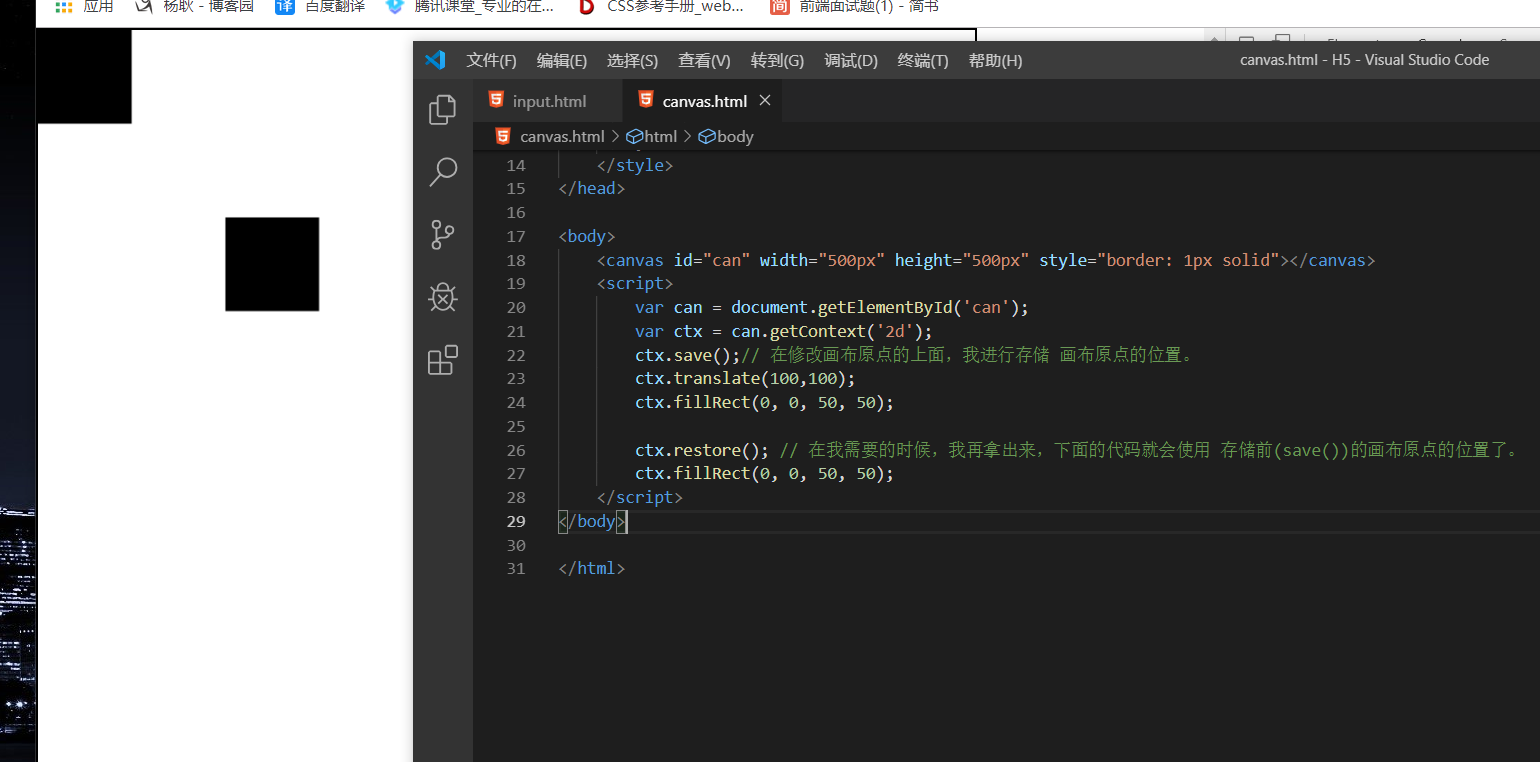
那么 save 能存储什么呢？他能存储 translate rotate scale 的值。因为这些改变，都是全局的。

接下来，把图片放进canvas 画布里面。

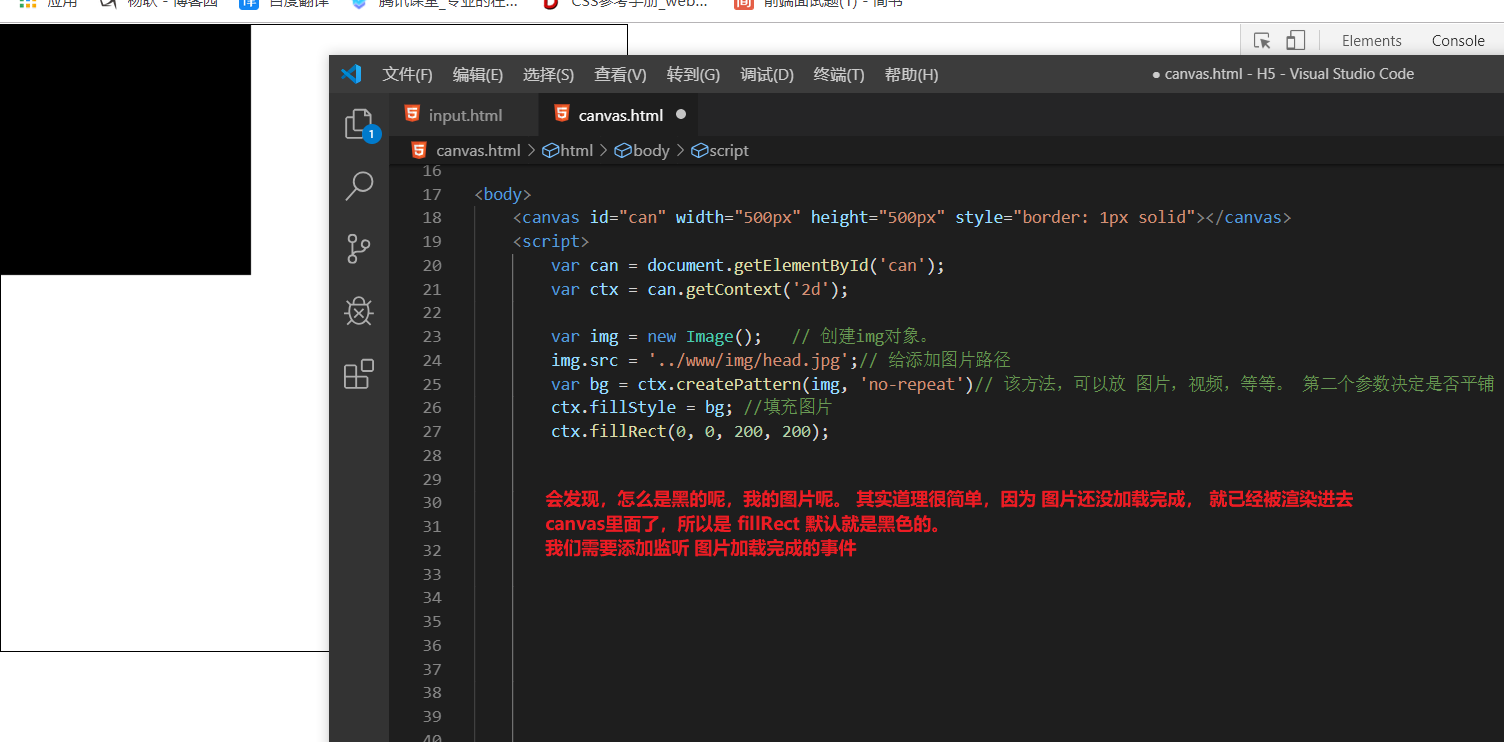
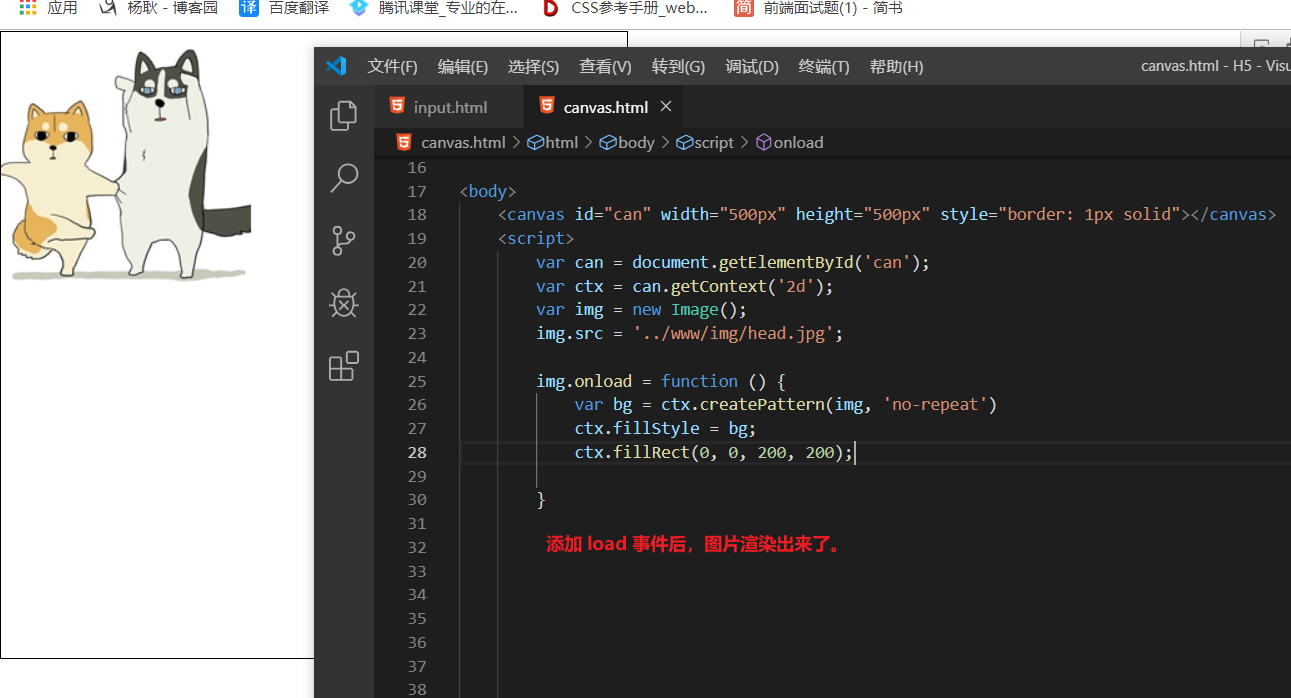
还有另外一种填充图片的方法：

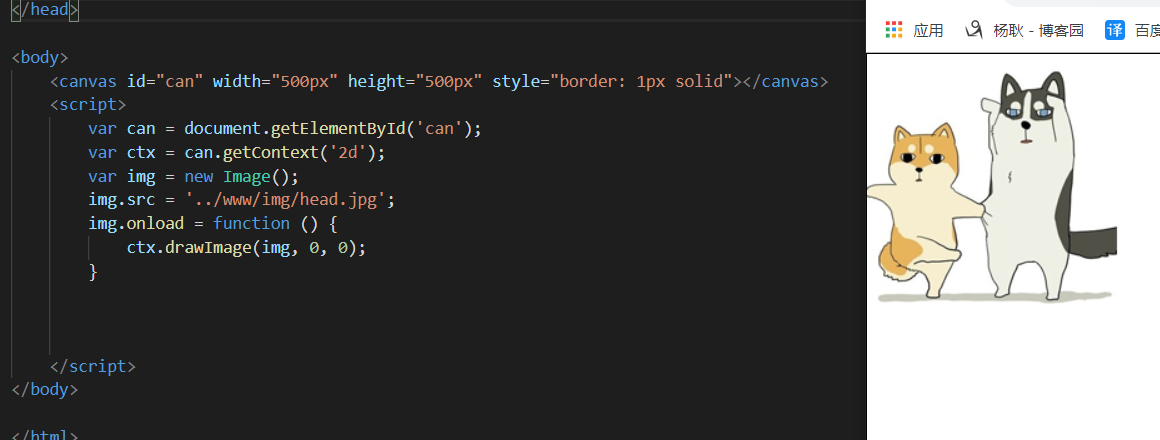
drawImage方法，可选参数：

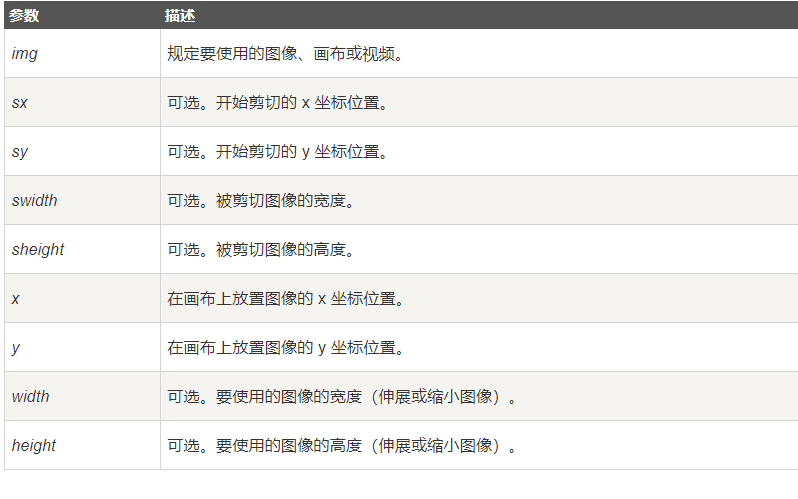
填充文字

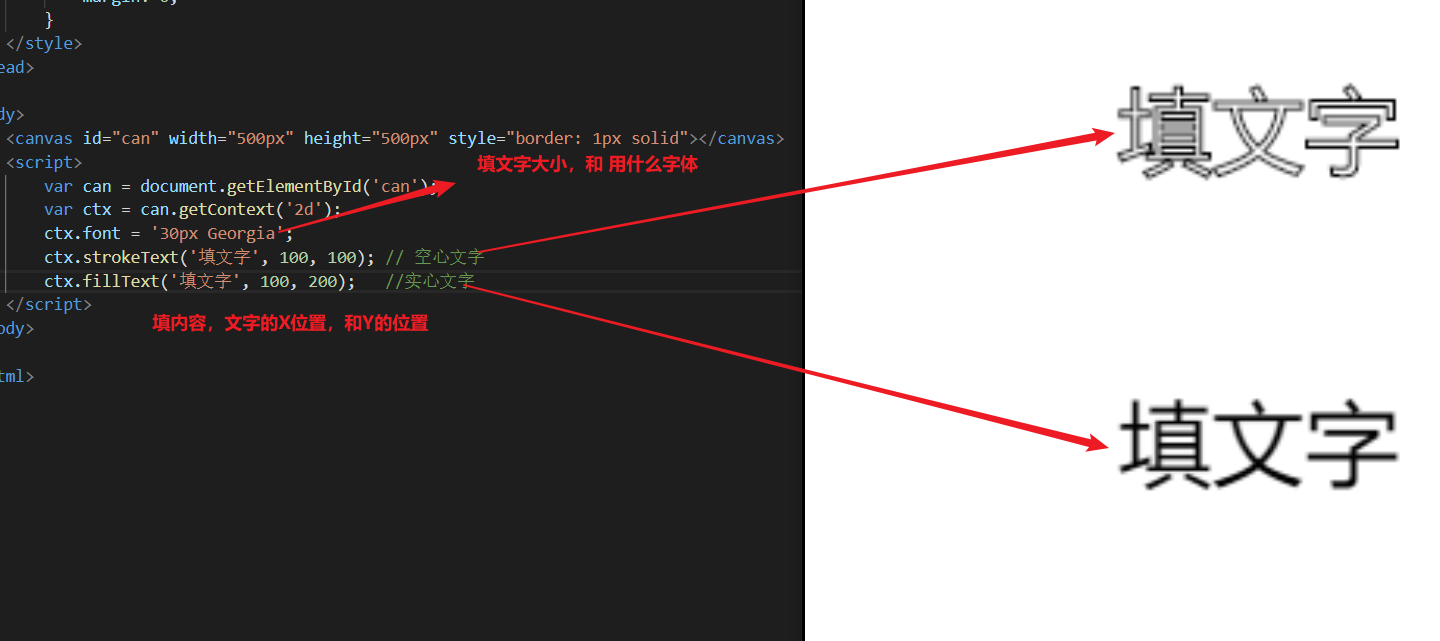
阴影效果

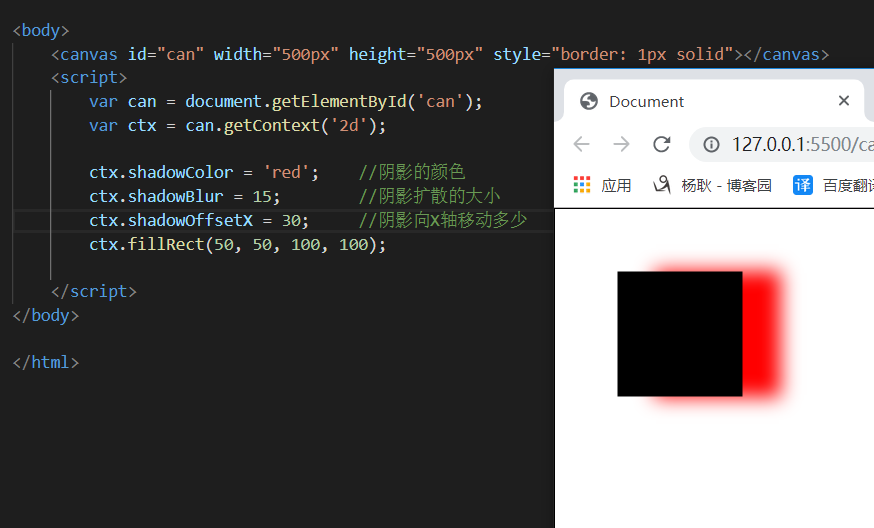
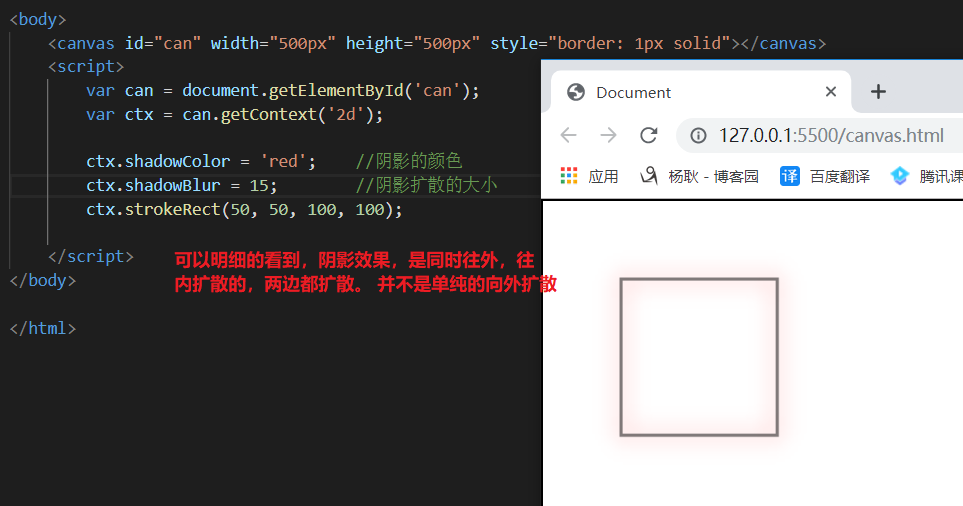
最后，补充：

改变线的粗细

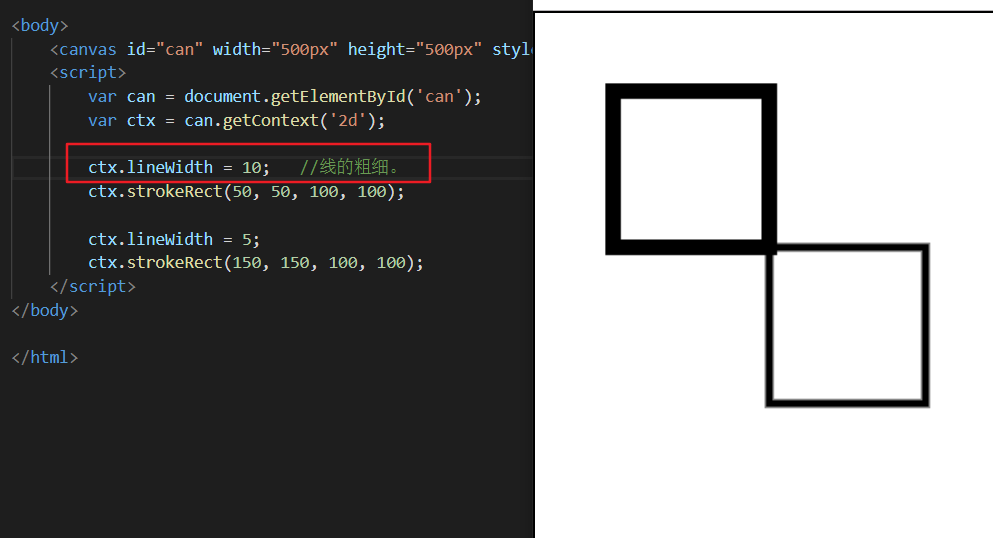
改变线的颜色

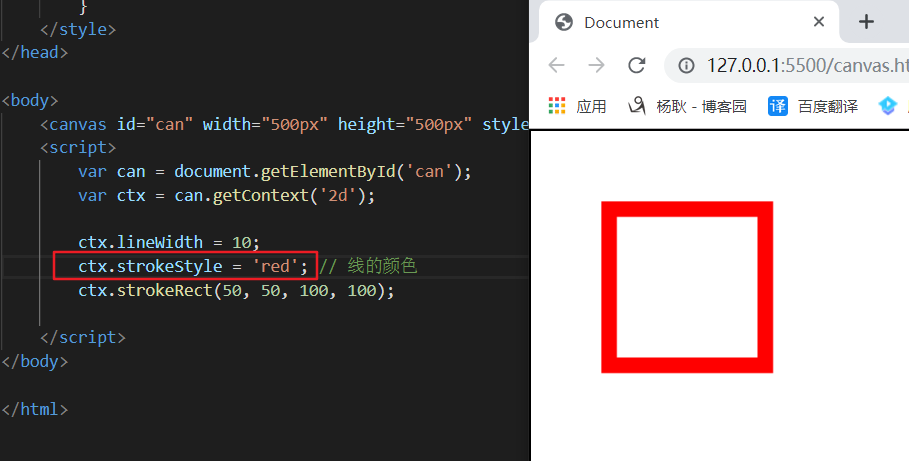
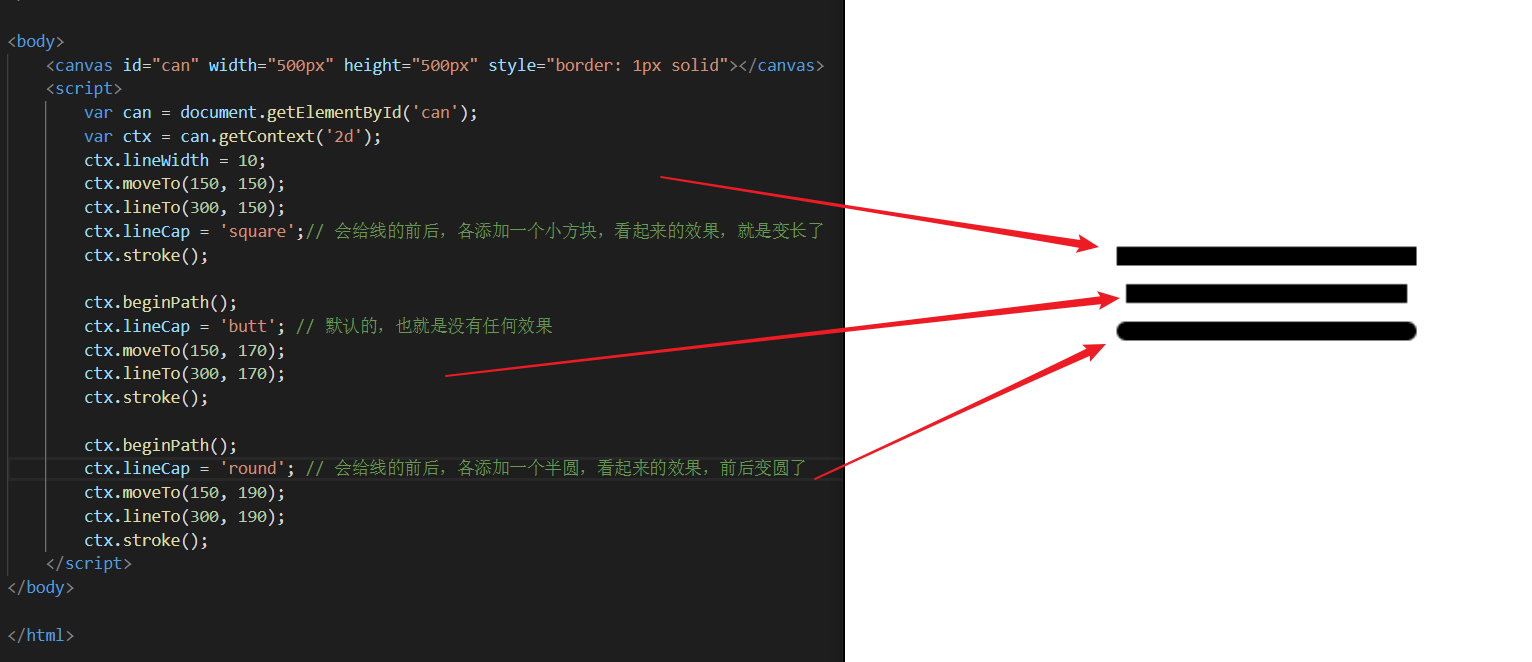
改变线起始与结尾的样式

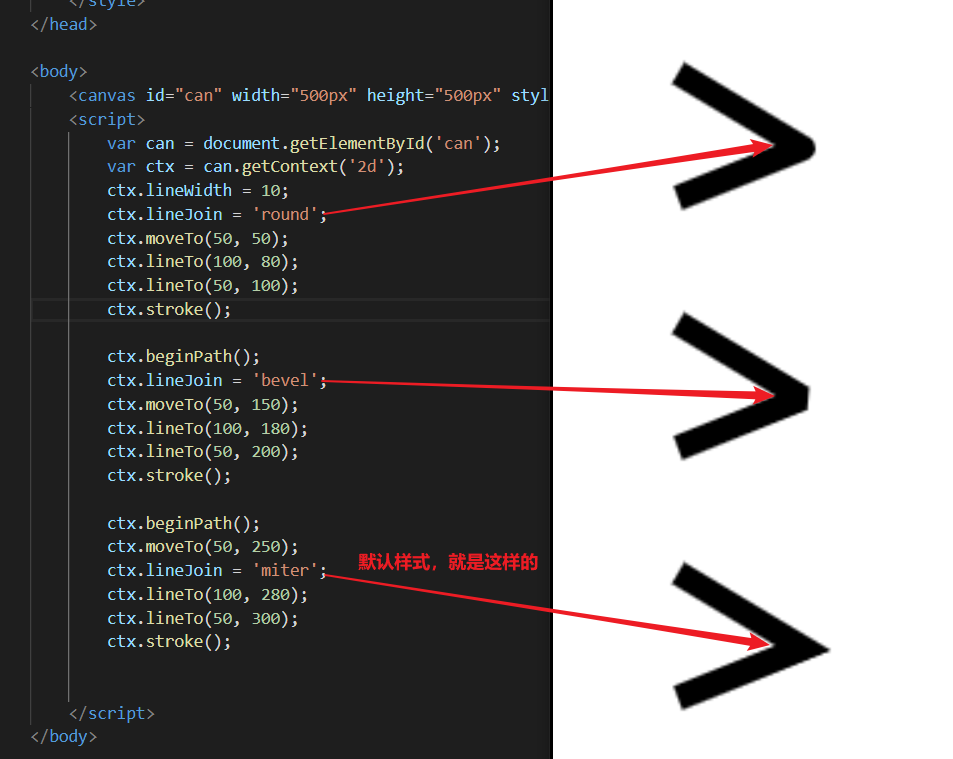
改变线于线之间的连接点样式

H5系列之canvas的更多相关文章

H5系列之History（必知必会）
H5系列之History(必知必会) 目录概念兼容性属性方法 H5方法概念理解History Api的使用方式目的是为了解决哪些问题作用:ajax获取数据时 ...
H5上传图片之canvas
H5上传图片之canvas,使用canvas处理压缩图片再上传 html代码: <form action="" method="post"> < ...
[Web Chart系列之六] canvas Chart 导出图文件
前言博主正在参加CSDN2013年度博客之星评选,如果这篇文章对您有用,请投他一票: 投票地址:http://vote.blog.csdn.net/blogstaritem/blogstar2013 ...
零元学Expression Blend 4 - Chapter 9 用实例了解布局容器系列-「Canvas」
原文:零元学Expression Blend 4 - Chapter 9 用实例了解布局容器系列-「Canvas」本系列将教大家以实做案例认识Blend 4 的布局容器,此章介绍的布局容器是Blen ...
用H5中的Canvas等技术制作海报
在去年的时候也实现过合成海报的功能,不过当时时间仓促,实现的比较简单. 就一个旋转功能,图片也不能拖动放大,也不能裁剪. 去年的实现可以参考<移动图片操作--上传>和<移动图片操作- ...
H5神器之canvas应用——网页修改保存图片
因为最近项目上的要求,需要在页面中可以对一张图片进行涂改和添加文字,然后再保存到(服务器)本地,因为也是第一次接触这方面的,然后爬网页啊爬网页,之后发现了一款adobe开发的一款插件,适合 Anroi ...
关于H5中的Canvas API的探索
Canvas API 是H5中比较炫酷的一部分内容.可以通过它动态的生成和展示图形.图表.图像以及动画.下面我将学习一下Canvas API. 最后有书籍和源码. 一.概述: 1.基本元素: 在网页上 ...
从web图片裁剪出发：了解H5中的canvas
本篇内容不针对canvas文档对每个api进行逐个的详解! 本篇内容不针对canvas文档对每个api进行逐个的详解! 本篇内容不针对canvas文档对每个api进行逐个的详解! 重说三,好了,现在进 ...
H5之画布canvas小记，以及通过画布实现原子无规则运动
我们知道html在h5出之前就仅仅只是一个标签,一个标记,语义化并不强,后来新增的标签如video,audio都是语义化更强(让人一看就懂是什么东西,反正我是这么理解的,一个div不代表着什么),本身 ...

随机推荐

Linux系列:快捷键、目录结构、用户目录
一.快捷键 1.历史命令查看历史命令:history [root@centos-master ~]# history 1 2020-10-25 21:03:39 2 2020-09-17 20:43 ...
攻防世界-mfw
打开题目,让我们看看about这个链接是什么,我们看到了这个他说他写这个站点用了git.php.bootstrap这很容易就能让我们想到,git源码泄露,这我们直接掏出githack, python ...
强网杯web之假的反序列化漏洞
说明打强网杯的时候一直在写论文, 做林逸师傅的培训题目. 现在得空,还是看了一部分的题目和wp. 源码源码一共三部分, 这里只写下我知识盲区的一部分,作为自己的记录. <?php highl ...
Retrofit学习
---恢复内容开始--- public class MainActivity extends AppCompatActivity { @Override protected void onCreate ...
(PatchGANs)Pecomputed Real-time Texture Synthesis With Markovian Generative Adversarial Networks
Introduction: Deconvolution; Computational costs; Strided convolutional nets; Markov patches; 1. Q ...
git 移除远程仓库关联
1 git remote rm origin // 移除本地关联 2 git remote add origin git@github.com/example.git // 添加线上仓库 3 git ...
Centos7中MySQL8.0安装过程及遇到的问题记录
本文主要参考以下2篇文章,安装操作 https://www.miboxapp.com/article/detail/1146659339214393344 https://blog.csdn.net/ ...
Python+Django实现微信扫码支付流程
Python+Django实现微信扫码支付流程关注公众号"轻松学编程"了解更多. 获取源码可以加我微信[1257309054],文末有二维码. [微信公众号支付官网]https: ...
Vue的生命周期--代码片段
Vue 实例有一个完整的生命周期,也就是从开始创建. 初始化数据. 编译模板. 挂载 Dom. 渲染→更新→渲染. 销毁等一系列过程,我们称这是 Vue 的生命周期.通俗说就是 Vue 实例从创建到销 ...
# Maven:Could not transfer artifact org.springframework:spring-webmvc:pom:。。。（系统找不到文件），从网上clone到本地的项目报红
解决办法: 确保maven配置正确,在maven的setting.xml配置文件中, 配置本地仓库路径 <localRepository>D:\Maven\文件名</localRep ...

H5系列之canvas

H5系列之canvas的更多相关文章

随机推荐

热门专题