[Fundamental of Power Electronics]-PART I-3.稳态等效电路建模，损耗和效率-3.2 考虑电感铜损

3.2 考虑电感铜损

可以拓展图3.3的直流变压器模型，来对变换器的其他属性进行建模。通过添加电阻可以模拟如功率损耗的非理想因素。在后面的章节，我们将通过在等效电路中添加电感和电容来模拟变换器动态。

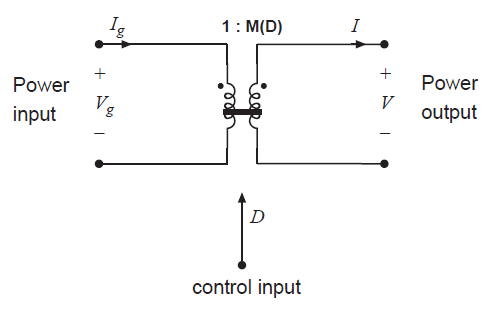
Fig 3.3 DC transformer

让我们来考虑下Boost电路中电感的铜损。实际电感器会表现出两种功率损耗：(1)由导线电阻导致的铜损；(2)由磁芯中的磁滞和涡流导致的磁芯损耗。图3.5给出了使用电感器与电阻\(R_{L}\)串联的结构描述了适合电感器铜损的模型。所以实际电感就是包含理想电感\(L\)串联铜损电阻\(R_L\)。

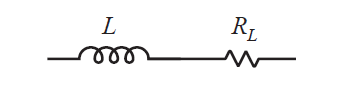
Fig 3.5 Modeling inductor copper loss via series resistor \(R_L\)

将图3.5的电感器模型插入到图3.6的Boost变换器中。现在可以使用电感的伏秒平衡，电容的电荷平衡和小纹波近似原理，以与理想无损变换器相同的方式分析电路。首先我们绘制两个子间隔内的变换器电路，如图3.7所示。

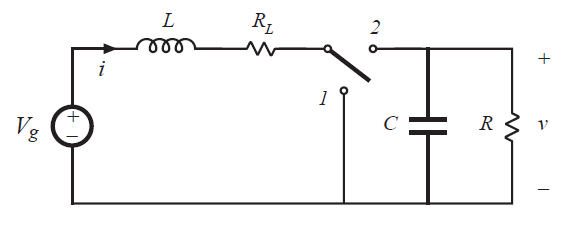
Fig 3.6 Insert this inductor model into boost converter circuit

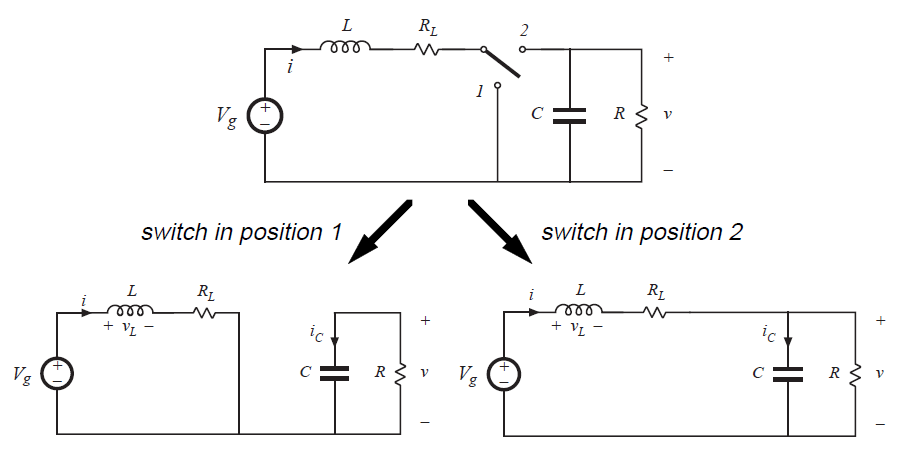
Fig 3.7 Analysis of nonideal boost converter

当\(0<t<D T_{s}\)，开关位于位置1，理想电感\(L\)两端的电感电压\(v_{L}(t)\)为

\[v_{L}(t)=V_{g}-i(t)R_{L} \tag{3.6}
\]

电容电流\(i_{C}(t)\)为：

\[i_{C}(t) = -\frac{v(t)}{R} \tag{3.7}
\]

然后，通过假定电感电流\(i(t)\)和电容电压\(v(t)\)的开关纹波相比其直流分量\(I\)和\(V\)非常小来简化上述方程。也就是，\(i(t) \approx I\)，\(v(t) \approx V\)，则方程(3.6)和(3.7)为：

\[v_{L}(t) = V_{g} - IR_{L} \\i_{C}(t) = -\frac{V}{R} \tag{3.8}
\]

当\(DT_{s}<t<T_{s}\)时，开关位于位置2，电感电流和电容电压表示为：

\[v_{L}(t)=V_{g}-i(t)R_{L} - v(t) \approx V_{g} -IR_{L}-V \\i_C(t) = i(t) - \frac{v(t)}{R} \approx I- \frac{V}{R} \tag{3.9}
\]

同样进行小纹波近似。

现在可以调用电感伏秒平衡原理。公式(3.8)和(3.9)可以用来构建图3.8中的电感电压波形。电感电压\(v(t)\)的直流分量或者说平均值为：

\[<v_{L}(t)>= \frac{1}{T_{s}} \int _{0} ^{T_{s}} v_{L}(t) dt =D(V_{g} - IR_{L})+D^{'}(V_{g}-IR_{L}-V) \tag{3.10}
\]

令\(<v_{L}>\)为0，化简可得：

\[0=V_{g} -IR_{L}-D^{'}V \tag{3.11}
\]

可以看出，电感器绕组电阻为电感伏秒平衡方程式增加了另一项。在第二章的理想Boost变换器(\(R_{L}=0\)),我们能够直接针对电压变换比(\(V/V_{g}\))求解该方程。而因为电感电流\(I\)是未知的，所以式(3.11)不能直接用这种方法求解。为了估计\(I\)，需要额外的方程。

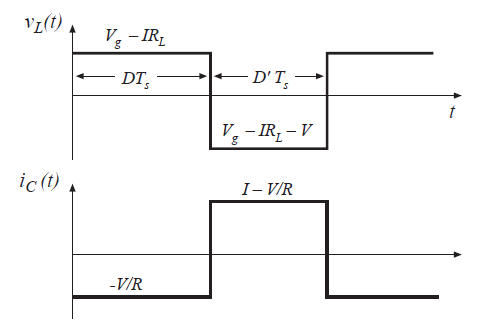
Fig 3.8 Inductor voltage and capacitor current waveforms，for the nonideal boost converter of Fig 3.6

额外方程就是使用电容电荷平衡得到的。电容电流\(i_{C}(t)\)波形如图3.8所示。电容电流的直流分量或者说平均值为：

\[<i_{C}(t)>=D( - \frac{V}{R}) + D^{'}(I- \frac{V}{R}) \tag{3.12}
\]

令\(<i_{C}>\)为零，整理后得到：

\[0 = D^{'}I- \frac{V}{R} \tag{3.13}
\]

现在我们有了(3.11)和(3.13)两个方程，\(V\)和\(I\)两个变量，消去\(I\)，求解\(V\)，可以得到：

\[\frac{V}{V_{g}} = \frac{1}{D^{'}} \frac{1}{1+ \frac{R_{L}}{D^{'2}R}} \tag{3.14}
\]

这就是变换器输出电压的求解方法。图3.9中绘制了在几个不同\({R_{L}}/{R}\)情况下的图形。可以从式(3.14)中看出，其包含两个部分，其一，\(1/D^{'}\)是当\(R_{L}=0\)时的理想变换比。其二，\(1/(1+R_{L}/D^{'2}R)\)，描绘了电感绕组电阻的影响。如果\(R_{L}\)远小于\(D^{'2}R\)，第二项即可认为其近似等于1，同时变换比近似等于理想值\(1/D^{'}\)。然而，随着\(R_{L}\)相对于\(D^{'2}R\)的增加，第二项的值减小，那么\(V/V_{g}\)也就减小了。

当占空比\(D\)接近1时，电感绕组\(R_L\)导致了\(V/V_{g}\)曲线有较大的变化。然后曲线趋近于0，而不是在\(D=1\)时接近无穷大。当然，期望变换器输出电压无穷大本身就是不合理的。工程师应该欣慰的是，现在的模型更加接近实际。\(D=1\)时发生的情况是，开关始终处于位置1，电感器从未连接到输出，因此没有能量传递到输出，并且输出电压趋近于0。由于仅受电感电阻\(R_{L}\)限制，电感电流趋于非常大的值。电感绕组中损耗了大量功率，\(V_{g}^2/R_{L}\)，同时没有功率传递到输出。因此我们可以预测，在\(D=1\)时，变换器效率趋近于0。

图3.9的另一个含义是电感绕组电阻限制了变换器能够输出的最大电压。例如：当\(R_{L}/R=0.02\)时，可以看到\(V/V_{g}\)的最大值接近3.5。如果期望获得\(V/V_{g}=5\)，那么根据图3.9，电感绕组电感必须减小到小于负载电阻\(R\)的1%。唯一的问题是，减小电感器的绕组电阻需要构建更大，更重，更昂贵的电感器。因此，通常重要的是通过正确建模如\(R_{L}\)的损耗元素的影响，并选择能够完成任务的最小的电感器来优化设计。现在我们有了能够执行这个操作所需的分析工具了。

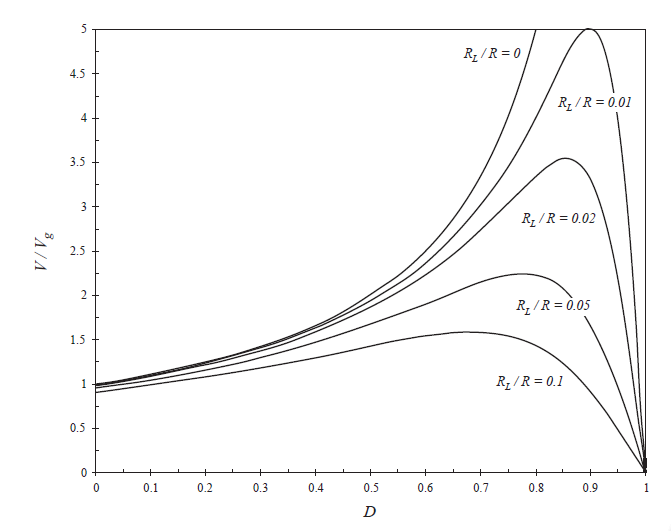
Fig 3.9 Solution for output voltage