洛谷 P3627 [APIO2009]抢掠计划 Tarjan缩点+Spfa求最长路

题目地址：https://www.luogu.com.cn/problem/P3627

第一次寒假训练的结测题，思路本身不难，但对于我这个码力蒟蒻来说实现难度不小…考试时肛了将近两个半小时才刚肛出来。我也是吐了

题面

Siruseri 城中的道路都是单向的。不同的道路由路口连接。按照法律的规定， 在每个路口都设立了一个 Siruseri 银行的 ATM 取款机。令人奇怪的是，Siruseri 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。

Banditji 计划实施 Siruseri 有史以来最惊天动地的 ATM 抢劫。他将从市中心 出发，沿着单向道路行驶，抢劫所有他途径的 ATM 机，最终他将在一个酒吧庆 祝他的胜利。

使用高超的黑客技术，他获知了每个 ATM 机中可以掠取的现金数额。他希 望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可 以经过同一路口或道路任意多次。但只要他抢劫过某个 ATM 机后，该 ATM 机 里面就不会再有钱了。 例如，假设该城中有 6 个路口，道路的连接情况如下图所示：



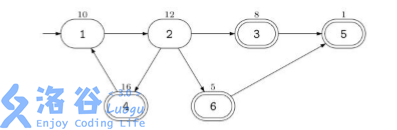
市中心在路口 1，由一个入口符号→来标识，那些有酒吧的路口用双圈来表

示。每个 ATM 机中可取的钱数标在了路口的上方。在这个例子中，Banditji 能抢 劫的现金总数为 47，实施的抢劫路线是：1-2-4-1-2-3-5。

输入格式

第一行包含两个整数 N、M。N 表示路口的个数，M 表示道路条数。接下来 M 行，每行两个整数，这两个整数都在 1 到 N 之间，第 i+1 行的两个整数表示第 i 条道路的起点和终点的路口编号。接下来 N 行，每行一个整数，按顺序表示每 个路口处的 ATM 机中的钱数。接下来一行包含两个整数 S、P，S 表示市中心的 编号，也就是出发的路口。P 表示酒吧数目。接下来的一行中有 P 个整数，表示 P 个有酒吧的路口的编号。

样例输入：

		6 7
		1 2
		2 3
		3 5
		2 4
		4 1
		2 6
		6 5
		10
		12
		8
		16
		1
		5
		1 4
		4 3 5 6

输出格式

输出一个整数，表示 Banditji 从市中心开始到某个酒吧结束所能抢劫的最多 的现金总数。

样例输出：47

思路：

由题给的图可以看出来，图中存在环，而每个边和点都可以重复走，那么我们可以从从环的任意一点起，无限制地到达环上的任意一点，所以我们可以把整个环看成一个点，环点的权是环上点权的和，这很容易联想到Tarjan缩点把原图化成DAG图；

然后题目让求最大的总权值，最常规的做法就是用Spfa跑最长路；

（有位很厉害的学长改装了Dijskra…，并坚信它能跑DAG的最长路，我们戏称为堆劣化Spfa…遗憾的是我并没有学会…)

这样，我们确定了大体的思路：Tarjan缩点+Spfa求最长路

代码的实现（重头戏来了）

emm…看看这堆数组就能明白这题有点恶心

所以我觉得分步来讲比较好

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=5*1e5+10;
int n,m,dis[maxn],money[maxn];
bool inq[maxn];
int from[maxn],to[maxn];
int head[maxn],dfn[maxn],low[maxn],dfs_clock=0;
int sta[maxn],scc_cnt=0,siz[maxn],top=0,belong[maxn],len=0,cnt[maxn];

1. 前置准备
   
   前向星存图，基本操作：

struct Edge{
    int from,to,next,dis;
}edge[maxn*2];
void Add(int a,int b,int c){
    edge[++len].to=b;
    edge[len].from=a;
    edge[len].next=head[a];
    edge[len].dis=c;
    head[a]=len;
}

1. Tarjan函数 这里我用的是数组模拟栈，即sta数组，top为栈顶； 其他的和普通的Tarjan模板没甚不一样

void Tarjan(int u){
    dfn[u]=low[u]=++dfs_clock;
    sta[++top]=u;//++top不要写成top++
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(!dfn[v]){
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(!belong[v]) low[u]=min(low[u],dfn[v]);
    }//这里省去了一个bool型vis数组，因为v如果入了栈，belong[v]的值
    //会被修改，不再是0，这就跟vis的效果一样
    if(dfn[u]==low[u]){
        int f=++scc_cnt;//scc_cnt记录强连通分量的个数
        while(true){
            int x=sta[top--];
            belong[x]=f;
            siz[f]+=money[x];//siz数组记录每个环的总权值
            if(x==u) break;
        }
    }
}

1. 主函数部分
   
   Spfa函数涉及到一些小细节，所以先上主函数再说Spfa

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
    	//这里最好是开两个数组把边记下来，一会建图会用到
        scanf("%d%d",&from[i],&to[i]);
        //懒人为了少写一个Add函数，直接用0当权值
        Add(from[i],to[i],0);
    }
    for(int i=1;i<=n;i++) scanf("%d",&money[i]);
    for(int i=1;i<=n;i++)//缩点，常规操作
        if(!dfn[i]) Tarjan(i);
    New();//建图函数，下步就说
    int U,P;scanf("%d%d",&U,&P);
    Spfa(U);//下下步说
    int ans=0;
    for(int i=1;i<=P;i++){
    	//遍历各个酒馆，找最远的那个就行
        int x;scanf("%d",&x);
        ans=max(ans,dis[belong[x]]);
    }
    printf("%d\n",ans);
    return 0;
}

1. New函数
   
   这个函数是建一个缩点后的新图让Spfa跑

void New(){
	//为节省空间直接清空原图就好，不用再新开
    memset(edge,0,sizeof(edge));
    memset(head,0,sizeof(head));
    len=0;
    for(int i=1;i<=m;i++){
    	//同环内的点无需存
        if(belong[from[i]]!=belong[to[i]]){
        	//这里我直接存了环的原权，如果愿意也可以存负权跑最短路
            Add(belong[from[i]],belong[to[i]],siz[belong[to[i]]]);
        }
    }
}

可能有人注意到我这里在存边权时只存了belong[to[i]]的权，也就是边指向的那个点所在的环的权，那from所在的环的权又该怎办呢

那么，这就是一会Spfa需要注意的细节了（其实就一行…）

1. Spfa函数（重重头戏来了）

大部分和Spfa的板子没区别，要点写在了注释里

queue<int> q;
void Spfa(int u){
    for(int i=1;i<=scc_cnt;i++){
        dis[i]=0;
        inq[i]=false;
        cnt[i]=0;
    }
    //这里就是全题最精髓也是最不容易注意的地方...
    //首先，我们并不确定起点u的位置，它可能是一个独立的点，也可能
    //属于一个环，所以，我们要把u直接当成环处理
    int U=belong[u];
    //再者，因为我们的边权只存了“去环”的权，那么原环的权就丢失了
    //所以这里dis的起点不再是0，而是起始点的环权，避免了权丢失
    dis[U]=siz[U];

    cnt[U]=1;
    inq[U]=1;
    q.push(U);
    while(!q.empty()){
        int uu=q.front();q.pop();
        inq[uu]=false;
        for(int i=head[uu];i;i=edge[i].next){
            int v=edge[i].to;
            //求最长路，所以是<，最短路则是>
            if(dis[v]<dis[uu]+edge[i].dis){
                dis[v]=dis[uu]+edge[i].dis;
                if(!inq[v]){
                    inq[v]=true;
                    q.push(v);
                }
            }
        }
    }
}//每次看到spfa后面这一长串括号就觉得心慌

这样，代码的各部分就完成了。纵观整道题，我们发现思路并不复杂，代码都是由基础的模板拼上的，我们所要重点考虑的是两者结合后会相互对对方产生怎样的影响，这里主要就是Tarjan缩点后对边权的影响

（考试的时候我为了找这个错找了两个小时…完蛋玩意儿）

最后

放上全部代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
const int maxn=5*1e5+50;
int n,m,dis[maxn],money[maxn];
bool inq[maxn];
int from[maxn],to[maxn];
int head[maxn],dfn[maxn],low[maxn],dfs_clock=0;
int sta[maxn],scc_cnt=0,siz[maxn],top=0,belong[maxn],len=0,cnt[maxn];
struct Edge{
    int from,to,next,dis;
}edge[maxn*2];
void Add(int a,int b,int c){
    edge[++len].to=b;
    edge[len].from=a;
    edge[len].next=head[a];
    edge[len].dis=c;
    head[a]=len;
}
void Tarjan(int u){
    dfn[u]=low[u]=++dfs_clock;
    sta[++top]=u;
    for(int i=head[u];i;i=edge[i].next){
        int v=edge[i].to;
        if(!dfn[v]){
            Tarjan(v);
            low[u]=min(low[u],low[v]);
        }
        else if(!belong[v]) low[u]=min(low[u],dfn[v]);
    }
    if(dfn[u]==low[u]){
        int f=++scc_cnt;
        while(true){
            int x=sta[top--];
            belong[x]=f;
            siz[f]+=money[x];
            if(x==u) break;
        }
    }
}
queue<int> q;
void Spfa(int u){
    for(int i=1;i<=scc_cnt;i++){
        dis[i]=0;
        inq[i]=false;
        cnt[i]=0;
    }
    int U=belong[u];
    cnt[U]=1;dis[U]=siz[U];inq[U]=1;
    q.push(U);
    while(!q.empty()){
        int uu=q.front();q.pop();
        inq[uu]=false;
        for(int i=head[uu];i;i=edge[i].next){
            int v=edge[i].to;
            if(dis[v]<dis[uu]+edge[i].dis){
                dis[v]=dis[uu]+edge[i].dis;
                if(!inq[v]){
                    inq[v]=true;
                    q.push(v);
                }
            }
        }
    }
}
void New(){
    memset(edge,0,sizeof(edge));
    memset(head,0,sizeof(head));
    len=0;
    for(int i=1;i<=m;i++){
        if(belong[from[i]]!=belong[to[i]]){
            Add(belong[from[i]],belong[to[i]],siz[belong[to[i]]]);
        }
    }
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++){
        scanf("%d%d",&from[i],&to[i]);
        Add(from[i],to[i],0);
    }
    for(int i=1;i<=n;i++) scanf("%d",&money[i]);
    for(int i=1;i<=n;i++)
        if(!dfn[i]) Tarjan(i);
    New();
    int U,P;scanf("%d%d",&U,&P);
    Spfa(U);
    int ans=0;
    for(int i=1;i<=P;i++){
        int x;scanf("%d",&x);
        ans=max(ans,dis[belong[x]]);
    }
    printf("%d\n",ans);
    return 0;
}

小小萌新第一次写博客，感觉还是比较认真的

如果有大佬看见什么不对的地方还请在法律允许的范围内嘲笑我orz

溜了溜了