【转转】 Huber Loss

原文地址：

https://www.cnblogs.com/nowgood/p/Huber-Loss.html

======================================================

Huber Loss 是一个用于回归问题的带参损失函数, 优点是能增强平方误差损失函数(MSE, mean square error)对离群点的鲁棒性。

当预测偏差小于 δ 时，它采用平方误差,

当预测偏差大于 δ 时，采用的线性误差。

相比于最小二乘的线性回归，HuberLoss降低了对离群点的惩罚程度，所以 HuberLoss 是一种常用的鲁棒的回归损失函数。

Huber Loss 定义如下

Lδ(a)={12a2,δ⋅(|a|−12δ),for |a|≤δ,otherwise.



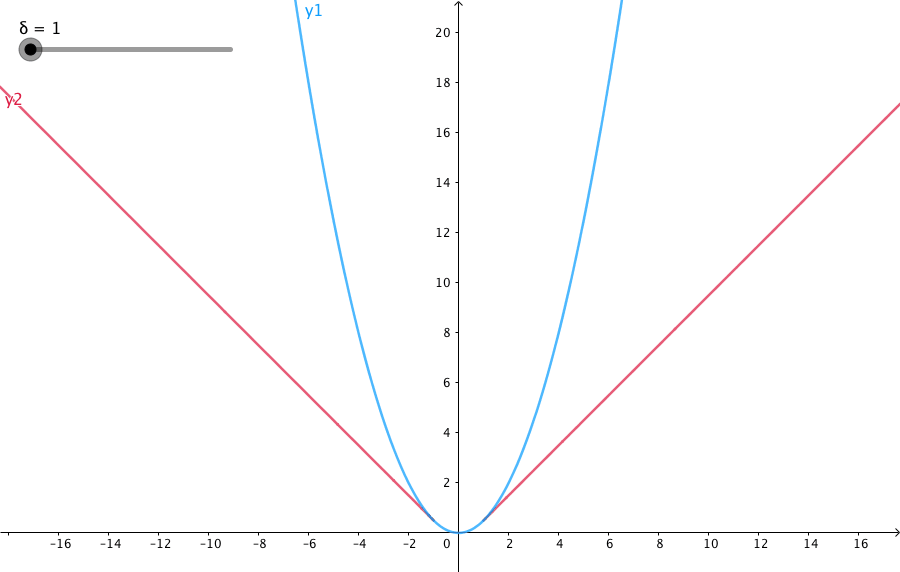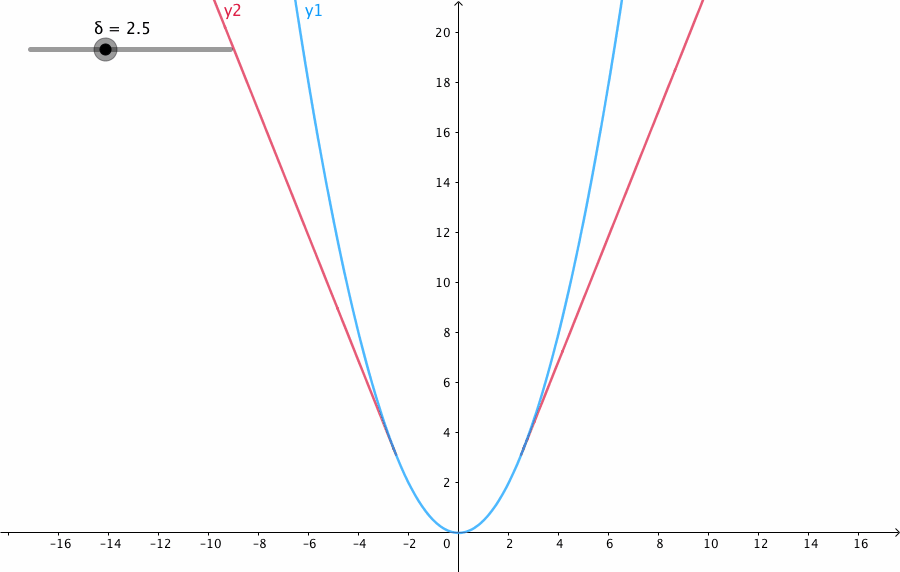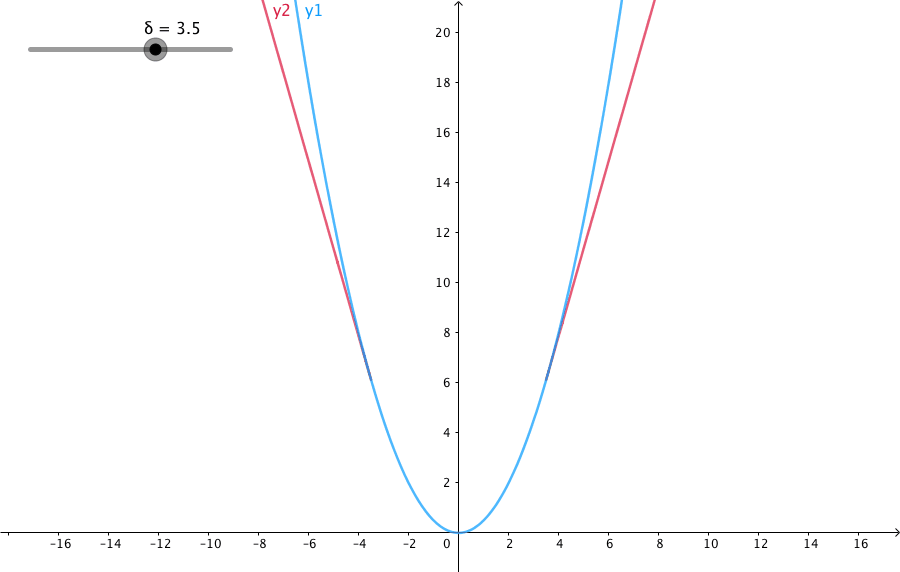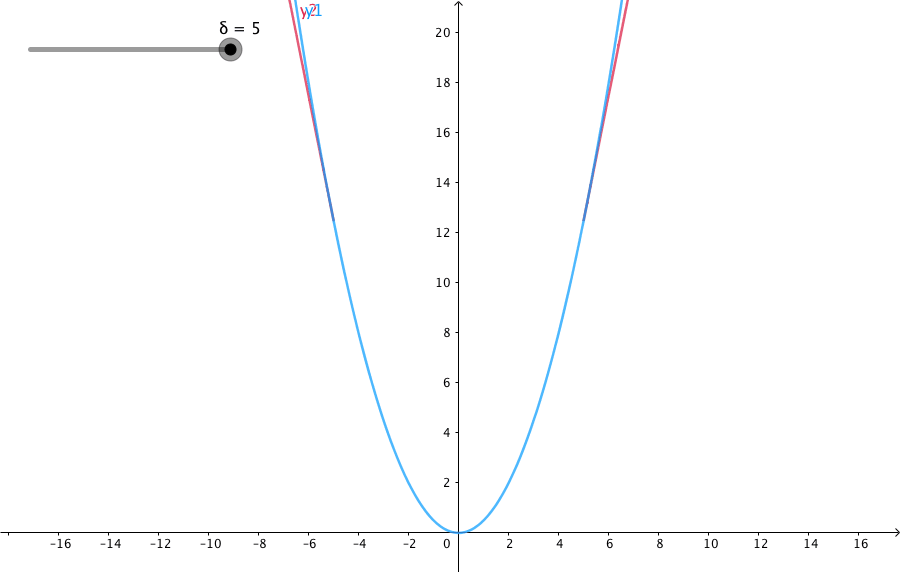
参数 a 通常表示 residuals，写作 y−f(x)，当 a = y−f(x) 时，Huber loss 定义为：

Lδ(y,f(x))={12(y−f(x))2,δ⋅(|y−f(x)|−12δ),for |y−f(x)|≤δotherwise.

δ 是 HuberLoss 的参数，y是真实值，f(x)是模型的预测值, 且由定义可知 Huber Loss 处处可导