Luogu P2831 愤怒的小鸟(状压+记忆化搜索)

P2831 愤怒的小鸟

题意

题目描述

Kiana最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于$(0,0)$处，每次Kiana可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如$y=ax^2+bx$的曲线，其中$a,b$是Kiana指定的参数，且必须满足$a<0$，$a,b$都是实数。

当小鸟落回地面（即$x$轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有$n$只绿色的小猪，其中第$i$只小猪所在的坐标为$\left(x_i,y_i \right)$。

如果某只小鸟的飞行轨迹经过了$\left( x_i, y_i \right)$，那么第$i$只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过$\left( x_i, y_i \right)$，那么这只小鸟飞行的全过程就不会对第$i$只小猪产生任何影响。

例如，若两只小猪分别位于$(1,3)\(和\)(3,3)$，Kiana可以选择发射一只飞行轨迹为$y=-x^2+4x$的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有$T$个关卡，现在Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数$T$，表示游戏的关卡总数。

下面依次输入这$T$个关卡的信息。每个关卡第一行包含两个非负整数$n,m$，分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的$n$行中，第$i$行包含两个正实数$x_i,y_i$，表示第$i$只小猪坐标为$(x_i,y_i)$。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果$m=0$，表示Kiana输入了一个没有任何作用的指令。

如果$m=1$，则这个关卡将会满足：至多用$\lceil n/3 + 1 \rceil$只小鸟即可消灭所有小猪。

如果$m=2$，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少$\lfloor n/3 \rfloor$只小猪。

保证$1\leq n \leq 18$，$0\leq m \leq 2$，$0<x_i,y_i<10$，输入中的实数均保留到小数点后两位。

上文中，符号$\lceil c \rceil$和$\lfloor c \rfloor$分别表示对$c$向上取整和向下取整，例如$\lceil 2.1 \rceil = \lceil 2.9 \rceil = \lceil 3.0 \rceil = \lfloor 3.0 \rfloor = \lfloor 3.1 \rfloor = \lfloor 3.9 \rfloor = 3$。

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例

输入样例#1：

2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

输出样例#1：

1
1

输入样例#2：

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

输出样例#2：

2
2
3

输入样例#3：

1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99

输出样例#3：

6

说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，$2$只小猪分别位于$(1.00,3.00)\(和\)(3.00,3.00)$，只需发射一只飞行轨迹为$y=-x^2+4$的小鸟即可消灭它们。

第二个关卡中有$5$只小猪，但经过观察我们可以发现它们的坐标都在抛物线$y=-x^2+6$上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

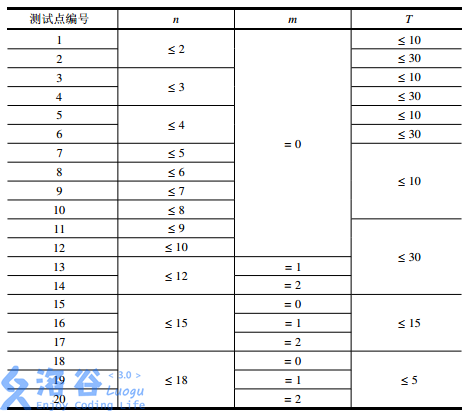
思路

我把去年的题做了下，感觉还好，动态规划不太会，而且这题好难。 --金总 2017.11.11

首先解决一个问题：对于二次函数$y=ax^2+bx$，因为其中有两个系数，所以两个点就可以确定这个函数中$a,b$的值：

\(ax_i^2+bx_i=y_i\)
\(ax_j^2+bx_j=y_j\)

相互消元得：

\(a=\frac{x_jy_i-x_iy_j}{x_ix_j(x_i-x_j)}\)
\(b=\frac{x_i^2y_j-x_j^2y_i}{x_ix_j(x_i-x_j)}\)

贪心地想，我们要想用最少的鸟去击杀所有的猪，那么每只鸟击杀的猪要尽量多。我们枚举每只鸟击杀的猪的其中两头，就可以得到其发射线路的二次函数，从而算出还有哪些猪也在该条函数上。

当然，有两个特例：

1. 若当前只剩下一只猪，那么这头猪必须用一只鸟来打，不能也不需要计算出鸟发射的二次函数。
2. 若当前的剩下的所有猪都无法“一鸟二猪”，那么我们就用一只鸟打一只猪。

哪些情况下所有的猪都无法“一鸟二猪”呢？首先，题目要求$a>0$，那么如果我们算出来$a<0$也就是二次函数开口向下，那么这样的函数是不可行的；其次，在上面的的方程中，分母部分有$x_i-x_j$，而且显然横坐标相同的两点不可能出现在同一条二次函数上（通过函数的定义），所以当$x_i=x_j$时，不可行。若所有的情况都归于不可行的情况时，当前就无法“一鸟二猪”了。

当然，这样的搜索时拿不了满分的，我们考虑加上这三条来优化其时间：

1. 对于当前场上存活的猪的状况，我们用一个二进制数$state$来表示。$state$上的第$k$位若为$0$，表示第$k$只猪未被击杀；若为$1$，表示第$k$只猪已被击杀，我们接下来的搜索中只击杀未击杀的猪。
2. 记忆化一：记录数组$bin[i][j]$记录击杀了$i,j$两只猪的同时可以击杀的猪。同样的，我们用一个二进制数来记录：$bin[i][j]$上的第$k$位若为$0$，表示第$k$只猪不可被击杀；若为$1$，表示第$k$只猪可被击杀。
3. 记忆化二：对于每一个$state$我们可能会多次搜索到。为了排除冗余搜索，我们记录$remember[state]$表示在$state$状态下再发射$remember[state]$只鸟就可以击杀所有的猪，我们就可以边搜索边记录，然后统计$remember$的值。

对于记忆化一，我们可以这么写：

void calc(double a,double b)//已经通过上面公式算出来的a和b
{
    vector<int>V;//开一个vector储存可以击杀的猪
    int state=0;//记录bin
    for(int i=0;i<n;i++)
        if(fabs(a*x[i]*x[i]+b*x[i]-y[i])<=0.000001)//注意精度判断
        {
            state|=(1<<i);//或运算在二进制上填1
            V.push_back(i);//放入vector中
        }
    for(int i=0;i<V.size();i++)
        for(int j=i+1;j<V.size();j++)
            bin[V[i]][V[j]]=bin[V[j]][V[i]]=state;//修改bin值
}

而主要的dfs过程就是这样的：

int dfs(int state)//当前壮态为state
{
    if(remember[state]!=-1) return remember[state];//已经搜索过了，直接返回
    remember[state]=0x3f3f3f3f;//记录remember状态
    for(int i=0;i<n;i++)
    {
        if(state&(1<<i)) continue;//这只猪已经死了
        bool flag=false;//判断有没有猪可以和它一起被杀掉
        for(int j=0;j<n;j++)
            if((state&(1<<j))==0&&x[i]!=x[j]&&(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]))<0.0)//判断是否可行
            {
                flag=true;//有猪可以和它一起被杀
                if(bin[i][j]==-1) calc((x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j])),(x[i]*x[i]*y[j]-x[j]*x[j]*y[i])/(x[i]*x[j]*(x[i]-x[j])));//运用上面的方程（说实话有点丑）
                remember[state]=min(remember[state],dfs(state|bin[i][j])+1);//更新remember为最优解
            }
        if(!flag) return remember[state]=dfs(state|(1<<i))+1;//这只猪只能自己被杀，所以remember[state]=remember[state|(1<<i)]+1，直接更新
    }
    return remember[state];//搜索结束，溜了溜了
}

这样就能$AC$辣。

AC代码

#include<bits/stdc++.h>
using namespace std;
int T,n,m,ans,bin[20][20],remember[1<<18];
double x[20],y[20];
void init()
{
    cin>>n>>m;
    ans=INT_MAX;
    for(int i=0;i<n;i++) cin>>x[i]>>y[i];
    memset(bin,-1,sizeof bin);
    memset(remember,-1,sizeof remember);
    remember[(1<<n)-1]=0;
}
void calc(double a,double b)
{
    vector<int>V;
    int state=0;
    for(int i=0;i<n;i++)
        if(fabs(a*x[i]*x[i]+b*x[i]-y[i])<=0.000001)
        {
            state|=(1<<i);
            V.push_back(i);
        }
    for(int i=0;i<V.size();i++)
        for(int j=i+1;j<V.size();j++)
            bin[V[i]][V[j]]=bin[V[j]][V[i]]=state;
}
int dfs(int state)
{
    if(remember[state]!=-1) return remember[state];
    remember[state]=0x3f3f3f3f;
    for(int i=0;i<n;i++)
    {
        if(state&(1<<i)) continue;
        bool flag=false;
        for(int j=0;j<n;j++)
            if((state&(1<<j))==0&&x[i]!=x[j]&&(x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j]))<0.0)
            {
                flag=true;
                if(bin[i][j]==-1) calc((x[j]*y[i]-x[i]*y[j])/(x[i]*x[j]*(x[i]-x[j])),(x[i]*x[i]*y[j]-x[j]*x[j]*y[i])/(x[i]*x[j]*(x[i]-x[j])));
                remember[state]=min(remember[state],dfs(state|bin[i][j])+1);
            }
        if(!flag) return remember[state]=dfs(state|(1<<i))+1;
    }
    return remember[state];
}
int main()
{
    cin>>T;
    while(T--)
    {
        init();
        printf("%d\n",dfs(0));
    }
    return 0;
}