matlab初探寻

 matlab
 <iframe src="//player.bilibili.com/player.html?aid=74994893&cid=128293306&page=1" scrolling="no" border="0" frameborder="no" framespacing="0" allowfullscreen="true"> </iframe>
 %使用要点：

 %.目标函数f要写成列矩阵的形式
 %.约束要写成<=的形式
 %.函数是为求最小值设置的
 %[x,fv,exitflag,output,lambda]=linprog(f,a,b,aeq,beq,lb,ub)
 %x表示最优解，以列矩阵表示
 %fval为最优值
 %exitflg=1有最优解，0迭代次数超过设定次数，-2约束区域不可行，-3问题无解，-4执行迭代算法时遇到NaN,
 %-5原问题和对偶问题均不可行，-7搜索方向太小，不能继续前进，output表明算法和迭代情况，lambda指的是存储情况。
 %输入部分如有缺失，可用[]代替
 %min z=-3x1-4x2
 %s.t x1+x2<=
 % x1+2x2<=
 % x2<=
 % x1,x2>=

 f=[-,-]';
 a=[1,1;1,2;0,1];
 b=[6,8,3]';
 lb=[,]';
 [x,fv,ex,output,lambda]=linprog(f,a,b,[],[],lb,[]);

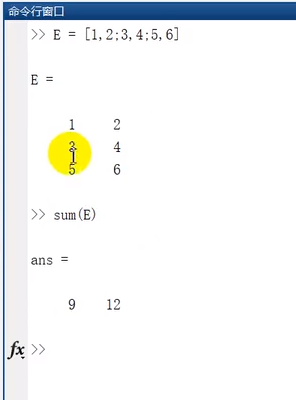
matlab根据列来排序的，先计算列在计算行

 可以通过 输入命令来球和，，，SUM( E,2)这个就是根据行来求和了

 a = sum(sum(E))先对列求和，再对行求和就饿可以做到全部求和了；太他妈极致了

A([2,5] , :)  %这个就是去到了所有的第二行和第五行的元素

A（2:5,:)     %这个就是说的取第二行到第五行的元素全部，2:5意思就是一个递增的数列；

2:1:5 这个就是以1为公差的等差数列

>> A =[,,,,;
,,,,;
,,,,];
>> sum_a = sum(A)

sum_a =

>> sum_a = repmat(sum_q,,)
未定义函数或变量 'sum_q'。

是不是想输入:
>> sum_a = repmat(sum_a,,)

sum_a =