第二十五篇玩转数据结构——链表（Linked List）

1.. 链表的重要性

我们之前实现的动态数组、栈、队列，底层都是依托静态数组，靠resize来解决固定容量的问题，而"链表"则是一种真正的动态数据结构，不需要处理固定容量的问题；
链表是最简单的动态数据结构；
学习链表有助于更深入的理解"引用"（或指针）；
学习链表有助于更深入的理解"递归"；
链表可以用来辅助组成其他数据结构；

2.. 链表基础

数据存储在"节点"（Node）中；
链表的形象化解释如下图：
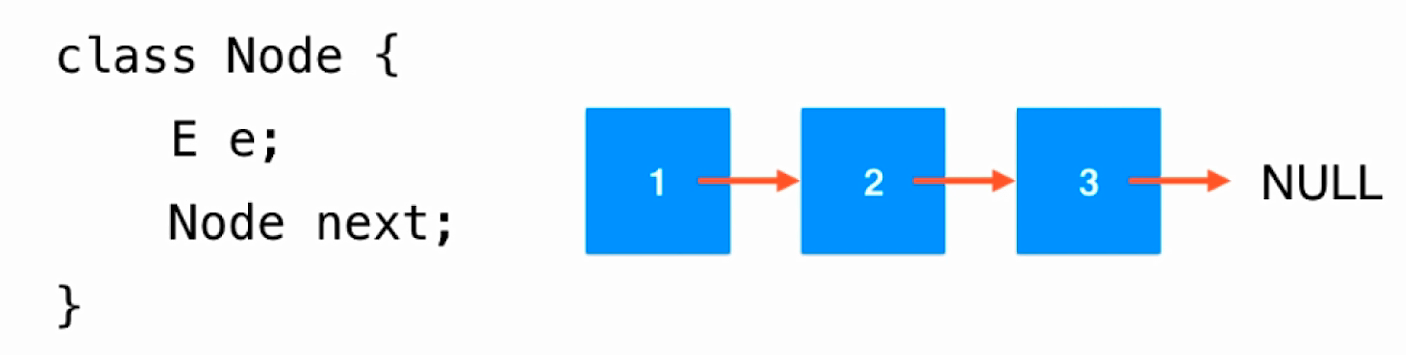
链表的优点在于，它是一种真正的动态数据结构，不需要处理固定容量问题；
链表的缺点在于，相较于数组，失去了随机访问的能力；
数组和链表的对比如下图所示：

3.. 链表的实现

实现链表的业务逻辑如下：

public class LinkedList<E> {

    private class Node {

        public E e;

        public Node next;

        //构造函数

        public Node(E e, Node next) {

            this.e = e;

            this.next = next;

        }

        //只传了参数e的构造函数

        public Node(E e) {

            this(e, null);

        }

        //不传递参数的构造函数

        public Node() {

            this(null, null);

        }

        //方便打印测试

        @Override

        public String toString() {

            return e.toString();

        }

    }

    private Node dummyHead;

    private int size;

    //构造函数

    public LinkedList() {

        dummyHead = new Node(null, null);  //虚拟头节点

        size = 0;

    }

    //获取链表中的元素个数

    public int getSize() {

        return size;

    }

    //判断链表是否为空

    public boolean isEmpty() {

        return size == 0;

    }

    //在链表的index(0-based)位置添加新的元素e

    //在链表中不是一个常用操作

    public void add(int index, E e) {

        if (index < 0 || index > size) {

            throw new IllegalArgumentException("Add failed. Illegal index.");

        }

        Node prev = dummyHead;

        for (int i = 0; i < index; i++) {

            prev = prev.next;

        }

        prev.next = new Node(e, prev.next);

        size++;

    }

    //在链表头添加新元素e

    public void addFirst(E e) {

        add(0, e);

    }

    //在链表末尾添加新的元素e

    public void addLast(E e) {

        add(size, e);

    }

    //获取链表的index(0-based)位置的元素

    //在链表中也不是一个常用操作

    public E get(int index) {

        if (index < 0 || index > size - 1) {

            throw new IllegalArgumentException("Get failed. Illegal index.");

        }

        Node cur = dummyHead.next;

        for (int i = 0; i < index; i++) {

            cur = cur.next;

        }

        return cur.e;

    }

    //获得链表的第一个元素

    public E getFirst() {

        return get(0);

    }

    //获得链表的最后一个元素

    public E getLast() {

        return get(size - 1);

    }

    //修改链表的index(0-based)位置的元素为e

    //在链表中也不是一个常用操作

    public void set(int index, E e) {

        if (index < 0 || index > size - 1) {

            throw new IllegalArgumentException("Set failed. Illegal index.");

        }

        Node cur = dummyHead.next;

        for (int i = 0; i < index; i++) {

            cur = cur.next;

        }

        cur.e = e;

    }

    //查找链表中是否存在元素e

    public boolean contains(E e) {

        Node cur = dummyHead.next;

        while (cur != null) {

            if (cur.e.equals(e)) {

                return true;

            }

            cur = cur.next;

        }

        return false;

    }

    //删除链表的index(0-based)位置的元素，并返回该元素

    //在链表中也不是一个常用操作

    public E remove(int index) {

        if (index < 0 || index > size - 1) {

            throw new IllegalArgumentException("Remove failed. Illegal index.");

        }

        Node prev = dummyHead;

        for (int i = 0; i < index; i++) {

            prev = prev.next;

        }

        Node retNode = prev.next;

        prev.next = retNode.next;

        retNode.next = null;

        size--;

        return retNode.e;

    }

    //删除链表中的第一个元素，并返回该元素

    public E removeFirst() {

        return remove(0);

    }

    //删除链表中的最后一个元素，并返回该元素

    public E removeLast() {

        return remove(size - 1);

    }

    // 从链表中删除元素e

    public void removeElement(E e){

        Node prev = dummyHead;

        while(prev.next != null){

            if(prev.next.e.equals(e))

                break;

            prev = prev.next;

        }

        if(prev.next != null){

            Node delNode = prev.next;

            prev.next = delNode.next;

            delNode.next = null;

            size --;

        }

    }

    //方便打印测试

    @Override

    public String toString() {

        StringBuilder res = new StringBuilder();

//        Node cur = dummyHead.next;

//        while (cur != null) {

//            res.append(cur + "->");

//            cur = cur.next;

//        }

        for (Node cur = dummyHead.next; cur != null; cur = cur.next) {

            res.append(cur + "->");

        }

        res.append("NULL");

        return res.toString();

    }

}

测试的业务逻辑如下：

public class Main {

    public static void main(String[] args) {

        LinkedList<Integer> linkedList = new LinkedList<>();

        for (int i = 0; i < 5; i++) {

            linkedList.addFirst(i);

            System.out.println(linkedList);

        }

        linkedList.add(2, 666);

        System.out.println(linkedList);

        linkedList.remove(2);

        System.out.println(linkedList);

        linkedList.removeFirst();

        System.out.println(linkedList);

        linkedList.removeLast();

        System.out.println(linkedList);

    }

}

输出结果：

0->NULL

1->0->NULL

2->1->0->NULL

3->2->1->0->NULL

4->3->2->1->0->NULL

4->3->666->2->1->0->NULL

4->3->2->1->0->NULL

3->2->1->0->NULL

3->2->1->NULL

4.. 链表的时间复杂度分析：

添加操作 O(n)

addLast(e)     O(n)

addFirst(e)    O(1)

add(index, e)  O(n/2)=O(n)

删除操作 O(n)

removeLase(e)     O(n)

removeFirst(e)    O(1)

remove(index, e)  O(n/2)=O(n)

修改操作 O(n)
```
set(index, e)  O(n)
```
查找操作 O(n)
```
get(index)   O(n)

contains(e)  O(n)
```
总体来说，链表的增、删、改、查的时间复杂度都是O(n)
如果我们只对链表的头进行添加和删除操作，那么时间复杂度是O(1)，如果我们只查链表头的元素，那么时间复杂度也是O(1)，满足这些条件的数据结构，我们很容易就会想到"栈"，对于"栈"而言，遵循后进先出的原则，只对栈的一端，也就是"栈顶"进行操作，无论是添加、删除还是查看元素，都在栈顶进行。所以，我们就可以把链表头当作栈顶，用链表来作为栈的底层实现，来实现出一个栈。

5.. 使用链表来实现一个"栈"

链表栈的实现及测试的业务逻辑如下：

public class LinkedListStack<E> implements Stack<E> {

    private LinkedList<E> list;

    //构造函数

    public LinkedListStack() {

        list = new LinkedList<>();

    }

    //实现getSize方法

    @Override

    public int getSize() {

        return list.getSize();

    }

    //实现isEmpty方法

    @Override

    public boolean isEmpty() {

        return list.isEmpty();

    }

    //实现push方法

    @Override

    public void push(E e) {

        list.addFirst(e);

    }

    //实现pop方法

    @Override

    public E pop() {

        return list.removeFirst();

    }

    //实现peek方法

    @Override

    public E peek() {

        return list.getFirst();

    }

    //方便打印测试

    @Override

    public String toString() {

        StringBuilder res = new StringBuilder();

        res.append("Stack: top ");

        res.append(list);

        return res.toString();

    }

    //测试

    public static void main(String[] args) {

        LinkedListStack<Integer> stack = new LinkedListStack<>();

        //测试入栈push

        for (int i = 0; i < 5; i++) {

            stack.push(i);

            System.out.println(stack);

        }

        //测试出栈

        stack.pop();

        System.out.println(stack);

    }

}

输出结果：

Stack: top 0->NULL

Stack: top 1->0->NULL

Stack: top 2->1->0->NULL

Stack: top 3->2->1->0->NULL

Stack: top 4->3->2->1->0->NULL

Stack: top 3->2->1->0->NULL

6.. 数组栈与链表栈的性能比较

测试的业务逻辑如下：

import java.util.Random;

public class Main {

    //测试使用stack运行opCount个push和pop操作所需的时间，单位：秒

    private static double testStack(Stack<Integer> stack, int opCount) {

        long startTime = System.nanoTime();

        Random random = new Random();

        for (int i = 0; i < opCount; i++) {

            stack.push(random.nextInt(Integer.MAX_VALUE));

        }

        for (int i = 0; i < opCount; i++) {

            stack.pop();

        }

        long endTime = System.nanoTime();

        return (endTime - startTime) / 1000000000.0;

    }

    public static void main(String[] args){

        int opCount = 10000;

        ArrayStack<Integer> arrayStack = new ArrayStack<>();

        double time1 = testStack(arrayStack,opCount);

        System.out.println("ArrayStack, time: " + time1 + " s");

        LinkedListStack<Integer> linkedListStack = new LinkedListStack<>();

        double time2 = testStack(linkedListStack,opCount);

        System.out.println("LinkedListStack, time: " + time2 + " s");

        // 这二者的时间比较很复杂，ArrayStack会在扩容和缩容操作上面耗费时间，LinkedListStack则会在创建新的Node上面耗费时间

    }

}

这两种栈的时间复杂度基本处于相同的水平

7.. 使用链表实现一个"队列"

链表队列的实现及测试的业务逻辑如下

public class LinkListQueue<E> implements Queue<E> {

    private class Node {

        public E e;

        public Node next;

        public Node(E e, Node next) {

            this.e = e;

            this.next = next;

        }

        public Node(E e) {

            this(e, null);

        }

        public Node() {

            this(null, null);

        }

        @Override

        public String toString() {

            return e.toString();

        }

    }

    private Node head, tail;

    private int size;

    public LinkListQueue() {

        head = null;

        tail = null;

        size = 0;

    }

    //实现getSize

    @Override

    public int getSize() {

        return size;

    }

    //实现isEmpty

    @Override

    public boolean isEmpty() {

        return size == 0;

    }

    //实现enqueue

    @Override

    public void enqueue(E e) {

        if (tail == null) {

            tail = new Node(e);

            head = tail;

        } else {

            tail.next = new Node(e);

            tail = tail.next;

        }

        size++;

    }

    //实现dequeue

    @Override

    public E dequeue() {

        if (isEmpty()) {

            throw new IllegalArgumentException("Cannot dequeue from an empty queue.");

        }

        Node retNode = head;

        head = head.next;

        retNode.next = null;

        if (head == null) {

            tail = null;

        }

        size--;

        return retNode.e;

    }

    //实现getFront

    public E getFront() {

        if (isEmpty()) {

            throw new IllegalArgumentException("Queue is empty.");

        }

        return head.e;

    }

    //方便打印测试

    public String toString() {

        StringBuilder res = new StringBuilder();

        res.append("Queue: front ");

        Node cur = head;

        while (cur != null) {

            res.append(cur + "->");

            cur = cur.next;

        }

        res.append("NULL");

        return res.toString();

    }

    //测试

    public static void main(String[] args) {

        LinkListQueue<Integer> queue = new LinkListQueue<>();

        for (int i = 0; i < 6; i++) {

            queue.enqueue(i);

            System.out.println(queue);

            if (i % 3 == 2) {

                queue.dequeue();

                System.out.println(queue);

            }

        }

    }

}

输出结果：

Queue: front 0->NULL

Queue: front 0->1->NULL

Queue: front 0->1->2->NULL

Queue: front 1->2->NULL

Queue: front 1->2->3->NULL

Queue: front 1->2->3->4->NULL

Queue: front 1->2->3->4->5->NULL

Queue: front 2->3->4->5->NULL

8.. 数组队列、循环队列和链表队列的性能比较

测试的业务逻辑如下：

import java.util.Random;

public class Main {

    // 测试使用q运行opCount个enqueue和dequeue操作所需要的时间，单位：秒

    private static double testQueue(Queue<Integer> q, int opCount) {

        long startTime = System.nanoTime();

        Random random = new Random();

        for (int i = 0; i < opCount; i++) {

            q.enqueue(random.nextInt(Integer.MAX_VALUE));

        }

        for (int i = 0; i < opCount; i++) {

            q.dequeue();

        }

        long endTime = System.nanoTime();

        return (endTime - startTime) / 1000000000.0;

    }

    public static void main(String[] args) {

        int opCount = 100000;

        ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();

        double time1 = testQueue(arrayQueue, opCount);

        System.out.println("ArrayQueue, time: " + time1 + " s");

        LoopQueue<Integer> loopQueue = new LoopQueue<>();

        double time2 = testQueue(loopQueue, opCount);

        System.out.println("LoopQueue, time: " + time2 + " s");

        LinkListQueue<Integer> linkListQueue = new LinkListQueue<>();

        double time3 = testQueue(linkListQueue, opCount);

        System.out.println("LinkListQueue, time: " + time3 + " s");

    }

}

输出结果：

ArrayQueue, time: 3.069366801 s

LoopQueue, time: 0.010702659 s

LinkListQueue, time: 0.007079073 s

9.. 小练习，删除掉链表中所有值为val的节点

不使用dummyHead的实现方法

class Solution {

    public ListNode removeElements(ListNode head, int val) {

        while (head != null && head.val == val) {

            //head = head.next;

            ListNode delNode = head;

            head = head.next;

            delNode.next = null;

        }

        if (head == null) {

            return null;

        }

        ListNode prev = head;

        while (prev.next != null) {

            if (prev.next.val == val) {

                //prev.next = prev.next.next;

                ListNode delNode = prev.next;

                prev.next = delNode.next;

                delNode.next = null;

            } else {

                prev = prev.next;

            }

        }

        return head;

    }

}

使用dummyHead的实现方法：

class Solution2 {

    public ListNode removeElements(ListNode head, int val) {

        ListNode dummyHead = new ListNode(-1);

        dummyHead.next = head;

        ListNode prev = dummyHead;

        while (prev.next != null) {

            if (prev.next.val == val) {

                //prev.next = prev.next.next;

                ListNode delNode = prev.next;

                prev.next = delNode.next;

                delNode.next = null;

            } else {

                prev = prev.next;

            }

        }

        return dummyHead.next;

    }

}

使用dummyHead之后，代码变得更加简洁

10.. 递归

从本质上讲，递归，就是将原来的问题转化为更小的同一个问题；
递归举例，数组求和：

Sum(arr[0...n-1]) = arr[0] + Sum(arr[1...n-1])   <-- 转化为更小的同一个问题

Sum(arr[1...n-1]) = arr[1] + Sum(arr[2...n-1])   <-- 转化为更小的同一个问题

           ......

Sum(arr[n-1...n-1]) = arr[n-1] + Sum([])   <-- 最基本的问题

代码简单实现：

public class Sum {

    public static int sum(int[] arr) {

        return sum(arr, 0);

    }

    //计算arr[l...n)这个区间内所有数的和

    private static int sum(int[] arr, int l) {

        if (l == arr.length) {        //  <--  求解最基本问题

            return 0;

        }

        return arr[l] + sum(arr, l + 1);   //  <-- 将原问题简化为更小的问题

    }

    //测试

    public static void main(String[] args) {

        int[] arr = {1, 2, 3, 4, 5, 6, 7, 8};

        System.out.println(sum(arr));

    }

}

2.. 链表的天然递归性

通过下图，很容易理解为什么链表具有天然的递归性
用递归的思想解决删除链表中的节点的问题，原理示意图：
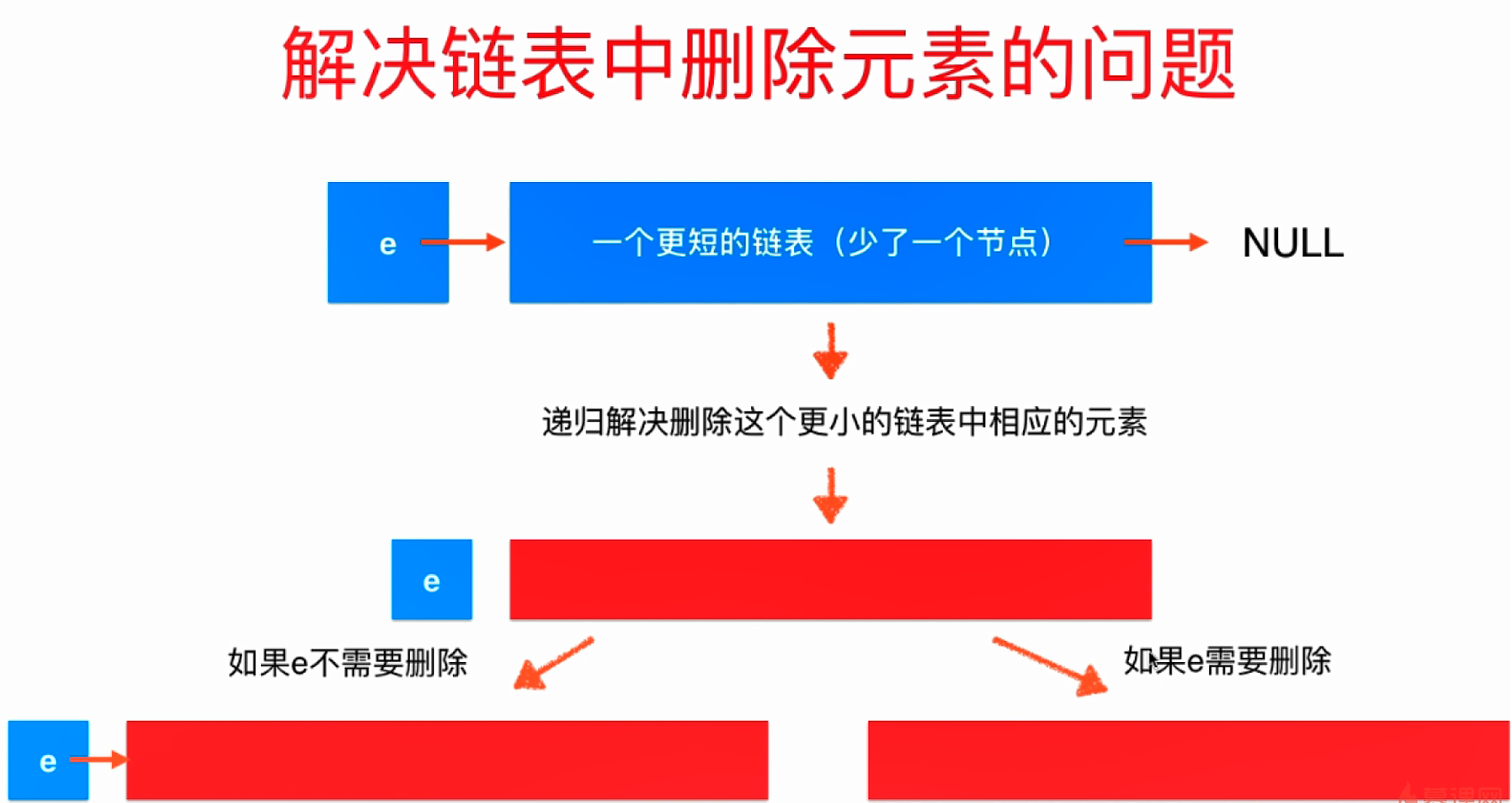
用递归实现删除链表中所有包含指定元素的节点的业务逻辑：

class Solution3 {

    public ListNode removeElements(ListNode head, int val) {

        if (head == null) {

            return null;

        }

        head.next = removeElements(head.next, val);

        //return head.val == val ? head.next : head;

        if (head.val == val) {

            return head.next;

        } else {

            return head;

        }

    }

}

第二十五篇玩转数据结构——链表（Linked List）的更多相关文章

第二十八篇玩转数据结构——堆（Heap）和有优先队列(Priority Queue)
1.. 优先队列(Priority Queue) 优先队列与普通队列的区别:普通队列遵循先进先出的原则:优先队列的出队顺序与入队顺序无关,与优先级相关. 优先队列可以使用队列的接口,只是在 ...
第二十六篇玩转数据结构——二分搜索树（Binary Search Tree）
1.. 二叉树跟链表一样,二叉树也是一种动态数据结构,即,不需要在创建时指定大小. 跟链表不同的是,二叉树中的每个节点,除了要存放元素e,它还有两个指向其它节点的引用,分别用Node l ...
第二十四篇玩转数据结构——队列（Queue）
1.. 队列基础队列也是一种线性结构: 相比数组,队列所对应的操作数是队列的子集: 队列只允许从一端(队尾)添加元素,从另一端(队首)取出元素: 队列的形象化描述如下图: 队列是一种先进 ...
第二十九篇玩转数据结构——线段树（Segment Tree）
1.. 线段树引入线段树也称为区间树为什么要使用线段树:对于某些问题,我们只关心区间(线段) 经典的线段树问题:区间染色,有一面长度为n的墙,每次选择一段墙进行染色(染色允许覆盖),问 ...
第二十五篇：在SOUI中做事件分发处理
不同的SOUI控件可以产生不同的事件.SOUI系统中提供了两种事件处理方式:事件订阅 + 事件处理映射表(参见第八篇:SOUI中控件事件的响应) 事件订阅由于直接将事件及事件处理函数连接,不存在事件分 ...
Python之路(第二十五篇) 面向对象初级：反射、内置方法
[TOC] 一.反射反射的概念是由Smith在1982年首次提出的,主要是指程序可以访问.检测和修改它本身状态或行为的一种能力(自省).这一概念的提出很快引发了计算机科学领域关于应用反射性的研究.它 ...
flask第二十五篇——控制语句
有兴趣的请加船长公众号:自动化测试实战先和大家强调一个发邮件的问题 # coding: utf-8 import smtplib from email.mime.text import MIMETe ...
第二十五篇：使用 sigaction 函数实现可靠信号
前言在前文中,讲述了一个可靠信号的示例.它分成几个步骤组成( 请参考前文 ).在 Linux 系统编程中,有个方法可以将这些步骤给集成起来,让我们使用起来更加的方便. 那就是调用 sigaction ...
SpringBoot非官方教程 | 第二十五篇：2小时学会springboot
转载请标明出处: http://blog.csdn.net/forezp/article/details/61472783 本文出自方志朋的博客一.什么是spring boot Takes an o ...

随机推荐

我的第一个原生Web Components——滑块（SingleSlider）
写着写着,就会跑偏,没错又走上了一个岔道……就是不知道这条岔道以后会不会越来越宽,有的说他是未来,有的说…… 这里不知道,也不做什么评断.减少一些重复性的工作,提高开发效率这是最根本的.说白了就是偷懒 ...
Javaweb版四则运算
显示出题界面shu01.jsp <%@ page language="java" contentType="text/html; charset=UTF-8&quo ...
openlayers 保存当前地图View为图片
/** * 保存地图为图片工具栏 */function addMapToolSavePicture() { var saveElement = document.createElement('a'); ...
linux - mysql 异常：MySQL Daemon failed to start.
报错内容 MySQL Daemon failed to start. 如果直接输入 mysql -root -p 登陆会出现 [mysql]ERROR 2002 (HY000): Can't conn ...
安卓开发中遇到java.net.SocketException: Permission denied
仅需在AndroidManifest.xml添加 <uses-permission android:name="android.permission.INTERNET" /& ...
LINUX使用SSH远程终端时，如何将运行时间长的程序在后台挂起，下次SSH登陆时继续使用同一个SHELL？
我在某个平台上购买了一个云服务器,LINUX操作系统无图形化界面,硬盘空间较小.虽然在平台上可以通过其自带网页版VNC界面登陆SHELL进而操控云主机,但是每次需要操控都得打开网页登陆进平台,然后再进 ...
selenium 百度登录
private String baseUrl="http://www.baidu.com/"; --------- @Test public void testLoginB() t ...
codeforces 1284B. New Year and Ascent Sequence（二分）
B. New Year and Ascent Sequence 题意:定义上升序列Ascent,在一组序列A中,存在1<i<j<n,使得Ai<Aj.现在给定n个序列,求n个序列 ...
接口自动化框架（Pytest，Allure，Yaml）
框架链接:https://www.jianshu.com/p/e31c54bf15ee 目前是基于他的框架做了些改动(主要是session.action()和json格式传参). 后续优化,应该主要思 ...
vue全局组件与局部组件
<!DOCTYPE html> <html> <head> <title></title> </head> <script ...

第二十五篇 玩转数据结构——链表（Linked List）

第二十五篇 玩转数据结构——链表（Linked List）的更多相关文章

随机推荐

热门专题

第二十五篇玩转数据结构——链表（Linked List）

第二十五篇玩转数据结构——链表（Linked List）的更多相关文章