链表list

Don't  lost link!

　　list与vector不同之处在于元素的物理地址可以任意。

　　为保证对列表元素访问的可行性，逻辑上互为前驱和后继的元素之间，应维护某种索引关系。这种索引关系，可抽象地理解为被索引元素的位置（position），故列表元素是“循位置访问”（call-by-position）的；也可形象地理解为通往被索引元素的链接（link），故亦称作“循链接访问”（call-by-link）。这种访问方式，如同通过你的某位亲朋，找到他/她的亲朋、亲朋的亲朋、...。注意，向量中的秩同时对应于逻辑和物理次序，而位置仅对应于逻辑次序。

　　本章的讲解，将围绕列表结构的高效实现逐步展开，包括其ADT接口规范以及对应的算法。此外还将针对有序列表，系统地介绍排序等经典算法，并就其性能做一分析和对比。

　　引入list结构的目的，就在于弥补向量结构在解决某些应用问题时，在功能和性能方面的不足。二者之间的差异，表面上是体现于对外的操作方式，但根源在于其内部存储方式的不同。

　　数据结构支持的操作无非是静态和动态两种：静态仅从中获取信息，后者则会修改数据结构的局部甚至是整体。

　　　　静态举例：

　　　　　size();  get();　 //可在常数时间内完成

　　　　　insert(); remove(); // 需要线性时间，原因在于各元素的物理地址连续

---

一、从向量到链表：

　　链表（list）是采用动态存储结构的典型策略；

　　节点（node）.各节点之间通过指针或引用彼此连接，在逻辑上构成一个线性序列。

　　L = {a0,a1,a2,....,an-1}

　　相邻节点之间彼此互称为前驱（predecessor）或后继（successor）。前驱或后继若存在，则必然唯一。

　　没有前驱/后继的节点称为首（first/front）节点/末（last/rear）节点.

　　

　　如果依然采用和向量相同的循秩访问方式，则秩越大成本越高。因此应该改用循位置访问，利用节点之间的相互引用，找到特定的节点。

---

二、ADT接口：

　　2.1  列表节点对象支持的操作接口：

 data()     当前节点所存数据对象
 pred()     当前节点前驱节点的位置
 succ()     当前节点后继节点的位置
 insertAsPred(e)     插入前驱节点，存入被引用对象e，返回新节点位置
 insertAsSucc(e)     插入后继节点，存入被引用对象e，返回新节点位置

　ListNode模板类

typedef int Rank; //秩
#define ListNodePosi(T) ListNode<T>* //列表节点位置
template <typename T> struct ListNode { //列表节点模板类（以双向链表形式实现）
// 成员
 　　T data; ListNodePosi(T) pred; ListNodePosi(T) succ; //数值、前驱、后继
 　　// 极造函数
　　ListNode() {} //针对header和trailer的构造
　　ListNode( T e, ListNodePosi(T) p = NULL, ListNodePosi(T) s = NULL)
　　　　: data(e), pred(p), succ(s) {} //默认构造器
　　// 操作接口
　　ListNodePosi(T) insertAsPred(T const& e); //紧靠当前节点之前插入新节点
　　ListNodePosi(T) insertAsSucc(T const& e); //紧随当前节点之后插入新节点
};

　　2.2  列表对象支持的操作接口：　　

　　

size()                      //报告列表的当前闺蜜（节点总数）                  列表
first()、last()           //返回首、末节点的位置                             列表
insertAsFirst(e)
insertAsLast(e)         //将e作作首、末节点插入                              列表
insertBefore(p, e)
insertAfter(p, e)       //将e当作节点p的直接前驱、后继插入              　　　　列表
remove(p)              // 删除位置p处的节点，返回其数值                  　　　　列表
disordered()           //判断所有节点是否已按非降序排列                  　　　　列表
sort()                    //调整各节点的位置，使列表按非降序排列          　　　　列表
find(e)                  // 查找目标元素e，失败时返回NULL 列表
search(e)             //查找目标元素e,返回不大于e且秩最大的节点       　　　　　　有序列表
deduplicate()       //剔除重复节点                                           列表
uniquify()            //剔除重复节点                                        有序列表
traverse()           //遍历并统一处理所有节点，处理方法由函数对象指定 　　　　　　　　列表
                                      

　list模板类：

　

 #include "listNode.h" //引入列表节点类

 template <typename T> class List { //列表模板类

 private:
 int _size; ListNodePosi(T) header; ListNodePosi(T) trailer; //规模、头哨兵、尾哨兵

 protected:
 　　void init(); //列表创建时的初始化
10　　 int clear(); //清除所有节点
11　　 void copyNodes(ListNodePosi(T), int); //复制列表中自位置p起的n项
 　　void merge(ListNodePosi(T)&, int, List<T>&, ListNodePosi(T), int); //有序列表区间归并
 　　void mergeSort(ListNodePosi(T)&, int); //对从p开始连续的n个节点归并排序
 　　void selectionSort(ListNodePosi(T), int); //对从p开始连续的n个节点选择排序
 　　void insertionSort(ListNodePosi(T), int); //对从p开始连续的n个节点插入排序

 public:
 // 极造函数
 　　List() { init(); } //默认
 　　List(List<T> const& L); //整体复制列表L
 　　List(List<T> const& L, Rank r, int n); //复制列表L中自第r项的n项
22　　 List(ListNodePosi(T) p, int n); //复制列表中自位置p起的n项
’ // 析构函数
24　　 ~List(); //释放（包含头、尾哨兵在内的）所有节点
 // 只读访问接口
 　　Rank size() const { return _size; } //规模
27　　 bool empty() const { return _size <= ; } //判空
28　　 T& operator[](Rank r) const; //重载，支持循秩访问（效率低）
 　　ListNodePosi(T) first() const { return header->succ; } //首节点位置
 　　ListNodePosi(T) last() const { return trailer->pred; } //末节点位置
31　　 bool valid(ListNodePosi(T) p) //判断位置p是否对外合法
 　　{ return p && (trailer != p) && (header != p); } //将头、尾节点等同于NULL
 　　int disordered() const; //判断列表是否已排序
 　　ListNodePosi(T) find(T const& e) const //无序列表查找
 　　{ return find(e, _size, trailer); }
 　　ListNodePosi(T) find(T const& e, int n, ListNodePosi(T) p) const; //无序区间查找
 　　ListNodePosi(T) search(T const& e) const //有序列表查找
 　　{ return search(e, _size, trailer); }
 　　ListNodePosi(T) search(T const& e, int n, ListNodePosi(T) p) const; //有序区间查找
 　　ListNodePosi(T) selectMax(ListNodePosi(T) p, int n); //在p及其前n-1个后继中选出最大者
 　　ListNodePosi(T) selectMax() { return selectMax(header->succ, _size); } //整体最大者
 // 可写访问接口
 　　ListNodePosi(T) insertAsFirst(T const& e); //将e当作首节点插入
44　　 ListNodePosi(T) insertAsLast(T const& e); //将e当作末节点插入
45　　 ListNodePosi(T) insertBefore(ListNodePosi(T) p, T const& e); //将e当作p的前驱插入
46　　 ListNodePosi(T) insertAfter(ListNodePosi(T) p, T const& e); //将e当作p的后继插入
 　　T remove(ListNodePosi(T) p); //初除合法位置p处的节点,返回被删除节点
 　　void merge(List<T>& L) { merge(first(), size, L, L.first(), L._size); } //全列表归并
 　　void sort(ListNodePosi(T) p, int n); //列表区间排序
 　　void sort() { sort(first(), _size); } //列表整体排序
 　　int deduplicate(); //无序去重
 　　int uniquify(); //有序去重
 　　void reverse(); //前后倒置（习题）
 　　// 遍历
 　　void traverse(void (*)(T&)); //遍历，依次实施visit操作（函数指针，只读或局部性修改）
 　　template <typename VST> //操作器
57　　 void traverse(VST&); //遍历，依次实施visit操作（函数对象，可全局性修改）
 }; //List

　

---

三、无序列表

　　　头节点和尾节点经过封装之后，是对外部不可见的，但是却非常有用。设置header和trailer后，first()和last()操作就可以转换为header->succ和trailer->pred。哨兵节点的引入，也使得各种算法不需要对边界退化情况做专门的处理。

　　等效的头、首、末、尾节点的秩可分别理解为-1，0，n-1,n

　

---

　

3.1构造

列表的构造即先创建一对头、尾哨兵节点，并适当设置其前驱和后继指针，构成一个双向链表。

　　

---

3.2列表的循秩访问

　　

　　其时间复杂度为 O（n）

---

3.3 查找

最坏复杂度是O(n)，线性正比于查找区间的宽度。

　　下图分别代表的是在p的n个前驱中查找元素e；在p的n个后继中查找元素e。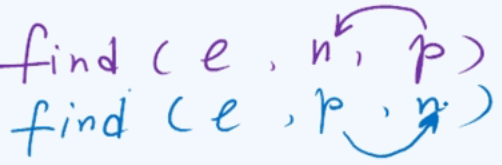

---

3.3 插入

　　微创手术：复杂度是常数。下图中的pred = x实质上是把当前节点的前驱之指向x; 如果pred->succ = x，pred =x；改为pred =x；pred->succ = x；是错误的，因为pred =x;先将当前this节点的前驱变为x，则pred->succ，就是x->succ再指向x自己。

　　

---

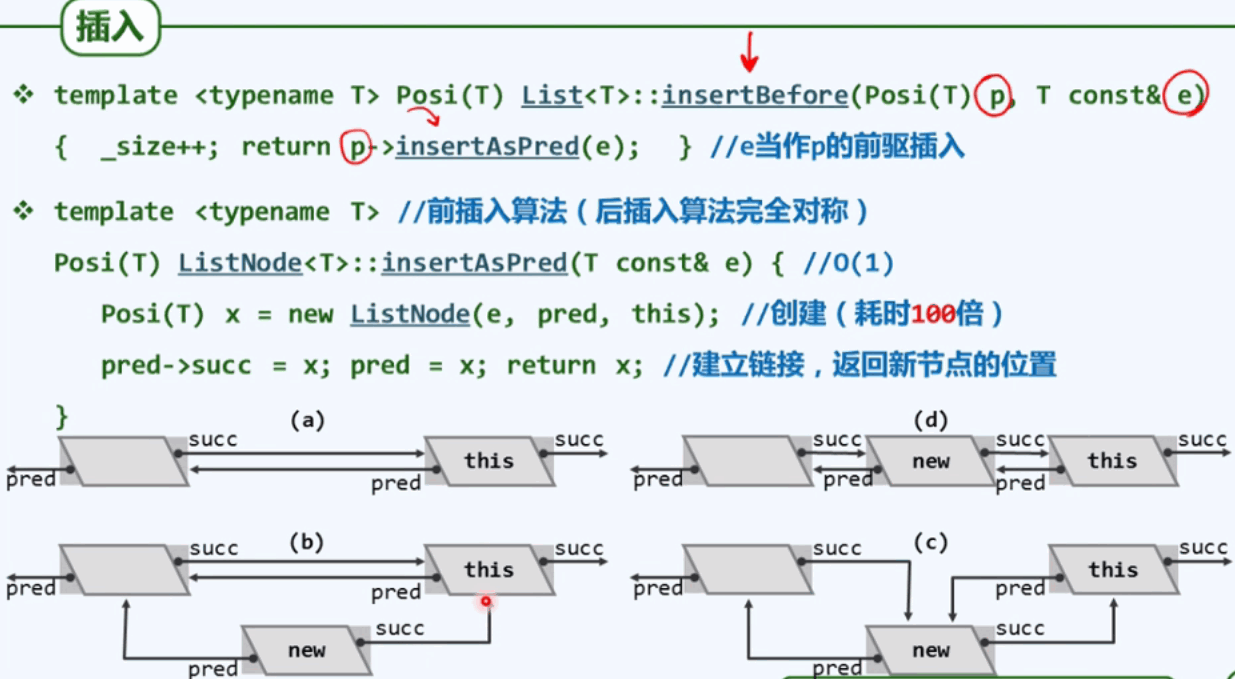
3.4 基于复制的构造

　　

从原列表中取出n个相邻的节点，并逐一作为末节点插入新列表中。　insertAsLast() 就相当于insertAsPred(trailer)。

---

3.5 删除

---

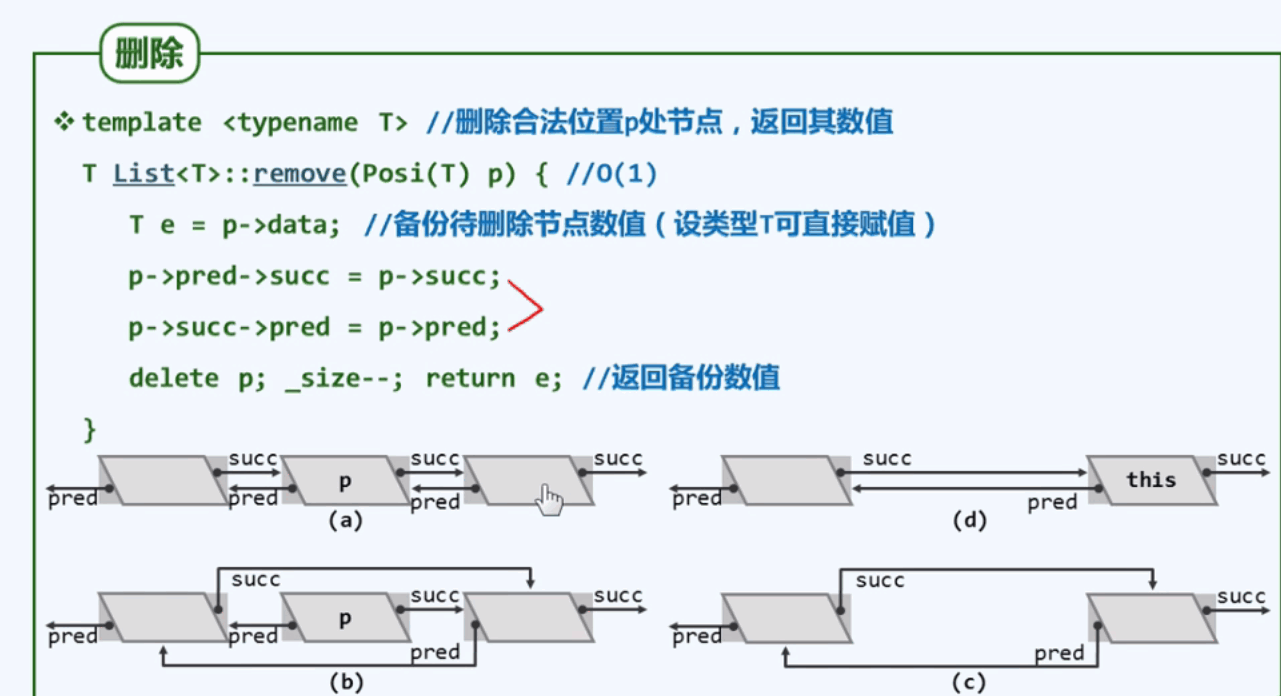
3.6 析构

• 将对外可见节点逐一删除
• 删除两个哨兵

---

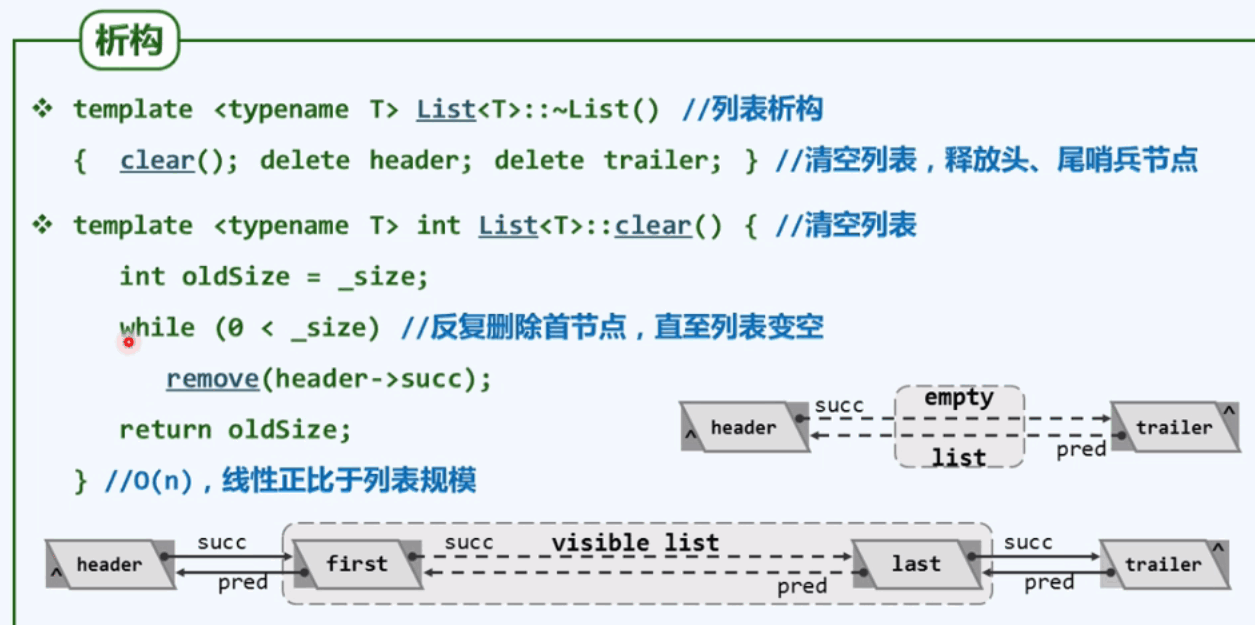
3.7 唯一化

　　

　　

---

四、有序列表

　　4.1 有序列表唯一化：

　　

---

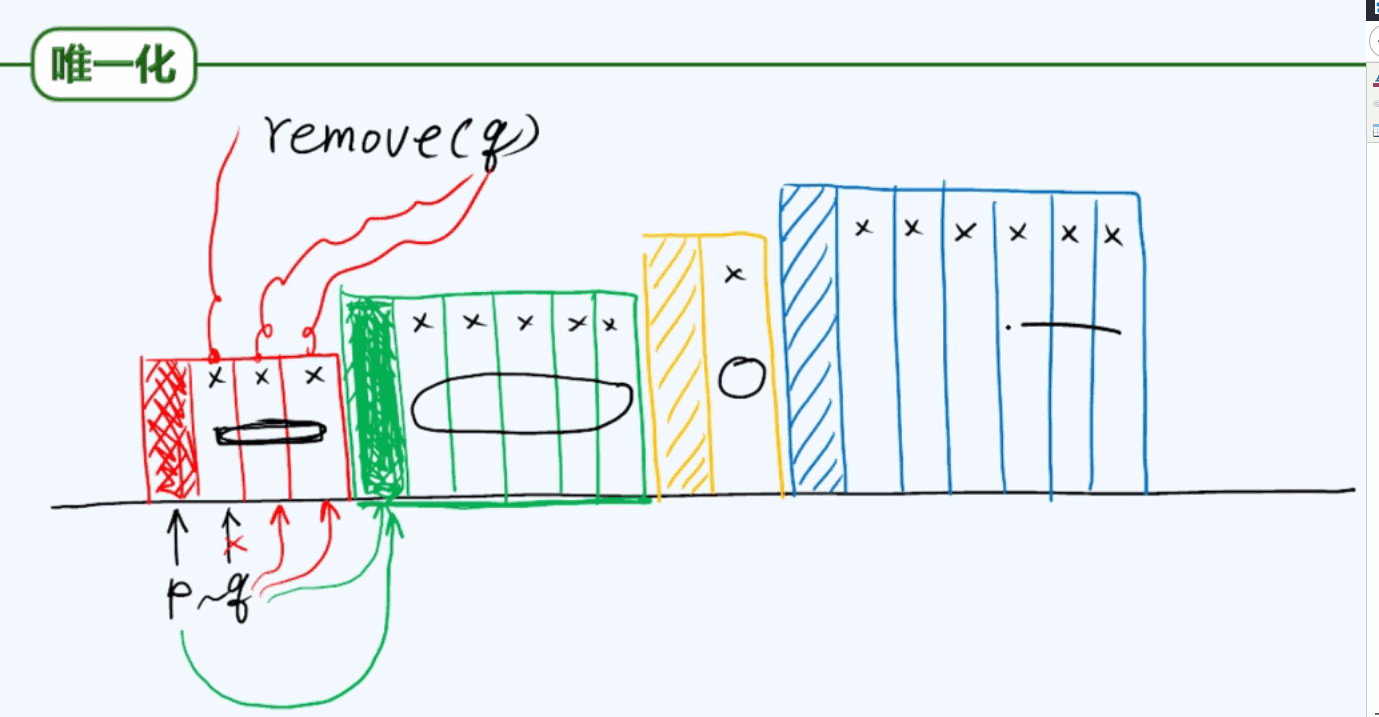
4.1 查找：

·