概率专题_概率/ 数学_基础题_ABEI

上周三讲了概率和概率dp。如果没有涉及其他综合算法，概率这种题主要是思维，先把这部分的东西写完

给个题目链接：https://vjudge.net/contest/365300#problem

HeadShoot

题目大意：玩打枪赌命游戏，已知装弹序列，且装弹和打枪的顺序同一方向，已知上一次是哑炮，打完机械会自动转一节，存活率最大，选择直接SHOOT还是ROTATE之后再射击，

思路：题目已经给了很明显的暗示，已知上一次是哑炮，说明上一次的发生的事件会影响我当前弹夹1/0表示，这是一个条件概率，

如果shoot优选，则0之后更有可能0，状态为，00，P1=00/（00+01）；

如果rotate优选，则0之后再移一位更有可能为0，有 010，000，

结果并不对，是因为题目还有一句话：“you can randomly rotate the gun’s cylinder”，这个旋转是随机的，没有规定只转一节！！！读题又先入为主了。。。

所以如果rotate优选，则此时相当于求一个混乱旋转后求概率，那么上一个是不是0这个前提后面的影响，就几乎没有了，所以，P2=0/（n）；

按照顺序，从头检查到成一个环（不是到尾），检查完整个长度，头可以从任意位置开始，检查0，01和00的个数，比较P1，P2，化成乘法即可

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<string>
 using namespace std;
 const string e="EQUAL",r="ROTATE",s="SHOOT";

 char a[];
 int x,y,t;
 int main () {
     memset(a,,sizeof(a));
     while(cin>>a) {

         x=;
         t=;
         int l=strlen(a);

         for(int i=; i<l; i++) {
             if(a[i]=='') {
                 t++;
                 int g=(i+)%l;
                 if(a[g]=='') {
                     x++;
                 }
             }
         }

         if(x*l<t*t)cout<<r;
         if(x*l==t*t)cout<<e;
         if(x*l>t*t)cout<<s;
         puts("");
         memset(a,,sizeof(a));
     }

     return ;
 }

------

Cows and Cars

大前提：主持人开的门后面只有可能是牛。主持人相当于排除了一部分牛，那剩下的工作就是算，排除之后，总的门数，含车的门数

一定换门，所以n-1-show为剩下的总数，车的数目为一个不确定的值，因为并不知道一开始选了什么，需要分情况

• 一开始是牛，那条件是cow/n，车总数不变，还是car，写成（cow/n）*car/（n-1-show）
• 一开始是车，条件是car/n，车总数-1，car-1，写成（car/n）*（car-1）/（n-1-show）

叠加两种情况即可（贝叶斯）保证精度，先乘后除

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<string>
 using namespace std;
 double cow,car,show;

 int main() {
     while(cin>>cow>>car>>show) {
         double n=cow+car;
         printf("%.5f\n",car*(car-1.0)/n/(n-1.0-show)+cow*car/n/(n-1.0-show));

     }
     return ;
 }

Joining with Friend（坑题）

题意：你会在[t1,t2]时刻到，你朋友会在[s1,s2]时刻到，两个人都停留w，问两人碰面的概率

就是很典型的几何概率，概率统计的原题，P=相交阴影面积（交集）/总面积（并集），

一开始，打算分开两条直线讨论，分类讨论阴影面积的情形，没有普遍性，算的要死掉

结果情况实在是太多了，写又写不全，实在是难受（占个坑后面看看能不能写上）

不是只有缺小三角形的情形！！！！上面那条直线可以划到下面！！WA到吐

所以可以用 上面直线下边的面积（s1+s2）-下面直线下边的面积（s1）

 #include<cstdio>
 using namespace std;
 int t,s1,s2,t1,t2,w;
 double solve(int w) {
     if(t2+w<=s1) return ;
     if(t1+w>=s2) return (s2-s1)*(t2-t1);
     if(s1-w<=t1) { // left
         if(s2-w>=t2)//right
             return 0.5*(t1+w-s1+t2+w-s1)*(t2-t1);
         else//up
             return (s2-s1)*(t2-t1)-0.5*(s2-(t1+w))*(s2-w-t1);
     } else { //down
         if(t2+w<s2) //right
             return 0.5*(t2-(s1-w))*(t2+w-s1);
         else //up
             return 0.5*(t2-(s2-w)+t2-(s1-w))*(s2-s1);
     }
 }
 int main() {
     scanf("%d",&t);
     for(int tt=; tt<=t; tt++) {
         scanf("%lf%lf%lf%lf%lf",&s1,&s2,&t1,&t2,&w);
         double ans=solve(w)-solve(-w);
         printf("Case #%d: %.8lf\n",tt,ans/((t2-t1)*(s2-s1)));
     }
 }

Standard Deviation UVA - 10886

给定一个随机数发生器, 用以下代码实现;

 unsigned long long seed;
 long double gen() {
     static const long double Z = ( long double )1.0 / (1LL<<);
     seed >>= ;
     seed &= ( 1ULL <<  ) - ;
     seed *= seed;
     return seed * Z;
 }

输入seed的初始值，你的任务是求出它得到的前n个随机数标准差，保留小数点后5位(1<=n<=10000000,0<=seed<2⁶⁴)。

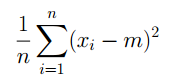
计算标准差，难点就是精度, 如果直接模拟,  用最高精度的 long double 试了一下,暴力可过

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<string>
 #include <cmath>
 using namespace std;
 typedef long long ll;
 unsigned long long seed;
 const ll M=+;
 long double gen() {
     static const long double Z = ( long double )1.0 / (1LL<<);
     seed >>= ;
     seed &= ( 1ULL <<  ) - ;
     seed *= seed;
     return seed * Z;
 }
 int N;
 int n;
 long double a[M];
 long double sum;
 long double ans;
 int main() {
     cin>>N;
     int k=;
     while(N--) {
         k++;
         memset(a,,sizeof(a));
         scanf("%d%llu",&n,&seed);
         sum=;
         ans=;
         for(int i=; i<=n; i++) {
             a[i]=gen();
             sum+=a[i];
         }
         sum/=n;
         for(int i=; i<=n; i++) {
             ans+=(a[i]-sum)*(a[i]-sum);
         }
         ans/=n;
         ans=sqrt(ans);
         printf("Case #%d: %.5Lf\n",k,ans);
     }
     return ;
 }

如果要优化, 关键是化简计算式子，因为如果按照先加再除的办法，肯定存不下，这个平方公式还是很明显的

分开算就可以了