RAID0、RAID1及RAID5的区别详解

目前已有的RAID(Redundant Array of Independent Disks,独立冗余磁盘阵列)技术有很多种，但是RAID0、RAID1、RAID5是最常见的几种方案。

1 RAID0

RAID0技术把多块(至少两块)物理硬盘设备通过软件或硬件的方式串联在一起，组成一个大的卷组，并将数据依次写入到各个物理硬盘中。这样，在最理想的情况下，硬盘设备的读写性能会提升数倍，但是若任意一块硬盘发生故障将导致整个系统的数据都受到破坏。虽然，RAID0技术能够有效的提升硬盘数据的吞吐速度，但是不具备数据备份和错误修复能力。如下图，数据被分别写入到不同的硬盘设备中，即disk1和disk2硬盘设备会被分别保存数据资料，最终实现提升读取、写入速度的效果。

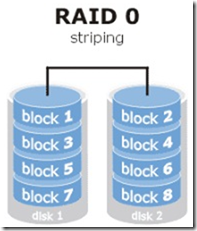
2 RAID1

尽管RAID0技术提升了硬盘设备的读写速度，但是它将数据一次写入各个物理硬盘中，也就是说，它的数据是分开存放的，其中任何一块硬盘发生故障都会损坏整个系统的数据。因此，如果生产环境对硬盘设备的读写速度没有要求，而是希望增加数据的安全性时，就需要用到RAID1技术了。

RAID1技术示意图如下图，它是把两块以上的硬盘设备进行绑定，在写入数据时，是将数据同时写入到多块硬盘设备上(可以将其视为数据的镜像或备份)。当其中某一块硬盘发生故障后，一般会立即自动以热交换的方式来恢复数据的正常使用。

RAID1技术虽然十分注重数据的安全性，但是因为是在多块硬盘设备中写入了相同的数据，因此硬盘设备的利用率下降了一半。从理论上说，如下图所示空间的真实可用率只有50%，由三块硬盘设备组成的RAID1磁盘阵列的可用率只有33%左右，以此类推。由于需要把数据同时写入两块以上的硬盘设备，这无疑也在一定程度上增大了系统计算功能的负载。

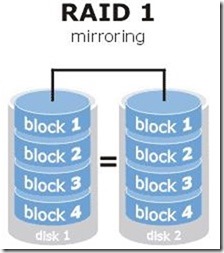
3 RAID5

RAID5技术是把硬盘设备的数据奇偶校验信息保存到其他硬盘设备中。RAID5磁盘阵列组中数据的奇偶校验信息并不是单独保存到某一块磁盘设备中，而是存储到除自身以外的其他每一块设备上，这样的好处是其中任何一个设备损坏后不至于出现致命缺陷。下图“parity”部分存放的就是数据的奇偶校验信息，换句话说，就是RAID5技术实际上没有备份磁盘中的真实数据信息，而是当硬盘设备出现问题后通过奇偶校验信息来尝试重建损坏的数据。RAID5这样的技术特性“妥协”的兼顾了硬盘设备的读写速度、数据安全性与存储成本问题。

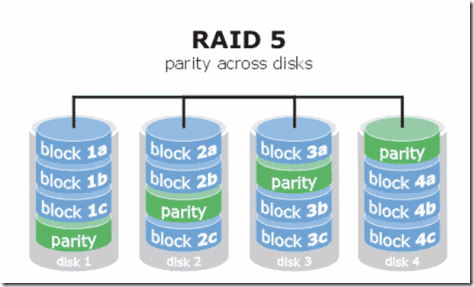
注：

奇偶校验的底层运算基础就是异或运算，但是在通俗的人类理解，应该是奇偶校验更好理解

100000110 

100000010

这两个数据在人类看来，就是在倒数第三位一个是0一个是1的区别。假设现在存储这一数据的硬盘坏了，数据就会变成：

100000X10

100000X10

那么，怎么通过奇偶校验还原这个数据呢？

人类的思维就是通过这个数据加起来一共有多少个1或者多少个0，然后补回去就是了，但是这样的话，校验的数据就分别变成3跟2（数据中1的个数），但这样是无法通过二进制不增加数据长度的办法实现的。所以奇偶校验就提供了一个更好的方法，3是奇数，所以校验数据是1，2是偶数，校验数据就是0，通过这样，在原数据只丢一位数据的前提下，完全可以运算得出原数据。

4 RAID10

鉴于RAID5技术是因为磁盘设备的成本问题对读写速度和数据的安全性能而有了一定的妥协，但是在企业里更在乎的还是数据本身的价值而非硬盘的价格，因此在生产环境中推荐使用RAID10技术。

RAID10即RAID0+RAID1的一个组合体。如下图所示，RAID10技术需要至少4块硬盘来组建，其中先分别两两制作成RAID1磁盘阵列，以保证数据的安全性；然后再对两个RAID1次哦按阵列实施RAID0技术，进一步提高硬盘设备的读写速度。这样从理论上讲，只要坏的不是同一组中的所有磁盘，那么最多可以损坏50%的硬盘设备而不丢失数据。由于RAID10技术继承了RAID0的高速写速度和RAID1的数据安全性，在不考虑成本的情况下RAID10的性能都超过了RAID5，因此当前成为广泛使用的一种存储技术。

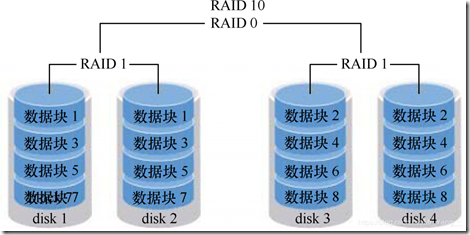
附：读写速度数据对比

威铁马硬盘盒 + 2块7200转 HGST 4T 硬盘，win10系统+usb进行读写测试

1）single模式（不做raid）：

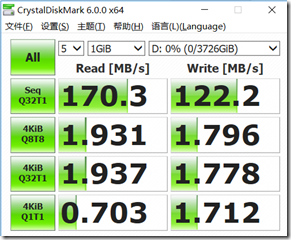
2）raid0

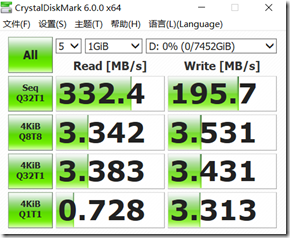
3）raid1

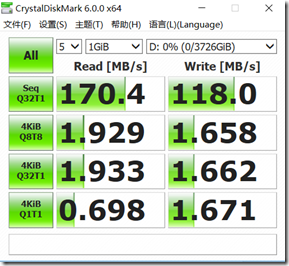
参考原文：https://blog.csdn.net/Mr_Yang__/article/details/85228465