poj1149 经典建模














http://wenku.baidu.com/view/0ad00abec77da26925c5b01c.html 以上内容均为转载
#include<queue>
#include<vector>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=;
const int INF=;
vector<int>G[];
bool mp[N][N],used[];
int tot,head[N],dis[N],st,ed,val[],sum[N];
struct node{
int to,next,w;
}e[N*N*];
void init(){
tot=;
memset(head,-,sizeof(head));
}
void add(int u,int v,int w){
e[tot].to=v;
e[tot].w=w;
e[tot].next=head[u];
head[u]=tot++;
}
bool bfs(){
memset(dis,-,sizeof(dis));
queue<int>Q;
Q.push(st);
dis[st]=;
while(!Q.empty()){
int u=Q.front();
Q.pop();
for(int i=head[u];i+;i=e[i].next){
int v=e[i].to;
if(dis[v]==-&&e[i].w>){
dis[v]=dis[u]+;
if(v==ed) return true;
Q.push(v);
}
}
}
return false;
}
int dfs(int s,int low){
if(s==ed||low==) return low;
int ans=low,a;
for(int i=head[s];i+;i=e[i].next){
int v=e[i].to;
if(dis[v]==dis[s]+&&e[i].w>&&(a=dfs(v,min(ans,e[i].w)))){
ans-=a;
e[i].w-=a;
e[i^].w+=a;
if(!ans) return low;
}
}
if(low==ans) dis[s]=-;
return low-ans;
}
int main(){
int n,m,x,num;
while(scanf("%d%d",&n,&m)!=EOF){
st=;ed=m+;
memset(sum,,sizeof(sum));
for(int i=;i<=n;++i) G[i].clear();
for(int i=;i<=n;++i) scanf("%d",val+i);
memset(used,,sizeof(used));
init();
for(int i=;i<=m;++i) {
scanf("%d",&num);
while(num--){
scanf("%d",&x);
if(!used[x]) {used[x]=;sum[i]+=val[x];}
G[x].push_back(i);
}
scanf("%d",&x);
add(i,ed,x);
add(ed,i,);
}
memset(mp,,sizeof(mp));
for(int i=;i<=n;++i){
for(int j=;j<(int)G[i].size();++j){
if(!j&&!mp[][G[i][j]]) {
mp[G[i][j]][]=mp[][G[i][j]]=;
add(,G[i][j],sum[G[i][j]]);
add(G[i][j],,);
}
else if(!mp[G[i][]][G[i][j]]) {
add(G[i][],G[i][j],INF);
add(G[i][j],G[i][],);
mp[G[i][]][G[i][j]]=;
}
}
}
int ans=;
while(bfs()) ans+=dfs(,INF);
printf("%d\n",ans);
}
}
poj1149 经典建模的更多相关文章
- HDU1045(二分图经典建模)
Fire Net Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Su ...
- Wolsey“强整数规划模型”经典案例之一单源固定费用网络流问题
Wolsey“强整数规划模型”经典案例之一单源固定费用网络流问题 阅读本文可以理解什么是“强”整数规划模型. 单源固定费用网络流问题见文献[1]第13.4.1节(p229-231),是"强整 ...
- 「国庆训练&知识学习」图的最大独立集与拓展(Land of Farms,HDU-5556)
题意 一个\(N*M\)的矩阵,其中"."代表空地,"0-9"代表古代建筑,我们如果选择了一个编号的古代建筑想要建立,那么对应就要将全部该编号的建筑建立起来,如 ...
- 【bzoj1976】[BeiJing2010组队]能量魔方 Cube 网络流最小割
题目描述 一个n*n*n的立方体,每个位置为0或1.有些位置已经确定,还有一些需要待填入.问最后可以得到的 相邻且填入的数不同的点对 的数目最大. 输入 第一行包含一个数N,表示魔方的大小. 接下来 ...
- 网络流24题:P2762 太空飞行计划问题
P2762 太空飞行计划问题 题目背景 题目描述 W 教授正在为国家航天中心计划一系列的太空飞行.每次太空飞行可进行一系列商业性实验而获取利润.现已确定了一个可供选择的实验集合E={E1,E2,…,E ...
- BZOJ3532 [Sdoi2014]Lis 【网络流退流】
题目 给定序列A,序列中的每一项Ai有删除代价Bi和附加属性Ci.请删除若 干项,使得4的最长上升子序列长度减少至少1,且付出的代价之和最小,并输出方案. 如果有多种方案,请输出将删去项的附加属性排序 ...
- UVA11082 Matrix Decompressing 最大流建模解矩阵,经典
/** 题目:UVA11082 Matrix Decompressing 链接:https://vjudge.net/problem/UVA-11082 题意:lrj入门经典P374 已知一个矩阵的行 ...
- poj1149最大流经典构图神题
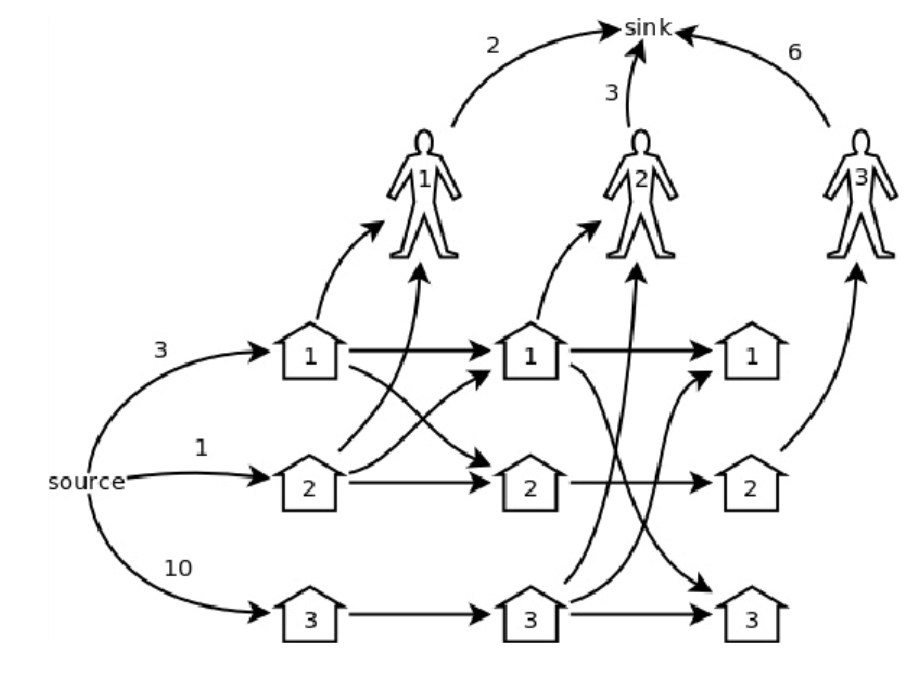
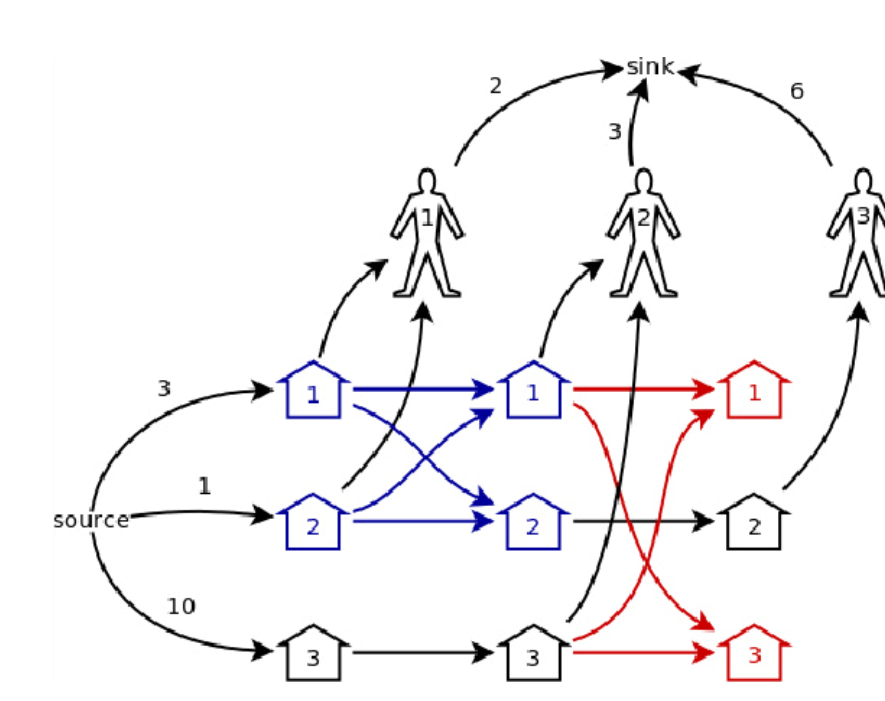
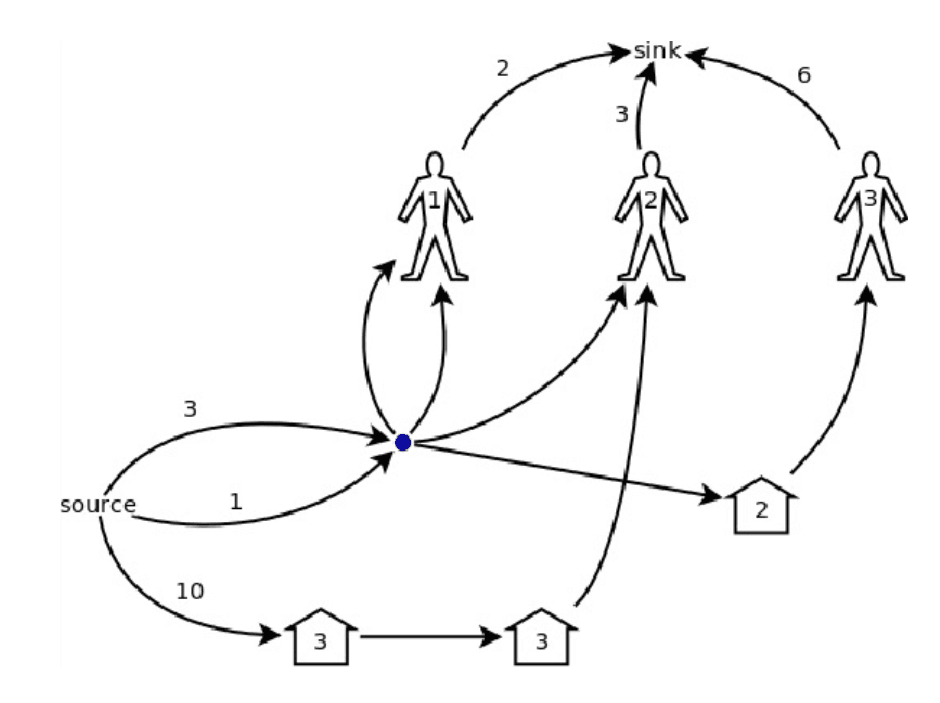
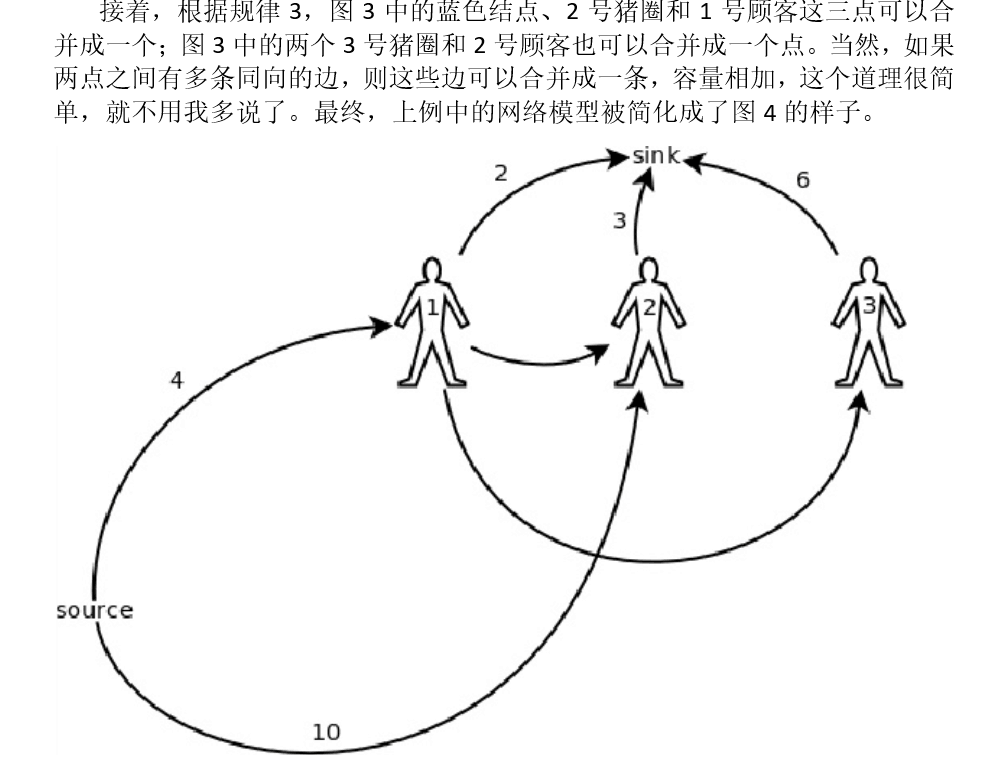
题意:n个顾客依次来买猪,有n个猪房,每个顾客每次可以开若干个房子,买完时,店主可以调整这位顾客 开的猪房里的猪,共m个猪房,每个猪房有若干猪,求最多能卖多少猪. 构图思想:顾客有先后,每个人想要的猪 ...
- 余胜威《MATLAB数学建模经典案例实战》2015年版
内容介绍 本书全面.系统地讲解了数学建模的知识.书中结合历年全国大学生数学建模竞赛试题,采用案例与算法程序相结合的方法,循序渐进,逐步引导读者深入挖掘实际问题背后的数学问题及求解方法.在本书案例的分析 ...
随机推荐
- 徐州I
#include<bits/stdc++.h> using namespace std; #define rep(i,a,b) for(int i=a;i<=b;++i) #defi ...
- 虚拟机 VMware Workstation Pro 15.5.0 及永久激活密钥
虚拟机 VMware Workstation Pro 15.5.0 及永久激活密钥 虚拟机下载地址:https://download3.vmware.com/software/wkst/file/VM ...
- Ubuntu登陆时忘记密码怎么办
有时候由于各种原因,用户会忘记自己登陆Ubuntu的登陆密码,这个时候我们能怎么办呢? 第一步:先重启电脑,开机时长按shift键,进入grub菜单: 第二步:按“e”键编辑启动项,显示如下图,将下图 ...
- Netty随记之ChannelInboundHandlerAdapter、SimpleChannelInboundHandler
ChannelInboundHandlerAdapter ChannelInboundHandlerAdapter是ChannelInboundHandler的一个简单实现,默认情况下不会做任何处理, ...
- layui表格参数
layui表格对数据进行用table样式展现 举个例子: <!doctype html> <html> <head> <meta charset=" ...
- elementUI字体图标不显示问题
原文链接: 点我 自己搭建的Vue项目,没有使用vue-cli,引入elementUI时提示字体图标404,找不到文件,如下错误: GET http://localhost:9090/WEB-INF/ ...
- 数学--数论--Hdu 5793 A Boring Question (打表+逆元)
There are an equation. ∑0≤k1,k2,⋯km≤n∏1⩽j<m(kj+1kj)%1000000007=? We define that (kj+1kj)=kj+1!kj! ...
- 3) drf 框架生命周期 请求模块 渲染模块 解析模块 自定义异常模块 响应模块(以及二次封装)
一.DRF框架 1.安装 pip3 install djangorestframework 2.drf框架规矩的封装风格 按功能封装,drf下按不同功能不同文件,使用不同功能导入不同文件 from r ...
- thinkphp 5.x~3.x 文件包含漏洞分析
漏洞描述: ThinkPHP在加载模版解析变量时存在变量覆盖的问题,且没有对 $cacheFile 进行相应的消毒处理,导致模板文件的路径可以被覆盖,从而导致任意文件包含漏洞的发生. 主要还是变量覆盖 ...
- C. Game with Chips(陷阱暴力题)
\(为什么说这是个陷阱呢??\) \(因为不管你脑洞多大,数学多好,都发现会束手无策\) \(每移动一次不知道往哪个方向,不知道先访问哪个点,同时要记录所有点的坐标,记录每个点是否访问过目标点.... ...
