浅谈字典树Trie

\(\;\)

本文是作者学习《算法竞赛进阶指南》的所得，有些语言是摘自其中。

\(\;\)

基础知识

定义

\(\;\)

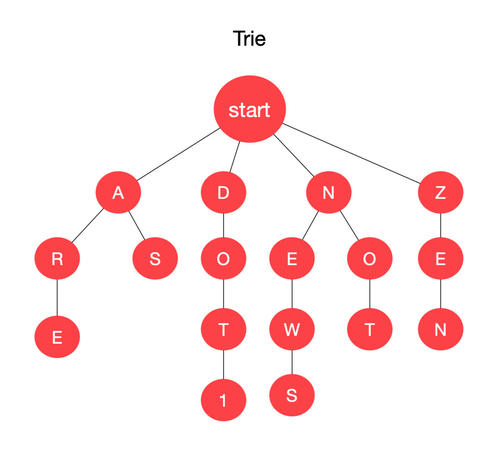
字典树（Trie）：是一种支持字符串查询的多叉树结构。其中的每个节点，都有字符指针，指向了它的若干个儿子。

如图：



\(\;\)

空间复杂度

\(\;\)

\(O(NC)\)

其中\(N\)是节点个数，\(C\)是字符集的大小。

\(\;\)

Insert

\(\;\)

找到这个字符串在Trie中的最大前缀，把前缀后面的部分插到这个节点的后面

code

void Insert(char* str,int root)
{
    int len = strlen(str);
    for(int i=0;i<len;i++)
    {
        int c = str[i] - 'a'; //转成数字存储
        if(!trie[root][c]) trie[root][c] = ++idx; //若指针为空，就新建一个指向c的指针
        root = trie[root][c]; //然后继续往下遍历
    }
}

Query

\(\;\)

不断地通过字符指针向下检索。直到字符指针为空，或者查询完毕为止。

code

bool Query(char* str,int root)
{
    int len = strlen(str);
    for(int i=0;i<len;i++)
    {
        int c = str[i] - 'a';
        root = trie[root][c];
        if(root == 0) return false; //若指针为空，则字符串不存在
    }
    return true;
}

Problem 1

\(\;\)

题意

\(\;\)

有\(n\)个字符串\(S_1,S_2,\cdots,S_n\)。接下来有\(M\)次询问，每次询问给定一个字符串\(T\)，求\(S_1-S_n\)有多少个字符串是\(T\)的前缀。

其中输入字符串的总长度不超过\(10^6\)

\(\;\)

做法

\(\;\)

我们把\(S_1,S_2,\cdots,S_n\)这些字符串插到一棵字典树里。(参考Insert操作)。在插入的同时，顺便在每个节点上记录一个\(cnt\)，表示多少个字符串在这里结尾。

然后对于每次询问，我们在字典树中查询这个字符串\(T\)。在查询过程中，累加上节点上\(cnt\)所得结果就是答案。

其实相当于对\(T\)的每个前缀算一下贡献。

\(\;\)

code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1000010;
char str[N];
int n, m, tree[N][26], root, idx, end_cnt[N];
void Insert(char* str,int root)
{
    int len = strlen(str);
    for(int i=0;i<len;i++)
    {
        int c = str[i] - 'a';
        if(!tree[root][c]) tree[root][c] = ++idx;
	root = tree[root][c];
    }
    end_cnt[root] ++;
}
int Query(char* str,int root)
{
    int len = strlen(str), res = 0;
    for(int i=0;i<len;i++)
    {
	int c = str[i] - 'a';
	root = tree[root][c];
	if(root == 0) break;
	res += end_cnt[root];
    }
    return res;
}
int main()
{
    cin >> n >> m;
    while( n-- )
    {
        scanf("%s",str);
	Insert(str,root);
    }
    while( m -- )
    {
	scanf("%s",str);
	printf("%d\n",Query(str,root));
    }
    return 0;
}

\(\;\)

Problem 2

\(\;\)

题意

\(\;\)

给定一颗\(n\)个节点的树，树的每条边都有一个权值。从中选择两个点\(x,y\)。使得\(x\)到\(y\)的路径上的所有边权\(xor\)(异或)起来，得到的结果最大是多少？

\(n\leq 10^5\)，边权\(\leq 2^{31}-1\)

\(\;\)

转化

\(\;\)

单看路径不太好搞，但是有一个比较套路的性质。

我们定义\(d(x)\)表示\(x\)到根节点\(root\)上边权的异或值

可以发现：对于两个点\(x\)到\(y\)路径上的异或值\(=d(x)\;xor\;d(y)\)，因为它们\(LCA\)以上的点都被异或没了（\(a\;xor\;a=0\)）。

因此我们要算的其实就是:在\(d(1),d(2),\cdots,d(n)\)中选出两个数，使得它们的异或值最大。

\(\;\)

01字典树

\(\;\)

我们可以把每个数拆分成二进制，因此，我们可以把数看作一个长度为\(31\)的\(01\)串(数值较小时在前补前导\(0\))，插到字典树中(其中最低二进制位为叶子节点)。

接下来，我们对于\(d(i)\)在\(Trie\)中进行一次与\(Query\)类似的操作。由于\(xor\)运算相同得\(0\)，不同得\(1\)的性质，每次我们都贪心往与当前位相反的指针向下访问。若与当前位相反的指针为空，则只好访问与\(d(i)\)当前位相同的指针。根据这样的贪心策略，我们可以找到最优解。

\(\;\)

code

#include <cstdio>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 100010, M = 3000010;
#define PII pair<int,int>
int n, son[M][2], root, idx, d[N], res;
vector<PII> G[N];
void Dfs(int u,int fa)
{
    for(int i=0;i<G[u].size();i++)
    {
        int v = G[u][i].first;
        if(v == fa) continue;
        d[v] = G[u][i].second ^ d[u];
        Dfs(v,u);
    }
}
void Insert(int root,int x)
{
    for(int i=30;~i;i--)
    {
        int s = x >> i & 1;
        if(!son[root][s]) son[root][s] = ++idx;
        root = son[root][s];
    }
}
int Query(int root,int x)
{
    int res = 0;
    for(int i=30;~i;i--)
    {
        int s = x >> i & 1;
        if(son[root][s ^ 1])
        {
            res += 1 << i;
            root = son[root][s ^ 1];
        }
        else
        {
            root = son[root][s];
        }
    }
    return res;
}
int main()
{
    cin >> n;
    for(int i=1;i<n;i++)
    {
        int u, v, w;
        scanf("%d%d%d",&u,&v,&w);
        G[u].push_back( make_pair (v, w) );
        G[v].push_back( make_pair (u, w) );
    }
    Dfs(1,0);
    for(int i=1;i<=n;i++)Insert(root, d[i]);
    for(int i=1;i<=n;i++)res = max(res, Query(root, d[i]));
    printf("%d",res);
    return 0;
}

可持久化Trie

\(\;\)

相比于只能维护最新状态的普通的数据结构，可持久化的数据结构可以知道任意时间的历史状态。

它具体是如何实现的？

朴素想法：在每次修改后把整个数据结构\(copy\)一遍。但这样的时间、空间复杂度都是\(O(nm)\)的。(\(n\)为数据结构大小，\(m\)为版本个数)

而可持久化提供了我们一种思想：每次只记录发生变化的部分，这样时间复杂度并无增加，而空间复杂度只会增加与时间同级的规模。

例如：线段树，每次修改至多变化\(log(n)\)个节点，则空间就只会增加\(log(n)\)

下面给大家模拟一下可持久化Trie的过程。

\(\;\)

模拟过程

\(\;\)

1.设当前根节点为\(root\)，令\(p=root,idx=0\)

2.建立一个新的节点\(q\)，令\(root'=q\)

3.若\(p\)不为空，则对于每种字符\(c\)，令\(trie[q][c]=trie[p][c]\)

4.建立一个新的节点：\(trie[q][str_i]=++idx\)。

(而3，4操作其实就是除了字符\(str_i\)外，其他的信息完全相同)

5.令\(p=trie[p][str_i],q=trie[q][str_i]\)(向下遍历)

然后重复\(3-5\)的步骤，直到\(q\)到字符串末尾

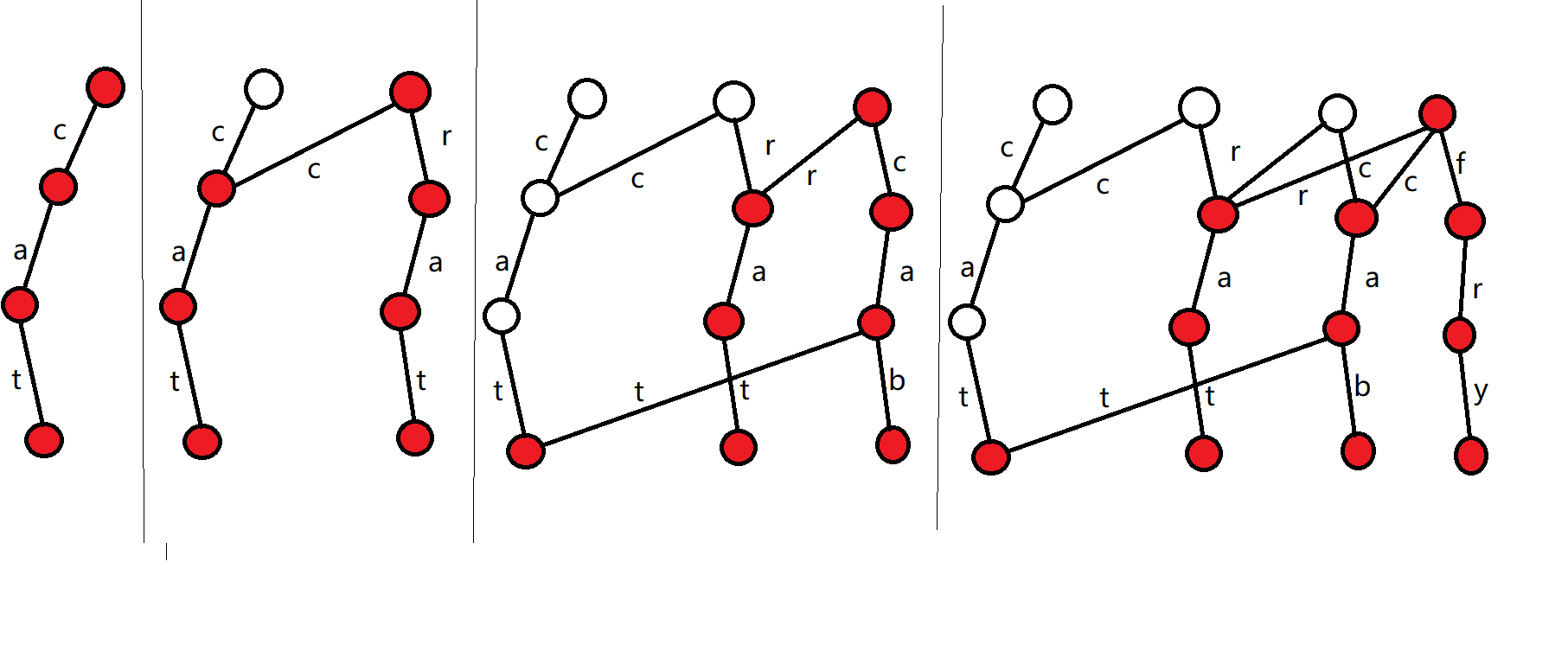
图中展示了在可持久化Trie中依次插入\(cat,rat,cab,fry\)的过程。

通过这样的操作，我们就可以得到4个版本的Trie了。



\(\;\)

\(\;\)

Problem 1

\(\;\)

给定一个非负整数序列 \(a\)，初始长度为\(n\)。

有 \(m\) 个操作，有以下两种操作类型：

\(A\;\;x\)：添加操作，表示在序列末尾添加一个数 \(x\)，序列的长度加一。

\(Q\;\;l\;\;r\;\;x\)：询问操作，你需要找到一个位置 \(p\)，满足\(l\leq p\leq r\)，使得：\(a[p] \;xor \;a[p+1]\;xor\; \cdots \;xor\; a[n] \;xor\;x\) 尽可能的大，输出最大值是多少。

\(n,m\leq 3\times 10^5,a[i]\leq 10^7\)

\(\;\)

前缀和

\(\;\)

一般这种一段区间的异或和我们都用前缀和的思路来做。

令\(s_i=a[1]\;xor \;\cdots \;xor\;a[i]\)，显然\(a[l] \;xor \;a[l+1]\;xor\; \cdots \;xor\; a[r]=s_{l-1}\;xor\;s_r\)

令\(k=s_n\;xor\;x\)

也就是说：我们要找到一个\(p\;(l-1\leq p\leq r-1)，\)使得\(s_p\;xor\;k\)最大。

如果不考虑\(l-1,r-1\)的限制，那么这道题就是我们前面讲的那个\(Problem\;2\)。

但是现在有限制，如何操作?

\(\;\)

可持久化

\(\;\)

这就要用到可持久化的精髓了。既然\(p\leq r-1\)，则\(p\)一定是第\(r-1\)个版本中的\(s_i\)。

右端点处理完了，左端点？

由于我们不可以取\(<l-1\)的\(s_i\)，则我们记录一个信息\(maxid[u]\)，表示\(Trie\)中以\(u\)为根的子树中以某个二进制数为结尾的\(s_i\)的\(i\)最大是多少。

例如：以\(u\)为根的子树中，有以\(s_1,s_3,s_7\)为结尾的节点，则\(maxid[u]=7\)。

那么，在贪心找相反的指针时，如果这颗子树的\(maxid\)大于\(\geq l-1\)，说明其中至少有一个数的编号是\(\geq l-1\)的，我们就可以往其中遍历，否则只能往相同的指针方向走了。

由于插入的时候要维护\(maxid\)这个信息，所以我们采用递归的方式来写。

时间复杂度：\(O((n+m)\;log\;10^7)\)

\(\;\)

code

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 600010, M = N * 24;
int n, q, s[N], tree[M][2], root[N], idx, max_id[M];
inline int read(){
   int s=0,w=1;
   char ch=getchar();
   while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}
void Insert(int Bits, int Now, int Last, int t)
{
	if(Bits < 0)
	{
		max_id[Now] = t;
		return;
	}
	int v = s[t] >> Bits & 1;
	if(Last) tree[Now][v ^ 1] = tree[Last][v ^ 1];
	tree[Now][v] = ++idx;
	Insert(Bits - 1,tree[Now][v],tree[Last][v],t);
	max_id[Now] = max(max_id[tree[Now][0]],max_id[tree[Now][1]]);
}
int Query(int Now, int k, int L)
{
	for(int i=23;i>=0;i--)
	{
		int v = k >> i & 1;
		if(tree[Now][v ^ 1] && max_id[tree[Now][v ^ 1]] >= L)Now = tree[Now][v ^ 1];
		else Now = tree[Now][v];
	}
	return k ^ s[max_id[Now]];
}
int main()
{
	n = read(); q = read();
	root[0] = ++idx;
	Insert(23,root[0],0,0);
	for(int i=1;i<=n;i++)
	{
		s[i] = read();
		s[i] ^= s[i - 1];
		root[i] = ++idx;
		Insert(23, root[i], root[i-1], i);
	}
	while( q-- )
	{
		char op[2];
		scanf("%s",op);
		if(op[0] == 'A')
		{
			n ++;
			s[n] = read();
			s[n] ^= s[n - 1];
			root[n] = ++idx;
			Insert(23, root[n], root[n - 1], n);
		}
		else
		{
			int l, r, x;
			l = read(); r = read(); x = read();
			int t = s[n] ^ x;
			printf("%d\n",Query(root[r - 1], t, l - 1));
		}
	}
	return 0;
}