数据结构之栈—强大的四则复杂运算计算器(超过windows自带的科学计算器)【中缀转后缀表达式】

比windows自带计算器还强的四则复杂运算计算器！

实测随机打出两组复杂算式：-7.5 * 6 / ( -2 + ( -6.5 -  -5.22 ) )与   7.5+-3*8/(7+2)

windows的科学计算器计算结果分别为：-3.28（错误）和9(错误)，全错！！！不信的小伙伴可以口算下。

正确答案是：13.71951219512195和4.833333333333334

中缀表达式转后缀表达式并进行计算的计算器（支持带负号、括号和小数的加减乘除运算）

一步一步来

假设有这样一个算式：-7.5 * 6 / ( -2 + ( -6.5 -  -5.22 ) )

我们先要将这一字符串进行分析，哪些是数字，哪些是符号。（比如：-7.5就是数字）

具体代码如下：

---

// 表达式转中缀表达式(支持小数点，负数，小括号)
    public List<String> getList(String expression) {
        List<String> exp = new ArrayList<String>();//存放解析后的中缀表达式
        String merge = "";
        int index = 0;
        char ch, ch1 = 0;
        boolean flag = false;
        expression = expression.replace(" ", "");
        while (index != expression.length()) {
            ch = expression.substring(index, index + 1).charAt(0);
            merge += ch;
            if (index < expression.length() - 1) {// 防止下标越界
                ch1 = expression.substring(index + 1, index + 2).charAt(0);
                if (isOper(ch1)) {
                    exp.add(merge);
                    merge = "";
                    flag = false;
                } else if (isOper(ch)) {
                    if (flag == false && exp.size() > 0) {
                        exp.add(merge);
                        merge = "";
                        flag = false;
                    }
                }
                if (ch == '(' && ch1 == '-' || isOper(ch) && ch1 == '-')
                    flag = true;
            }
            index++;
        }
        exp.add(merge);
        return exp;
    }

接下来就是重头戏了！！！中缀表达式—>后缀表达式思路分析图：

---

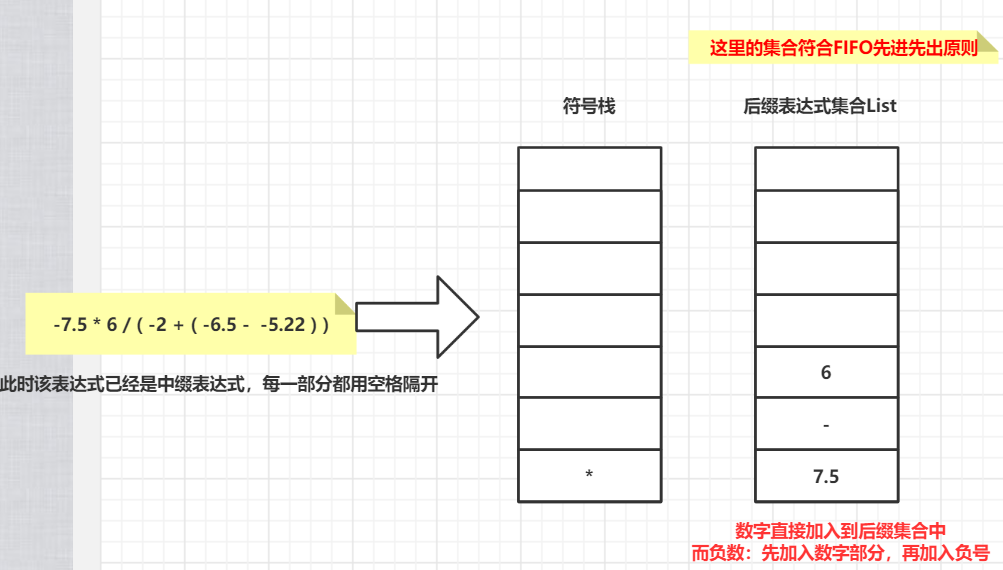
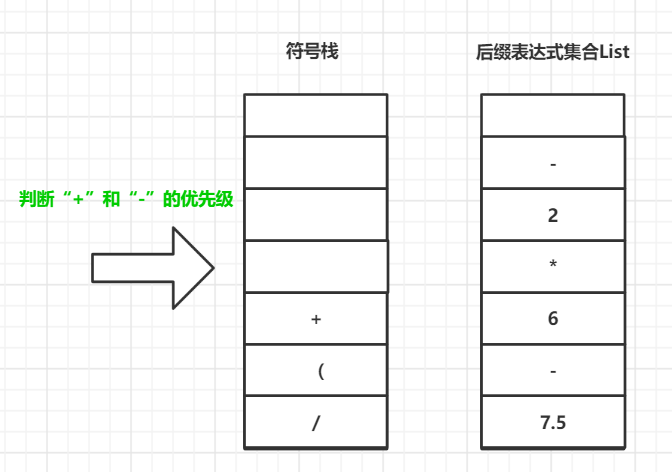
遵循以上红字规则处理第二个左括号“（”后面的元素，直到右括号“）”

---

将符号栈中所有符号弹出加入到集合List中，直到碰到一个与右括号匹配的左括号

---

以上就是从中缀表达式转换到后缀表达式的图解！得：后缀表达式为：7.5  -  6  *  2  -  6.5  -  5.22  -  -  +  /

下面是代码详解：

---

 // 中缀表达式转后缀表达式(有个记录负号索引的全局变量minus，方便计算)
    public List<String> toRPN(String expression) {
        List<String> list=getList( expression );
        List<String> rPN=new ArrayList<String>();// 用于存放后缀表达式
        Stack<String> exp=new Stack<String>();// 用于操作判断符号
        minus=new ArrayList<>();
        for (String s : list) {// 将中缀表达式每个元素list遍历
            if (isOper( s )) {// 如果字符串是+-*/
                if (exp.isEmpty())// 如果栈是空，那么就直接入栈
                    exp.push( s );//-7.5*6/(-2+(-6.5- -5.22))
                else if (priority( s ) <= priority( exp.peek() )) {// 如果栈里面有运算符，那么就和栈顶运算符比较优先级
                    rPN.add( exp.pop() );// 当前运算符优先级小于栈顶运算符，就把栈顶运算符弹出加入到后缀表达式rPN列表中
                    exp.push( s );// 然后压入当前运算符
                } else
                    exp.push( s );

            } else if (s.equals( ")" )) {// 如果当前字符串是‘)’那么就将栈顶字符串加入add到List rPN中，直到栈顶字符串为"("
                while (!exp.peek().equals( "(" )) {
                    rPN.add( exp.pop() );
                }
                exp.pop();// 一定要记得将左括号(弹出去，代表一对小括号完成计算
            } else if (s.equals( "(" ))
                exp.push( s );// 如果是左括号就直接入栈
            else {// 否则就是数字，直接加入rPN中
                if (s.charAt( 0 ) == '-') {
                    rPN.add( s.substring( 1, s.length() ) );
                    rPN.add( "" + s.charAt( 0 ) );
                    minus.add( rPN.size() - 1 );//全局变量minus负号索引list集合
                } else
                    rPN.add( s );
            }
        }
        while (!exp.isEmpty()) {// 最后扫描完list后，将栈exp中的字符串依次加入到rPN后缀表达式列表中
            rPN.add( exp.pop() );
        }
        return rPN;
    }

计算后缀表达式思路分析图：

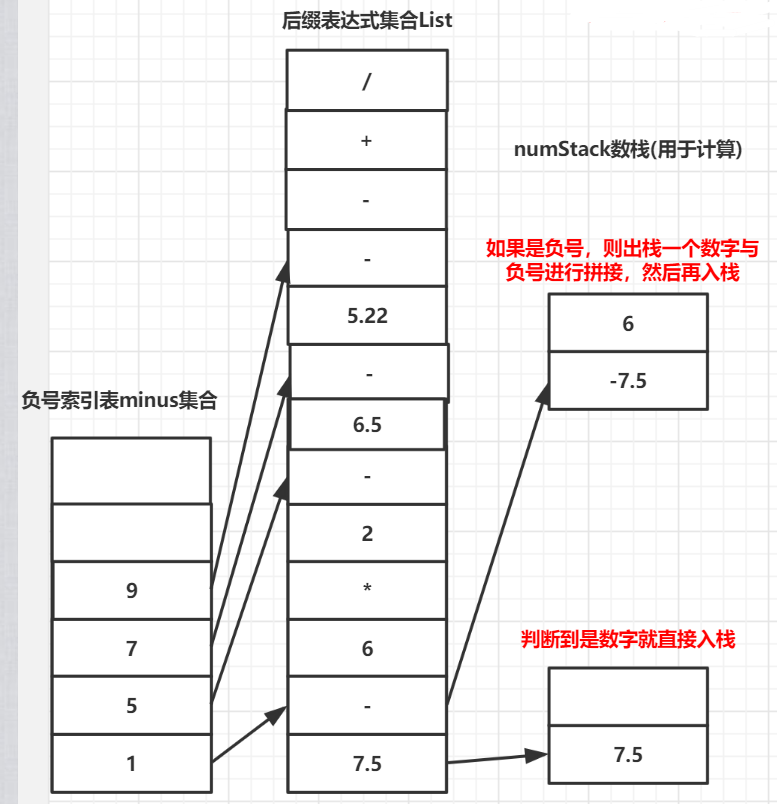
接下来处理运算符号：

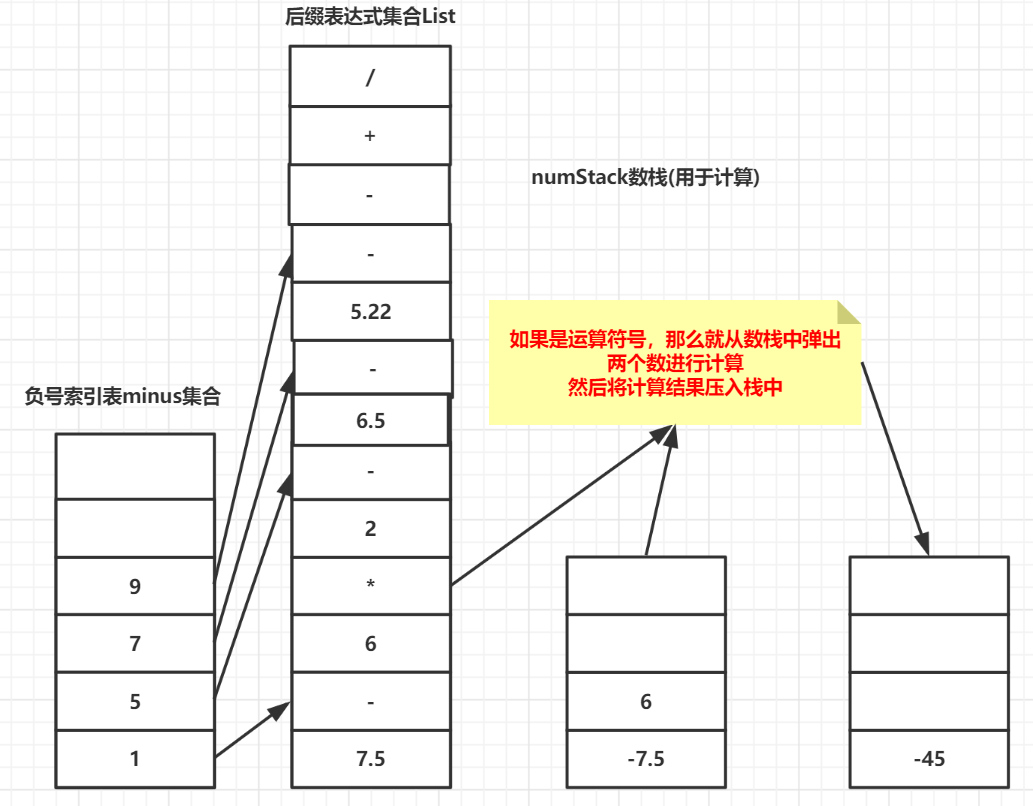
重复以上动作，直到后缀表达式List为空，即得：

---

后缀表达式计算代码：

---

// 后缀表达式list进行计算
    public double calcRPN(List<String> rPN) {
        Stack<Double> numStack=new Stack<Double>();
        boolean flag=false;//用来标记是否处理过负号
        for (int i=0; i < rPN.size(); i++) {
            if (isOper( rPN.get( i ) )) {
                if (rPN.get( i ).equals( "-" )) {//这里判断两次，是为了提高查找负号索引位置的效率
                    for (int j=0; j < minus.size(); j++) {//遍历后缀表达式集合中记录的负号的索引下标
                        if (i == minus.get( j )) {//如果rPN后缀表达式的下标等于minus集合中记录的负号索引下标
                            String min=rPN.get( i );//说明此位置的‘-’号，为负号而不是减号
                            Double num=numStack.pop();//那么就pop出数栈，和-拼接
                            numStack.push( Double.parseDouble( min + num ) );
                            flag=true;
                            continue;
                        }
                    }
                    if (flag) {
                        flag=false;
                        continue;
                    }
                }//下面就是常规计算,一定要思量上面两个continue的作用
                double num1=numStack.pop();
                double num2=numStack.pop();
                numStack.push( calc( num1, num2, rPN.get( i ).charAt( 0 ) ) );
            } else {//如果是数字就直接丢到数栈
                numStack.push( Double.valueOf( rPN.get( i ) ) );
            }
        }
        return numStack.pop();
    }

接下来是完成源代码：

---

public class ReversePolishNotationCalcDemo {
    List<Integer> minus;//用于记录符号出现的索引

    public static void main(String[] args) {
        String expression="-7.5*6/(-2+(-6.5- -5.22))";// 7.5 - 6.5 5.22 - - *
        expression="7.5+-3*8/(7+2)";
        ReversePolishNotationCalcDemo rpn=new ReversePolishNotationCalcDemo();
        System.out.print( "中缀表达式为：" );

        rpn.getList( expression ).forEach( System.out::print );

//        for (String s : rpn.getList(expression)) {
//            System.out.printf("%s  ", s);
//        }
        System.out.println();
        System.out.print( "后缀表达式为：" );
        for (String s : rpn.toRPN( expression )) {
            System.out.printf( "%s  ", s );
        }
        System.out.println();
        double result=rpn.calcRPN( rpn.toRPN( expression ) );
        System.out.println( expression.replace( " ", "" ) + " = " + result );
    }

    // 后缀表达式list进行计算
    public double calcRPN(List<String> rPN) {
        Stack<Double> numStack=new Stack<Double>();
        boolean flag=false;
        for (int i=0; i < rPN.size(); i++) {
            if (isOper( rPN.get( i ) )) {
                if (rPN.get( i ).equals( "-" )) {
                    for (int j=0; j < minus.size(); j++) {
                        if (i == minus.get( j )) {
                            String min=rPN.get( i );
                            Double num=numStack.pop();
                            numStack.push( Double.parseDouble( min + num ) );
                            flag=true;
                            continue;
                        }
                    }
                    if (flag) {
                        flag=false;
                        continue;
                    }
                }
                double num1=numStack.pop();
                double num2=numStack.pop();
                numStack.push( calc( num1, num2, rPN.get( i ).charAt( 0 ) ) );
            } else {
                numStack.push( Double.valueOf( rPN.get( i ) ) );
            }
        }
        return numStack.pop();
    }

    // 中缀表达式转后缀表达式
    public List<String> toRPN(String expression) {
        List<String> list=getList( expression );
        List<String> rPN=new ArrayList<String>();// 用于存放后缀表达式
        Stack<String> exp=new Stack<String>();// 用于操作判断符号
        minus=new ArrayList<>();
        for (String s : list) {// 将中缀表达式每个元素list遍历
            if (isOper( s )) {// 如果字符串是+-*/
                if (exp.isEmpty())// 如果栈是空，那么就直接入栈
                    exp.push( s );//-7.5*6/(-2+(-6.5- -5.22))
                else if (priority( s ) <= priority( exp.peek() )) {// 如果栈里面有运算符，那么就和栈顶运算符比较优先级
                    rPN.add( exp.pop() );// 当前运算符优先级小于栈顶运算符，就把栈顶运算符弹出加入到后缀表达式rPN列表中
                    exp.push( s );// 然后压入当前运算符
                } else
                    exp.push( s );

            } else if (s.equals( ")" )) {// 如果当前字符串是‘)’那么就将栈顶字符串加入add到List rPN中，直到栈顶字符串为"("
                while (!exp.peek().equals( "(" )) {
                    rPN.add( exp.pop() );
                }
                exp.pop();// 一定要记得将左括号(弹出去，代表一对小括号完成计算
            } else if (s.equals( "(" ))
                exp.push( s );// 如果是左括号就直接入栈
            else {// 否则就是数字，直接加入rPN中
                if (s.charAt( 0 ) == '-') {
                    rPN.add( s.substring( 1, s.length() ) );
                    rPN.add( "" + s.charAt( 0 ) );
                    minus.add( rPN.size() - 1 );
                } else
                    rPN.add( s );
            }
        }
        while (!exp.isEmpty()) {// 最后扫描完list后，将栈exp中的字符串依次加入到rPN后缀表达式列表中
            rPN.add( exp.pop() );
        }
        System.out.println( "负号出现的索引:" + Arrays.toString( minus.toArray() ) );
        return rPN;
    }

    // 表达式转中缀表达式(支持小数点，负数，小括号)
    public List<String> getList(String expression) {
        List<String> exp=new ArrayList<String>();
        String merge="";
        int index=0;
        char ch, ch1=0;
        boolean flag=false;
        expression=expression.replace( " ", "" );
        while (index != expression.length()) {
            ch=expression.substring( index, index + 1 ).charAt( 0 );
            merge+=ch;
            if (index < expression.length() - 1) {// 防止下标越界
                ch1=expression.substring( index + 1, index + 2 ).charAt( 0 );
                if (isOper( ch1 )) {
                    exp.add( merge );
                    merge="";
                    flag=false;
                } else if (isOper( ch )) {
                    if (flag == false && exp.size() > 0) {//-7.5*6/(-2+(-6.5- -5.22))
                        exp.add( merge );
                        merge="";
                        flag=false;
                    }
                }
                if (ch == '(' && ch1 == '-' || isOper( ch ) && ch1 == '-')
                    flag=true;
            }
            index++;
        }
        exp.add( merge );
        return exp;
    }

    public boolean isOper(String oper) {
        return oper.equals( "+" ) || oper.equals( "-" ) || oper.equals( "*" ) || oper.equals( "/" );
    }

    public boolean isOper(char oper) {
        return oper == '+' || oper == '-' || oper == '*' || oper == '/' || oper == '(' || oper == ')';
    }

    public int priority(String s) {
        if (s.equals( "+" ) || s.equals( "-" ))
            return 0;
        if (s.equals( "*" ) || s.equals( "/" ))
            return 1;
        return -1;
    }

    public double calc(double num1, double num2, int oper) {
        switch (oper) {
            case '+':
                return num1 + num2;
            case '-':
                return num2 - num1;
            case '*':
                return num1 * num2;
            case '/':
                return num2 / num1;
            default:
                break;
        }
        return 0;
    }
}

完整源代码