JavaScript实现树结构(二)
JavaScript实现树结构(二)
一、二叉搜索树的封装
二叉树搜索树的基本属性:
如图所示:二叉搜索树有四个最基本的属性:指向节点的根(root),节点中的键(key)、左指针(right)、右指针(right)。
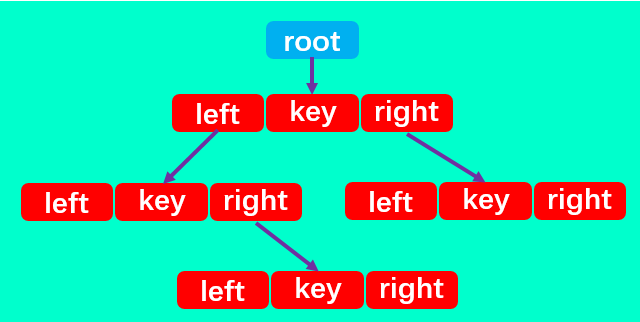
所以,二叉搜索树中除了定义root属性外,还应定义一个节点内部类,里面包含每个节点中的left、right和key三个属性:
//封装二叉搜索树
function BinarySearchTree(){
//节点内部类
function Node(key){
this.key = key
this.left = null
this.right = null
}
//属性
this.root = null
}
二叉搜索树的常见操作:
- insert(key):向树中插入一个新的键;
- search(key):在树中查找一个键,如果节点存在,则返回true;如果不存在,则返回false;
- inOrderTraverse:通过中序遍历方式遍历所有节点;
- preOrderTraverse:通过先序遍历方式遍历所有节点;
- postOrderTraverse:通过后序遍历方式遍历所有节点;
- min:返回树中最小的值/键;
- max:返回树中最大的值/键;
- remove(key):从树中移除某个键;
1.插入数据
实现思路:
- 首先根据传入的key创建节点对象;
- 然后判断根节点是否存在,不存在时通过:this.root = newNode,直接把新节点作为二叉搜索树的根节点。
- 若存在根节点则重新定义一个内部方法insertNode()用于查找插入点。
//insert方法:对外向用户暴露的方法
BinarySearchTree.prototype.insert = function(key){
//1.根据key创建节点
let newNode = new Node(key)
//2.判断根节点是否存在
if (this.root == null) {
this.root = newNode
//根节点存在时
}else {
this.insertNode(this.root, newNode)
}
}
内部方法insertNode()的实现思路:
根据比较传入的两个节点,一直查找新节点适合插入的位置,直到成功插入新节点为止。
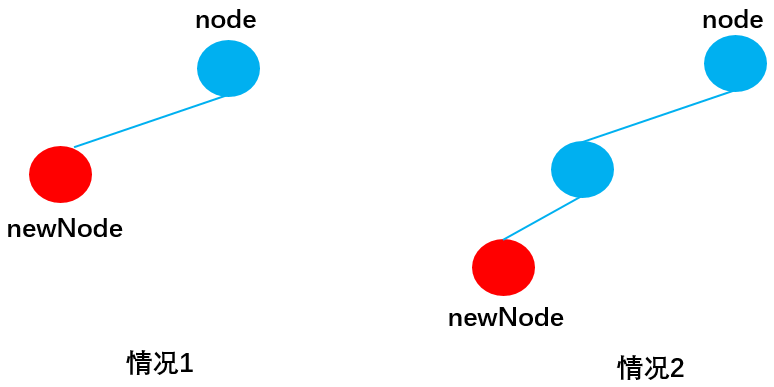
当newNode.key < node.key向左查找:
情况1:当node无左子节点时,直接插入:
情况2:当node有左子节点时,递归调用insertNode(),直到遇到无左子节点成功插入newNode后,不再符合该情况,也就不再调用insertNode(),递归停止。
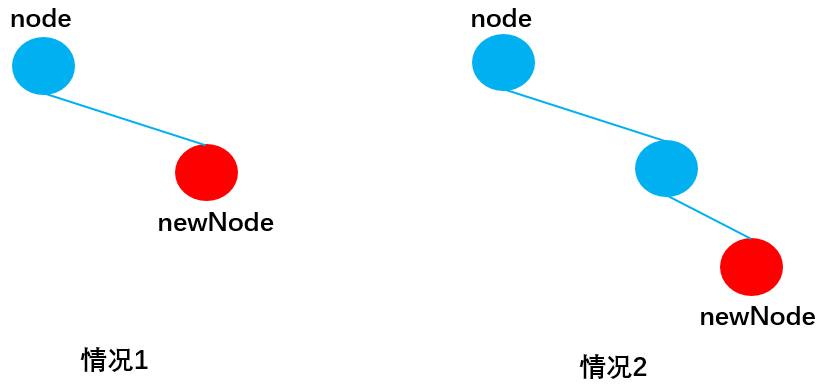
当newNode.key >= node.key向右查找,与向左查找类似:
情况1:当node无右子节点时,直接插入:
情况2:当node有右子节点时,依然递归调用insertNode(),直到遇到传入insertNode方法的node无右子节点成功插入newNode为止:
insertNode()代码实现:
//内部使用的insertNode方法:用于比较节点从左边插入还是右边插入
BinarySearchTree.prototype.insertNode = function(node, newNode){
//当newNode.key < node.key向左查找
/*----------------------分支1:向左查找--------------------------*/
if(newNode.key < node.key){
//情况1:node无左子节点,直接插入
/*----------------------分支1.1--------------------------*/
if (node.left == null) {
node.left = newNode
//情况2:node有左子节点,递归调用insertNode(),直到遇到无左子节点成功插入newNode后,不再符合该情况,也就不再调用insertNode(),递归停止。
/*----------------------分支1.2--------------------------*/
}else{
this.insertNode(node.left, newNode)
}
//当newNode.key >= node.key向右查找
/*-----------------------分支2:向右查找--------------------------*/
}else{
//情况1:node无右子节点,直接插入
/*-----------------------分支2.1--------------------------*/
if(node.right == null){
node.right == newNode
//情况2:node有右子节点,依然递归调用insertNode(),直到遇到无右子节点成功插入newNode为止
/*-----------------------分支2.2--------------------------*/
}else{
this.insertNode(node.right, newNode)
}
}
}
过程详解:
为了更好理解以下列二叉搜索树为例:
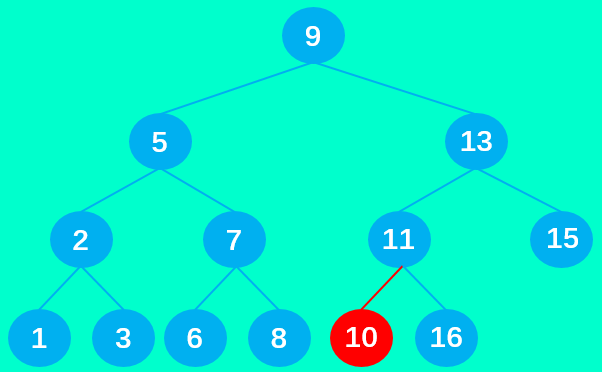
想要上述的二叉搜索树(蓝色)中插入数据10:
- 先把key = 10 传入insert方法,由于存在根节点 9,所以直接调用insetNode方法,传入的参数:node = 9,newNode = 10;
- 由于10 > 9,进入分支2,向右查找适合插入的位置;
- 由于根节点 9 的右子节点存在且为 13 ,所以进入分支2.2,递归调用insertNode方法,传入的参数:node = 13,newNode = 10;
- 由于 10 < 13 ,进入分支1,向左查找适合插入的位置;
- 由于父节点 13 的左子节点存在且为11,所以进入分支1.2,递归调用insertNode方法,传入的参数:node = 11,newNode = 10;
- 由于 10 < 11,进入分支1,向左查找适合插入的位置;
- 由于父节点 11 的左子节点不存在,所以进入分支1.1,成功插入节点 10 。由于不符合分支1.2的条件所以不会继续调用insertNode方法,递归停止。
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(9);
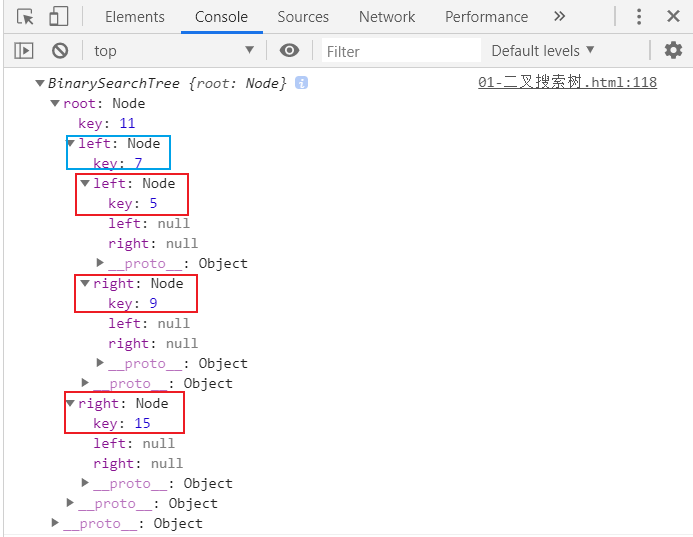
console.log(bst);
应得到下图所示的二叉搜索树:
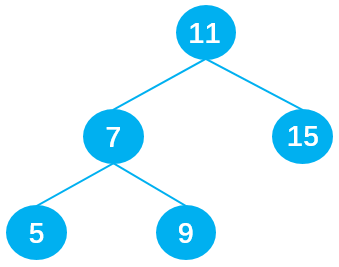
测试结果
2.遍历数据
这里所说的树的遍历不仅仅针对二叉搜索树,而是适用于所有的二叉树。由于树结构不是线性结构,所以遍历方式有多种选择,常见的三种二叉树遍历方式为:
- 先序遍历;
- 中序遍历;
- 后序遍历;
还有层序遍历,使用较少。
2.1.先序遍历
先序遍历的过程为:
- 首先,遍历根节点;
- 然后,遍历其左子树;
- 最后,遍历其右子树;
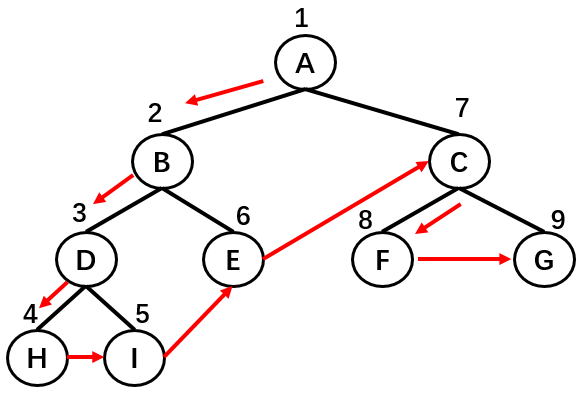
如上图所示,二叉树的节点遍历顺序为:A -> B -> D -> H -> I -> E -> C -> F -> G。
代码实现:
//先序遍历
//掺入一个handler函数方便之后对得到的key进行处理
BinarySearchTree.prototype.preOrderTraversal = function(handler){
this.preOrderTraversalNode(this.root, handler)
}
//封装内部方法,对某个节点进行遍历
BinarySearchTree.prototype.preOrderTraversalNode = function(node,handler){
if (node != null) {
//1.处理经过的节点
handler(node.key)
/*----------------------递归1----------------------------*/
//2.遍历左子树中的节点
this.preOrderTraversalNode(node.left, handler)
/*----------------------递归2----------------------------*/
//3.遍历右子树中的节点
this.preOrderTraversalNode(node.right, handler)
}
}
过程详解:
以遍历以下二叉搜索树为例:
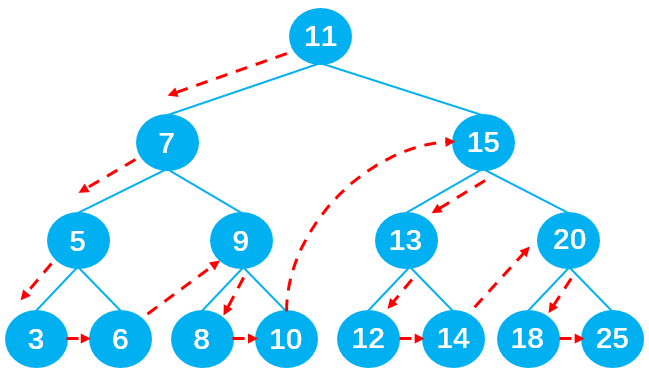
首先调用preOrderTraversal方法,在方法里再调用preOrderTraversalNode方法用于遍历二叉搜索树。在preOrderTraversalNode方法中,递归1负责遍历左子节点,递归2负责遍历右子节点。先执行递归1,执行过程如下图所示:
记:preOrderTraversalNode() 为 A()
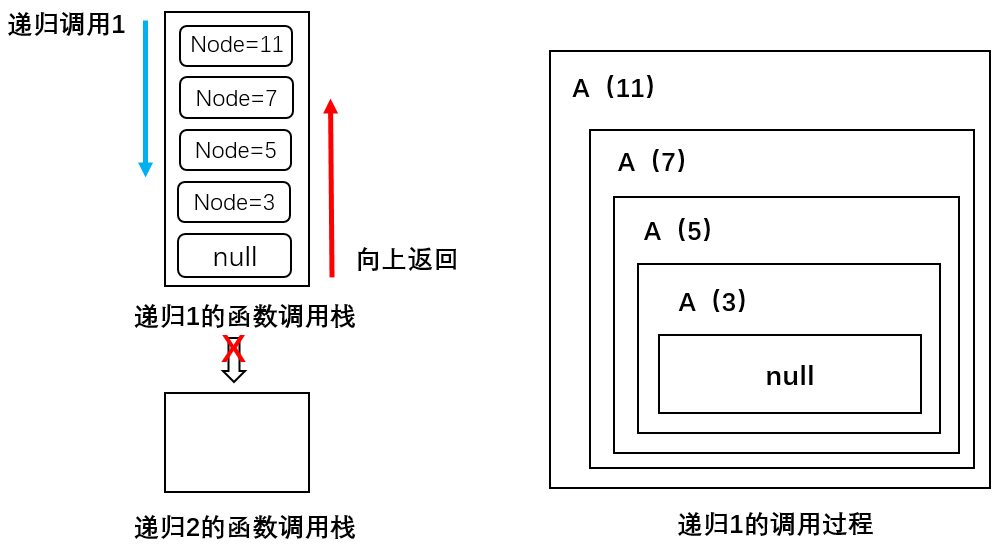
可以看到一共递归调用了4次方法A,分别传入11、7、5、3,最后遇到null不满足 node != null 条件结束递归1;注意此时只是执行完最开始的递归1,并没有执行递归2,并且递归1执行到null停止后要一层层地往上返回,按顺序将调用的函数压出函数调用栈。
关于函数调用栈:之前的四次递归共把4个函数压入了函数调用栈,现在递归执行完了一层层地把函数压出栈。
值得注意的是:每一层函数都只是执行完了递归1,当返回到该层函数时,比如A(3)要继续执行递归2遍历二叉搜索树中的右子节点;
在执行递归2的过程中会不断调用方法A,并依次执行递归1和递归2,以此类推直到遇到null不满足 node != null 条件为止,才停止递归并一层层返回,如此循环。同理A(5)层、A(7)层、A(11)层都要经历上述循环,直到将二叉搜索树中的节点全部遍历完为止。
具体过程如下图所示:

测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
//3.测试遍历
let resultString = ""
//掺入处理节点值的处理函数
bst.preOrderTraversal(function(key){
resultString += key + "->"
})
alert(resultString)
应输出这样的顺序:11 -> 7 -> 5 -> 3 -> 6 -> 9 -> 8 -> 10 -> 15 -> 13 ->12 -> 14 -> 20 -> 18 -> 25 。
测试结果:

2.2.中序遍历
实现思路:与先序遍历原理相同,只不过是遍历的顺序不一样了。
- 首先,遍历其左子树;
- 然后,遍历根(父)节点;
- 最后,遍历其右子树;
代码实现:
//中序遍历
BinarySearchTree.prototype.midOrderTraversal = function(handler){
this.midOrderTraversalNode(this.root, handler)
}
BinarySearchTree.prototype.midOrderTraversalNode = function(node, handler){
if (node != null) {
//1.遍历左子树中的节点
this.midOrderTraversalNode(node.left, handler)
//2.处理节点
handler(node.key)
//3.遍历右子树中的节点
this.midOrderTraversalNode(node.right, handler)
}
}
过程详解:
遍历的顺序应如下图所示:

首先调用midOrderTraversal方法,在方法里再调用midOrderTraversalNode方法用于遍历二叉搜索树。先使用递归1遍历左子树中的节点;然后,处理父节点;最后,遍历右子树中的节点。
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
//3.测试中序遍历
let resultString2 =""
bst.midOrderTraversal(function(key){
resultString2 += key + "->"
})
alert(resultString2)
输出节点的顺序应为:3 -> 5 -> 6 -> 7 -> 8 -> 9 -> 10 -> 11 -> 12 -> 13 -> 14 -> 15 -> 18 -> 20 -> 25 。
测试结果:

2.3.后续遍历
实现思路:与先序遍历原理相同,只不过是遍历的顺序不一样了。
- 首先,遍历其左子树;
- 然后,遍历其右子树;
- 最后,遍历根(父)节点;
代码实现:
//后序遍历
BinarySearchTree.prototype.postOrderTraversal = function(handler){
this.postOrderTraversalNode(this.root, handler)
}
BinarySearchTree.prototype.postOrderTraversalNode = function(node, handler){
if (node != null) {
//1.遍历左子树中的节点
this.postOrderTraversalNode(node.left, handler)
//2.遍历右子树中的节点
this.postOrderTraversalNode(node.right, handler)
//3.处理节点
handler(node.key)
}
}
过程详解:
遍历的顺序应如下图所示:

首先调用postOrderTraversal方法,在方法里再调用postOrderTraversalNode方法用于遍历二叉搜索树。先使用递归1遍历左子树中的节点;然后,遍历右子树中的节点;最后,处理父节点。
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
//3.测试后序遍历
let resultString3 =""
bst.postOrderTraversal(function(key){
resultString3 += key + "->"
})
alert(resultString3)
输出节点的顺序应为:3 -> 6 -> 5 -> 8 -> 10 -> 9 -> 7 -> 12 -> 14 -> 13 -> 18 -> 25 -> 20 -> 15 -> 11 。
测试结果:

总结:以遍历根(父)节点的顺序来区分三种遍历方式。比如:先序遍历先遍历根节点、中序遍历第二遍历根节点、后续遍历最后遍历根节点。
3.查找数据
3.1.查找最大值&最小值
在二叉搜索树中查找最值非常简单,最小值在二叉搜索树的最左边,最大值在二叉搜索树的最右边。只需要一直向左/右查找就能得到最值,如下图所示:

代码实现:
//寻找最大值
BinarySearchTree.prototype.max = function () {
//1.获取根节点
let node = this.root
//2.定义key保存节点值
let key = null
//3.依次向右不断查找,直到节点为null
while (node != null) {
key = node.key
node = node.right
}
return key
}
//寻找最小值
BinarySearchTree.prototype.min = function(){
//1.获取根节点
let node = this.root
//2.定义key保存节点值
let key = null
//3.依次向左不断查找,直到节点为null
while (node != null) {
key = node.key
node = node.left
}
return key
}
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
//4.测试最值
console.log(bst.max());
console.log(bst.min());
测试结果:

3.2.查找特定值
查找二叉搜索树当中的特定值效率也非常高。只需要从根节点开始将需要查找节点的key值与之比较,若node.key < root则向左查找,若node.key > root就向右查找,直到找到或查找到null为止。这里可以使用递归实现,也可以采用循环来实现。
实现代码:
//查找特定的key
BinarySearchTree.prototype.search = function(key){
//1.获取根节点
let node = this.root
//2.循环搜索key
while(node != null){
if (key < node.key) {
//小于根(父)节点就往左边找
node = node.left
//大于根(父)节点就往右边找
}else if(key > node.key){
node = node.right
}else{
return true
}
}
return false
}
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
//3.测试搜索方法
console.log(bst.search(24));//false
console.log(bst.search(13));//true
console.log(bst.search(2));//false
测试结果:

4.删除数据
实现思路:
第一步:先找到需要删除的节点,若没找到,则不需要删除;
首先定义变量current用于保存需要删除的节点、变量parent用于保存它的父节点、变量isLeftChild保存current是否为parent的左节点,这样方便之后删除节点时改变相关节点的指向。
实现代码:
//1.1.定义变量
let current = this.root
let parent = null
let isLeftChild = true
//1.2.开始寻找删除的节点
while (current.key != key) {
parent = current
// 小于则往左查找
if (key < current.key) {
isLeftChild = true
current = current.left
} else{
isLeftChild = false
current = current.rigth
}
//找到最后依然没有找到相等的节点
if (current == null) {
return false
}
}
//结束while循环后:current.key = key
第二步:删除找到的指定节点,后分3种情况:
- 删除叶子节点;
- 删除只有一个子节点的节点;
- 删除有两个子节点的节点;
4.1.情况1:没有子节点
没有子节点时也有两种情况:
当该叶子节点为根节点时,如下图所示,此时current == this.root,直接通过:this.root = null,删除根节点。
当该叶子节点不为根节点时也有两种情况,如下图所示:

若current = 8,可以通过:parent.left = null,删除节点8;
若current = 10,可以通过:parent.right = null,删除节点10;
代码实现:
//情况1:删除的是叶子节点(没有子节点)
if (current.left == null && current.right ==null) {
if (current == this.root) {
this.root = null
}else if(isLeftChild){
parent.left = null
}else {
parent.right =null
}
}
4.2.情况2:有一个子节点
有六种情况分别是:
当current存在左子节点时(current.right == null):
情况1:current为根节点(current == this.root),如节点11,此时通过:this.root = current.left,删除根节点11;
情况2:current为父节点parent的左子节点(isLeftChild == true),如节点5,此时通过:parent.left = current.left,删除节点5;
情况3:current为父节点parent的右子节点(isLeftChild == false),如节点9,此时通过:parent.right = current.left,删除节点9;

当current存在右子节点时(current.left = null):
情况4:current为根节点(current == this.root),如节点11,此时通过:this.root = current.right,删除根节点11。
情况5:current为父节点parent的左子节点(isLeftChild == true),如节点5,此时通过:parent.left = current.right,删除节点5;
情况6:current为父节点parent的右子节点(isLeftChild == false),如节点9,此时通过:parent.right = current.right,删除节点9;

实现代码:
//情况2:删除的节点有一个子节点
//当current存在左子节点时
else if(current.right == null){
if (current == this.root) {
this.root = current.left
} else if(isLeftChild) {
parent.left = current.left
} else{
parent.right = current.left
}
//当current存在右子节点时
} else if(current.left == null){
if (current == this.root) {
this.root = current.rigth
} else if(isLeftChild) {
parent.left = current.right
} else{
parent.right = current.right
}
}
4.3.情况3:有两个子节点
这种情况十分复杂,首先依据以下二叉搜索树,讨论这样的问题:

删除节点9
在保证删除节点9后原二叉树仍为二叉搜索树的前提下,有两种方式:
- 方式1:从节点9的左子树中选择一合适的节点替代节点9,可知节点8符合要求;
- 方式2:从节点9的右子树中选择一合适的节点替代节点9,可知节点10符合要求;

删除节点7
在保证删除节点7后原二叉树仍为二叉搜索树的前提下,也有两种方式:
- 方式1:从节点7的左子树中选择一合适的节点替代节点7,可知节点5符合要求;
- 方式2:从节点7的右子树中选择一合适的节点替代节点7,可知节点8符合要求;

删除节点15
在保证删除节点15后原树二叉树仍为二叉搜索树的前提下,同样有两种方式:
- 方式1:从节点15的左子树中选择一合适的节点替代节点15,可知节点14符合要求;
- 方式2:从节点15的右子树中选择一合适的节点替代节点15,可知节点18符合要求;

相信你已经发现其中的规律了!
规律总结:如果要删除的节点有两个子节点,甚至子节点还有子节点,这种情况下需要从要删除节点下面的子节点中找到一个合适的节点,来替换当前的节点。
若用current表示需要删除的节点,则合适的节点指的是:
- current左子树中比current小一点点的节点,即current左子树中的最大值;
- current右子树中比current大一点点的节点,即current右子树中的最小值;
前驱&后继
在二叉搜索树中,这两个特殊的节点有特殊的名字:
- 比current小一点点的节点,称为current节点的前驱。比如下图中的节点5就是节点7的前驱;
- 比current大一点点的节点,称为current节点的后继。比如下图中的节点8就是节点7的后继;

代码实现:
查找需要被删除的节点current的后继时,需要在current的右子树中查找最小值,即在current的右子树中一直向左遍历查找;
查找前驱时,则需要在current的左子树中查找最大值,即在current的左子树中一直向右遍历查找。
下面只讨论查找current后继的情况,查找前驱的原理相同,这里暂不讨论。
4.4.完整实现
//删除节点
BinarySearchTree.prototype.remove = function(key){
/*------------------------------1.寻找要删除的节点---------------------------------*/
//1.1.定义变量current保存删除的节点,parent保存它的父节点。isLeftChild保存current是否为parent的左节点
let current = this.root
let parent = null
let isLeftChild = true
//1.2.开始寻找删除的节点
while (current.key != key) {
parent = current
// 小于则往左查找
if (key < current.key) {
isLeftChild = true
current = current.left
} else{
isLeftChild = false
current = current.right
}
//找到最后依然没有找到相等的节点
if (current == null) {
return false
}
}
//结束while循环后:current.key = key
/*------------------------------2.根据对应情况删除节点------------------------------*/
//情况1:删除的是叶子节点(没有子节点)
if (current.left == null && current.right ==null) {
if (current == this.root) {
this.root = null
}else if(isLeftChild){
parent.left = null
}else {
parent.right =null
}
}
//情况2:删除的节点有一个子节点
//当current存在左子节点时
else if(current.right == null){
if (current == this.root) {
this.root = current.left
} else if(isLeftChild) {
parent.left = current.left
} else{
parent.right = current.left
}
//当current存在右子节点时
} else if(current.left == null){
if (current == this.root) {
this.root = current.right
} else if(isLeftChild) {
parent.left = current.right
} else{
parent.right = current.right
}
}
//情况3:删除的节点有两个子节点
else{
//1.获取后继节点
let successor = this.getSuccessor(current)
//2.判断是否根节点
if (current == this.root) {
this.root = successor
}else if (isLeftChild){
parent.left = successor
}else{
parent.right = successor
}
//3.将后继的左子节点改为被删除节点的左子节点
successor.left = current.left
}
}
//封装查找后继的方法
BinarySearchTree.prototype.getSuccessor = function(delNode){
//1.定义变量,保存找到的后继
let successor = delNode
let current = delNode.right
let successorParent = delNode
//2.循环查找current的右子树节点
while(current != null){
successorParent = successor
successor = current
current = current.left
}
//3.判断寻找到的后继节点是否直接就是删除节点的right节点
if(successor != delNode.right){
successorParent.left = successor.right
successor.right = delNode.right
}
return successor
}
测试代码:
//测试代码
//1.创建BinarySearchTree
let bst = new BinarySearchTree()
//2.插入数据
bst.insert(11);
bst.insert(7);
bst.insert(15);
bst.insert(5);
bst.insert(3);
bst.insert(9);
bst.insert(8);
bst.insert(10);
bst.insert(13);
bst.insert(12);
bst.insert(14);
bst.insert(20);
bst.insert(18);
bst.insert(25);
bst.insert(6);
bst.insert(19);
//3.测试删除代码
//删除没有子节点的节点
bst.remove(3)
bst.remove(8)
bst.remove(10)
//删除有一个子节点的节点
bst.remove(5)
bst.remove(19)
//删除有两个子节点的节点
bst.remove(9)
bst.remove(7)
bst.remove(15)
//遍历二叉搜索树并输出
let resultString = ""
bst.midOrderTraversal(function(key){
resultString += key + "->"
})
alert(resultString)
测试结果:

可见三种情况的节点都被成功删除了。
5.二叉搜索树完整封装
//封装二叉搜索树
function BinarySearchTree(){
//节点内部类
function Node(key){
this.key = key
this.left = null
this.right = null
}
//属性
this.root = null
//方法
//一.插入数据:insert方法:对外向用户暴露的方法
BinarySearchTree.prototype.insert = function(key){
//1.根据key创建节点
let newNode = new Node(key)
//2.判断根节点是否存在
if (this.root == null) {
this.root = newNode
//根节点存在时
}else {
this.insertNode(this.root, newNode)
}
}
//内部使用的insertNode方法:用于比较节点从左边插入还是右边插入
BinarySearchTree.prototype.insertNode = function(node, newNode){
//当newNode.key < node.key向左查找
if(newNode.key < node.key){
//情况1:node无左子节点,直接插入
if (node.left == null) {
node.left = newNode
//情况2:node有左子节点,递归调用insertNode(),直到遇到无左子节点成功插入newNode后,不再符合该情况,也就不再调用insertNode(),递归停止。
}else{
this.insertNode(node.left, newNode)
}
//当newNode.key >= node.key向右查找
}else{
//情况1:node无右子节点,直接插入
if(node.right == null){
node.right = newNode
//情况2:node有右子节点,依然递归调用insertNode(),直到遇到无右子节点成功插入newNode为止
}else{
this.insertNode(node.right, newNode)
}
}
}
//二.树的遍历
//1.先序遍历
//掺入一个handler函数对得到的key进行处理
BinarySearchTree.prototype.preOrderTraversal = function(handler){
this.preOrderTraversalNode(this.root, handler)
}
//封装内部方法,对某个节点进行遍历
BinarySearchTree.prototype.preOrderTraversalNode = function(node,handler){
if (node != null) {
//1.处理经过的节点
handler(node.key)
//2.遍历经过节点的左子节点
this.preOrderTraversalNode(node.left, handler)
//3.遍历经过节点的右子节点
this.preOrderTraversalNode(node.right, handler)
}
}
//2.中序遍历
BinarySearchTree.prototype.midOrderTraversal = function(handler){
this.midOrderTraversalNode(this.root, handler)
}
BinarySearchTree.prototype.midOrderTraversalNode = function(node, handler){
if (node != null) {
//1.遍历左子树中的节点
this.midOrderTraversalNode(node.left, handler)
//2.处理节点
handler(node.key)
//3.遍历右子树中的节点
this.midOrderTraversalNode(node.right, handler)
}
}
//3.后序遍历
BinarySearchTree.prototype.postOrderTraversal = function(handler){
this.postOrderTraversalNode(this.root, handler)
}
BinarySearchTree.prototype.postOrderTraversalNode = function(node, handler){
if (node != null) {
//1.遍历左子树中的节点
this.postOrderTraversalNode(node.left, handler)
//2.遍历右子树中的节点
this.postOrderTraversalNode(node.right, handler)
//3.处理节点
handler(node.key)
}
}
//三.寻找最值
//寻找最大值
BinarySearchTree.prototype.max = function () {
//1.获取根节点
let node = this.root
//2.定义key保存节点值
let key = null
//3.依次向右不断查找,直到节点为null
while (node != null) {
key = node.key
node = node.right
}
return key
}
//寻找最小值
BinarySearchTree.prototype.min = function(){
//1.获取根节点
let node = this.root
//2.定义key保存节点值
let key = null
//3.依次向左不断查找,直到节点为null
while (node != null) {
key = node.key
node = node.left
}
return key
}
//查找特定的key
BinarySearchTree.prototype.search = function(key){
//1.获取根节点
let node = this.root
//2.循环搜索key
while(node != null){
if (key < node.key) {
//小于根(父)节点就往左边找
node = node.left
//大于根(父)节点就往右边找
}else if(key > node.key){
node = node.right
}else{
return true
}
}
return false
}
//四.删除节点
BinarySearchTree.prototype.remove = function(key){
/*------------------------------1.寻找要删除的节点---------------------------------*/
//1.1.定义变量current保存删除的节点,parent保存它的父节点。isLeftChild保存current是否为parent的左节点
let current = this.root
let parent = null
let isLeftChild = true
//1.2.开始寻找删除的节点
while (current.key != key) {
parent = current
// 小于则往左查找
if (key < current.key) {
isLeftChild = true
current = current.left
} else{
isLeftChild = false
current = current.right
}
//找到最后依然没有找到相等的节点
if (current == null) {
return false
}
}
//结束while循环后:current.key = key
/*------------------------------2.根据对应情况删除节点------------------------------*/
//情况1:删除的是叶子节点(没有子节点)
if (current.left == null && current.right ==null) {
if (current == this.root) {
this.root = null
}else if(isLeftChild){
parent.left = null
}else {
parent.right =null
}
}
//情况2:删除的节点有一个子节点
//当current存在左子节点时
else if(current.right == null){
if (current == this.root) {
this.root = current.left
} else if(isLeftChild) {
parent.left = current.left
} else{
parent.right = current.left
}
//当current存在右子节点时
} else if(current.left == null){
if (current == this.root) {
this.root = current.right
} else if(isLeftChild) {
parent.left = current.right
} else{
parent.right = current.right
}
}
//情况3:删除的节点有两个子节点
else{
//1.获取后继节点
let successor = this.getSuccessor(current)
//2.判断是否根节点
if (current == this.root) {
this.root = successor
}else if (isLeftChild){
parent.left = successor
}else{
parent.right = successor
}
//3.将后继的左子节点改为被删除节点的左子节点
successor.left = current.left
}
}
//封装查找后继的方法
BinarySearchTree.prototype.getSuccessor = function(delNode){
//1.定义变量,保存找到的后继
let successor = delNode
let current = delNode.right
let successorParent = delNode
//2.循环查找current的右子树节点
while(current != null){
successorParent = successor
successor = current
current = current.left
}
//3.判断寻找到的后继节点是否直接就是删除节点的right节点
if(successor != delNode.right){
successorParent.left = successor.right
successor.right = delNode.right
}
return successor
}
}
二、平衡树
二叉搜索树的缺陷:
当插入的数据是有序的数据,就会造成二叉搜索树的深度过大。比如原二叉搜索树右 11 7 15 组成,如下图所示:

当插入一组有序数据:6 5 4 3 2就会变成深度过大的搜索二叉树,会严重影响二叉搜索树的性能。

非平衡树
- 比较好的二叉搜索树,它的数据应该是左右均匀分布的;
- 但是插入连续数据后,二叉搜索树中的数据分布就变得不均匀了,我们称这种树为非平衡树;
- 对于一棵平衡二叉树来说,插入/查找等操作的效率是O(logN);
- 而对于一棵非平衡二叉树来说,相当于编写了一个链表,查找效率变成了O(N);
树的平衡性
为了能以较快的时间O(logN)来操作一棵树,我们需要保证树总是平衡的:
- 起码大部分是平衡的,此时的时间复杂度也是接近O(logN)的;
- 这就要求树中每个节点左边的子孙节点的个数,应该尽可能地等于右边的子孙节点的个数;
常见的平衡树
- AVL树:是最早的一种平衡树,它通过在每个节点多存储一个额外的数据来保持树的平衡。由于AVL树是平衡树,所以它的时间复杂度也是O(logN)。但是它的整体效率不如红黑树,开发中比较少用。
- 红黑树:同样通过一些特性来保持树的平衡,时间复杂度也是O(logN)。进行插入/删除等操作时,性能优于AVL树,所以平衡树的应用基本都是红黑树。
参考资料:JavaScript数据结构与算法
JavaScript实现树结构(二)的更多相关文章
- JavaScript实现树结构(一)
JavaScript实现树结构(一) 一.树结构简介 1.1.简单了解树结构 什么是树? 真实的树: 树的特点: 树一般都有一个根,连接着根的是树干: 树干会发生分叉,形成许多树枝,树枝会继续分化成更 ...
- JavaScript 入门教程二 在HTML中使用 JavaScript
一.使用 <script> 元素的方式有两种:直接在页面中嵌入 JavaScript 代码和引用外部 JavaScript 文件. 二.使用内嵌方式,一般写法为: <script t ...
- JavaScript基础笔记二
一.函数返回值1.什么是函数返回值 函数的执行结果2. 可以没有return // 没有return或者return后面为空则会返回undefined3.一个函数应该只返回一种类型的值 二.可变 ...
- JavaScript基本概念(二)
JavaScript 基本概念(二) 操作符和语句 目录 操作符 一元操作符 位操作符 布尔操作符 乘性操作符 其他操作符 语句部分 说起操作符,回忆下上一篇文章末尾说的话. 操作符 一元操作符 ++ ...
- 一些有用的javascript实例分析(二)
原文:一些有用的javascript实例分析(二) 5 求出数组中所有数字的和 window.onload = function () { var oBtn = document.getElement ...
- 如何对Javascript代码进行二次压缩(混淆)
如何对Javascript代码进行二次压缩(混淆) 对Javascript代码进行压缩(混淆),可以有效减少传输和加载时间.但是,不是所有的变量(方法)都能被混淆的,一般来说,只有非属性的变量(方法) ...
- 理解JavaScript继承(二)
理解JavaScript继承(二) 5.寄生式继承 function object(o) { function F() {} F.prototype = o; return new F(); } fu ...
- JavaScript学习记录二
title: JavaScript学习记录二 toc: true date: 2018-09-13 10:14:53 --<JavaScript高级程序设计(第2版)>学习笔记 要多查阅M ...
- 基础JavaScript练习(二)总结
任务目的 学习与实践JavaScript的基本语法.语言特性 练习使用JavaScript实现简单的排序算法 任务描述 基于上一任务 限制输入的数字在10-100 队列元素数量最多限制为60个,当超过 ...
随机推荐
- 68)PHP,cookie的详细属性和有效期
(1)cookie的有效期: 默认:会话周期结束(就是浏览器关闭),默认情况下,cookie会在浏览器关闭时失效,这种cookie是 临时cookie或者叫会话. 支持设置有效期,setcookie的 ...
- 限制IP每分钟访问10次
转载:https://www.jianshu.com/p/d1326ab657ff IP请求限制,之前用过redis的set设置时间戳一分钟过期:也用过nginx的IP限流配置.前者,没法解决“用户在 ...
- SQL语句简单应用(未完)
简介: SQL(structured query language)结构化查询语句,是一种数据库查询和程序设计语言,用于存取数据以及查询.更新和管理关系型数据库系统,同时也是数据库脚本文件的扩展名 ...
- 91)PHP,cookie代码展示
cookie练习的代码: (1)先设置:setcookie('key值‘,’value值’): (2)然后我执行那个文件, (3)获取我的cookie值,用$_cookie['key值’] cook ...
- libphp5.so可能遇到的问题(转摘)
libphp5.so可能遇到的问题(转摘) 安装完APACHE和PHP5后,经常在启动APACHE载入libphp5.so时发现问题.我把遇到的问题统计下来: 1.undefined symbol:S ...
- MOOC(4)- setup和teardown函数
import unittest class TestRequest(unittest.TestCase): @classmethod def setUpClass(cls): print(" ...
- iPhoneSE2要在印度独家生产真得没戏?
现在,关于iPhone SE2的消息层出不穷,总的来说,它是一款真实存在的手机,整体性能和iPhone5X/SE相似,大概可能差不多会加上一些"无线充电"之类的无聊功能.普通消费者 ...
- 吴裕雄--天生自然KITTEN编程:忍者追宝
- Java Random函数
Java中存在着两种Random函数: 1.java.lang.Math.Random: 调用这个Math.Random()函数能够返回带正号的double值,该值大于等于0.0且小于1.0,即取值范 ...
- MySQL5.7彻底取消主从复制
由于手误在master节点执行了stop slave;->change master to XXX;->start slave;的动作,后面虽然使用stop slave停止了主从复制,但是 ...
