降维处理PCA

要理解什么是降维，书上给出了一个很好但是有点抽象的例子。

说，看电视的时候屏幕上有成百上千万的像素点，那么其实每个画面都是一个上千万维度的数据；但是我们在观看的时候大脑自动把电视里面的场景放在我们所能理解的三维空间来理解，这个很自然的过程其实就是一个降维（dimensionallity reduction）的过程

 

降维有什么作用呢？

1. 数据在低维下更容易处理、更容易使用；
2. 相关特征，特别是重要特征更能在数据中明确的显示出来；如果只有两维或者三维的话，更便于可视化展示；
3. 去除数据噪声
4. 降低算法开销

 

常见的降维算法有主成分分析（principal component analysis,PCA）、因子分析（Factor Analysis）和独立成分分析（Independent Component Analysis，ICA），其中PCA是目前应用最为广泛的方法。

 

PCA原理

---

在PCA中，数据从原来的坐标系转换到新的坐标系，新坐标系的选择是由数据本身决定的。第一个坐标轴的选择是原始数据中方差最大的方向，从数据角度上来讲，这其实就是最重要的方向，即下图总直线B的方向。第二个坐标轴则是第一个的垂直或者说正交（orthogonal）方向，即下图中直线C的方向。该过程一直重复，重复的次数为原始数据中特征的数目。而这些方向所表示出的数据特征就被称为“主成分”。

 

那怎么来求出这些主成分呢？由线性代数的知识可以知道，通过数据集的协方差矩阵及其特征值分析，我们就可以求得这些主成分的值。一旦得到协方差矩阵的特征向量，就可以保留最大的N个值。然后可以通过把数据集乘上这N个特征向量转换到新的空间。

 

PCA实现

---

在python的numpy包中linalg模块的eig()方法可以用于求特征值和特征向量。

从上面的原理分析中我们可以得出讲数据转化成前N个主成分的伪代码如下：

1. 去除平均值
2. 计算协方差矩阵
3. 计算协方差矩阵的特征值和特征向量
4. 将特征值从大到小排序
5. 保留最上面的N个特征向量
6. 将数据转换到上述N个特征向量构建的新空间中

代码实现如下：

1. # 加载数据的函数
2. def loadData(filename, delim = '\t'):
3. fr = open(filename)
4. stringArr = [line.strip().split(delim) for line in fr.readlines()]
5. datArr = [map(float,line) for line in stringArr]
6. return mat(datArr)
8. # =================================
9. # 输入：dataMat：数据集
10. # topNfeat：可选参数，需要应用的N个特征，可以指定，不指定的话就会返回全部特征
11. # 输出：降维之后的数据和重构之后的数据
12. # =================================
13. def pca(dataMat, topNfeat=9999999):
14. meanVals = mean(dataMat, axis=0)# axis = 0表示计算纵轴
15. meanRemoved = dataMat - meanVals #remove mean
16. covMat = cov(meanRemoved, rowvar=0)# 计算协方差矩阵
17. eigVals,eigVects = linalg.eig(mat(covMat))# 计算特征值（eigenvalue）和特征向量
18. eigValInd = argsort(eigVals) #sort, sort goes smallest to largest
19. eigValInd = eigValInd[:-(topNfeat+1):-1] #cut off unwanted dimensions
20. redEigVects = eigVects[:,eigValInd] #reorganize eig vects largest to smallest
21. lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
22. reconMat = (lowDDataMat * redEigVects.T) + meanVals
23. return lowDDataMat, reconMat

在数据集上进行PCA操作：

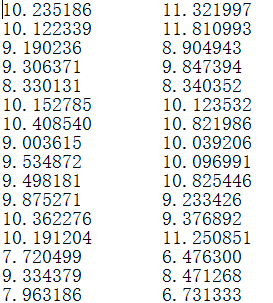
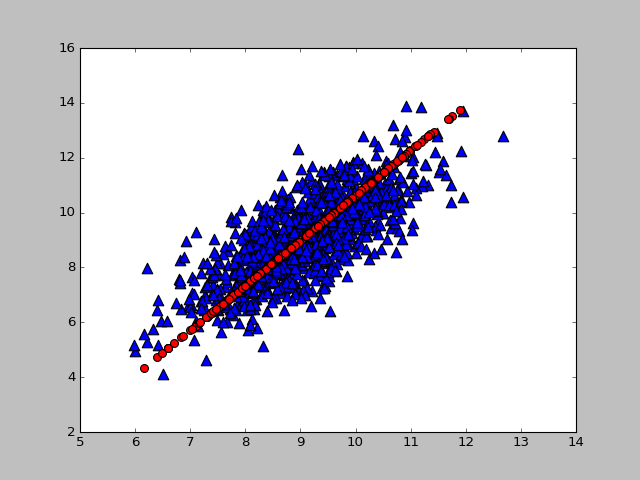
1. filename = r'E:\ml\machinelearninginaction\Ch13\testSet.txt'
2. dataMat = loadData(filename)
3. lowD, reconM = pca(dataMat, 1)

原始数据如下：

降维之后：

>>>shape(lowD)

得到（1000,1），可以看到两维降成了一维的数据

 

通过如下代码把降维后的数据和原始数据打印出来：

1. def plotData(dataMat,reconMat):
2. fig = plt.figure()
3. ax = fig.add_subplot(111)
4. # 绘制原始数据
5. ax.scatter(dataMat[:, 0].flatten().A[0], dataMat[:,1].flatten().A[0], marker='^', s = 90)
6. # 绘制重构后的数据
7. ax.scatter(reconMat[:,0].flatten().A[0], reconMat[:,1].flatten().A[0], marker='o', s = 10, c='red')
8. plt.show()

如下图所示：

降维之后的方向和我们之前讨论的最大方差方向是吻合的。

 

如果执行以下代码：

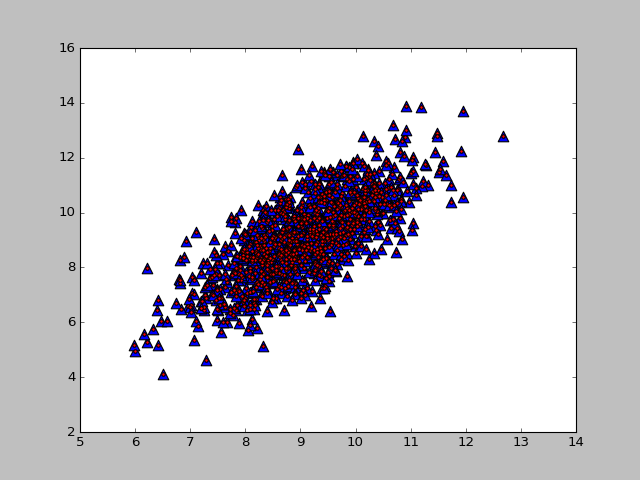
1. lowD, reconM = pca(dataMat, 2)

和原始数据的维度数一样，相当于没有降维，重构之后的数据会和原始数据重合，如下图所示：