【LeetCode】208. Implement Trie (Prefix Tree) 实现 Trie (前缀树)

作者： 负雪明烛
id： fuxuemingzhu
个人博客： http://fuxuemingzhu.cn/
公众号：负雪明烛
本文关键词：Leetcode, 力扣，Trie, 前缀树，字典树，208，Python, C++, Java

---

目录

• 题目描述
• 题目大意
• 解题方法
• • 从二叉树说起
  • 前缀树
  • • 构建
    • 查询
  • 应用
• 代码
• 刷题心得
• 日期

题目地址：https://leetcode.com/problems/implement-trie-prefix-tree/description/

题目描述

Implement a trie with insert, search, and startsWith methods.

Example:

Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // returns true
trie.search("app");     // returns false
trie.startsWith("app"); // returns true
trie.insert("app");
trie.search("app");     // returns true

Note:

1. You may assume that all inputs are consist of lowercase letters a-z.
2. All inputs are guaranteed to be non-empty strings.

题目大意

实现字典树。字典树：

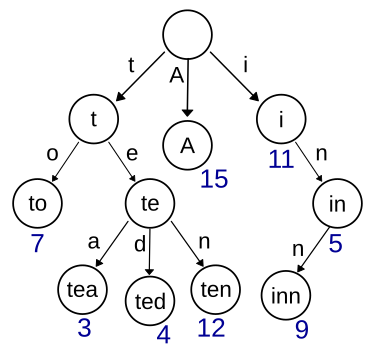
上图是一棵Trie树，表示一个保存了8个键的trie结构，“A”, “to”, “tea”, “ted”, “ten”, “i”, “in”, and “inn”.。

从上图可以归纳出Trie树的基本性质：

1. 根节点不包含字符，除根节点外的每一个子节点都包含一个字符。
2. 从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。
   每个节点的所有子节点包含的字符互不相同。
3. 通常在实现的时候，会在节点结构中设置一个标志，用来标记该结点处是否构成一个单词（关键字）。

可以看出，Trie树的关键字一般都是字符串，而且Trie树把每个关键字保存在一条路径上，而不是一个结点中。另外，两个有公共前缀的关键字，在Trie树中前缀部分的路径相同，所以Trie树又叫做前缀树（Prefix Tree）。

解题方法

本文写成前缀树入门教程。

从二叉树说起

前缀树，也是一种树。为了理解前缀树，我们先从二叉树说起。

常见的二叉树结构是下面这样的：

class TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;
}

可以看到一个树的节点包含了三个元素：该节点本身的值，左子树的指针，右子树的指针。二叉树可视化是下面这样的：

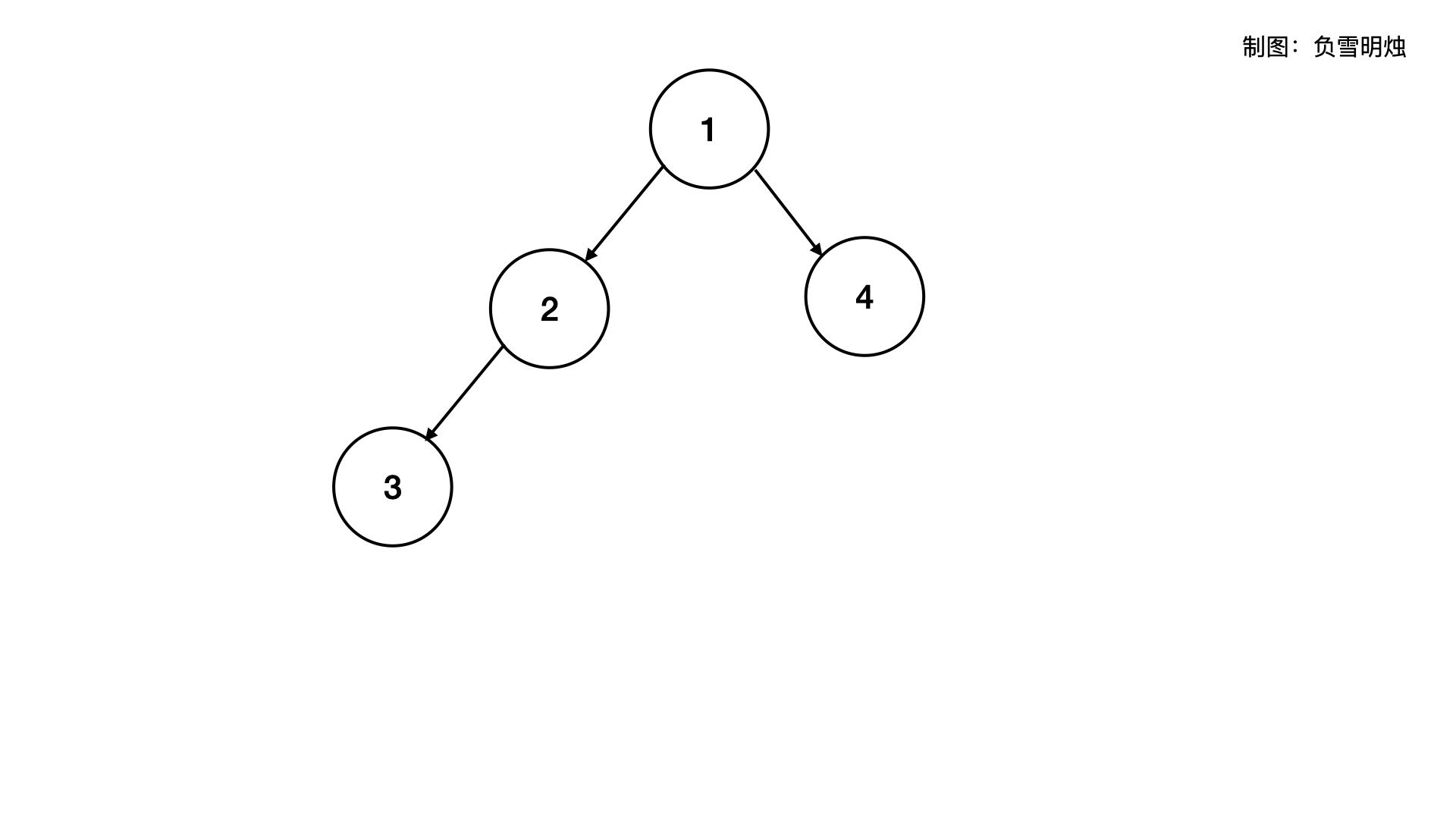
二叉树的每个节点只有两个孩子，那如果每个节点可以有多个孩子呢？这就形成了多叉树。多叉树的子节点数目一般不是固定的，所以会用变长数组来保存所有的子节点的指针。多叉树的结构是下面这样：

class TreeNode {
    int val;
    vector<TreeNode*> children;
}

多叉树可视化是下面这样：

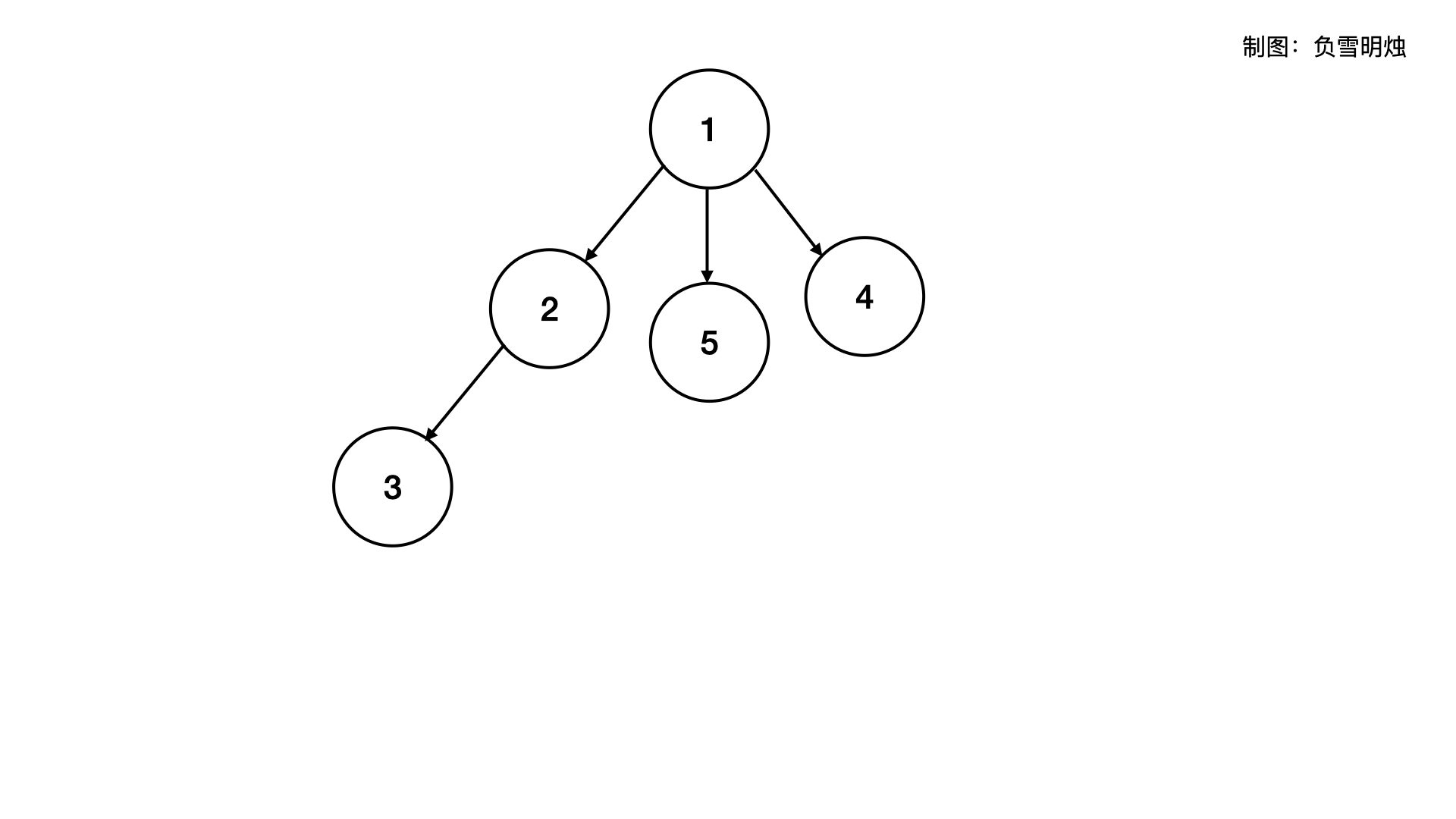
对于普通的多叉树，每个节点的所有子节点可能是没有任何规律的。而本题讨论的「前缀树」就是每个节点的 children 有规律的多叉树。

前缀树

（只保存小写字符的）「前缀树」是一种特殊的多叉树，它的 TrieNode 中 chidren 是一个大小为 26 的一维数组，分别对应了26个英文字符 'a' ~ 'z'，也就是说形成了一棵 26叉树。

前缀树的结构可以定义为下面这样。
里面存储了两个信息：

• isWord 表示从根节点到当前节点为止，该路径是否形成了一个有效的字符串。
• children 是该节点的所有子节点。

class TrieNode {
public:
    vector<TrieNode*> children;
    bool isWord;
    TrieNode() : isWord(false), children(26, nullptr) {
    }
    ~TrieNode() {
        for (auto& c : children)
            delete c;
    }
};

构建

在构建前缀树的时候，按照下面的方法：

• 根节点不保存任何信息；
• 关键词放到「前缀树」时，需要把它拆成各个字符，每个字符按照其在 'a' ~ 'z' 的序号，放在对应的 chidren 里面。下一个字符是当前字符的子节点。
• 一个输入字符串构建「前缀树」结束的时候，需要把该节点的 isWord 标记为 true，说明从根节点到当前节点的路径，构成了一个关键词。

下面是一棵「前缀树」，其中保存了 {"am", "an", "as", "b", "c", "cv"} 这些关键词。图中红色表示 isWord 为 true。
看下面这个图的时候需要注意：

1. 所有以相同字符开头的字符串，会聚合到同一个子树上。比如 {"am", "an", "as"} ；
2. 并不一定是到达叶子节点才形成了一个关键词，只要 isWord 为true，那么从根节点到当前节点的路径就是关键词。比如 {"c", "cv"} ；

有些题解把字符画在了节点中，我认为是不准确的。因为前缀树是根据 字符在 children 中的位置确定子树，而不真正在树中存储了 'a' ~ 'z' 这些字符。树中每个节点存储的 isWord，表示从根节点到当前节点的路径是否构成了一个关键词。

查询

在判断一个关键词是否在「前缀树」中时，需要依次遍历该关键词所有字符，在前缀树中找出这条路径。可能出现三种情况：

1. 在寻找路径的过程中，发现到某个位置路径断了。比如在上面的前缀树图中寻找 "d" 或者 "ar" 或者 "any" ，由于树中没有构建对应的节点，那么就查找不到这些关键词；
2. 找到了这条路径，但是最后一个节点的 isWord 为 false。这也说明没有改关键词。比如在上面的前缀树图中寻找 "a" ；
3. 找到了这条路径，并且最后一个节点的 isWord 为 true。这说明前缀树存储了这个关键词，比如上面前缀树图中的 "am" , "cv" 等。

应用

上面说了这么多前缀树，那前缀树有什么用呢？

• 比如我们常见的电话拨号键盘，当我们输入一些数字的时候，后面会自动提示以我们的输入数字为开头的所有号码。
• 比如我们的英文输入法，当我们输入半个单词的时候，输入法上面会自动联想和补全后面可能的单词。
• 再比如在搜索框搜索的时候，输入"负雪"，后面会联想到 负雪明烛 。

等等。

代码

下面的 Python 解法中，保存 children 是使用的字典，它保存的结构是 {字符：Node} ，所以可以直接通过 children[‘a’] 来获取当前节点的 ‘a’ 子树。

下面的 C++ 解法中，保存 children 用的题解分析时讲的大小为 26 的数组实现的。而且我的 C++ 解法中写出了很多人容易忽略的一个细节，就是 TrieNode 析构的时候，需要手动释放内存。

Python 代码如下：

class Node(object):
    def __init__(self):
        self.children = collections.defaultdict(Node)
        self.isword = False

class Trie(object):

    def __init__(self):
        self.root = Node()

    def insert(self, word):
        current = self.root
        for w in word:
            current = current.children[w]
        current.isword = True

    def search(self, word):
        current = self.root
        for w in word:
            current = current.children.get(w)
            if current == None:
                return False
        return current.isword

    def startsWith(self, prefix):
        current = self.root
        for w in prefix:
            current = current.children.get(w)
            if current == None:
                return False
        return True

C++ 代码如下：

class TrieNode {
public:
    vector<TrieNode*> children;
    bool isWord;
    TrieNode() : isWord(false), children(26, nullptr) {
    }
    ~TrieNode() {
        for (auto& c : children)
            delete c;
    }
};

class Trie {
public:
    /** Initialize your data structure here. */
    Trie() {
        root = new TrieNode();
    }

    /** Inserts a word into the trie. */
    void insert(string word) {
        TrieNode* p = root;
        for (char a : word) {
            int i = a - 'a';
            if (!p->children[i])
                p->children[i] = new TrieNode();
            p = p->children[i];
        }
        p->isWord = true;
    }

    /** Returns if the word is in the trie. */
    bool search(string word) {
        TrieNode* p = root;
        for (char a : word) {
            int i = a - 'a';
            if (!p->children[i])
                return false;
            p = p->children[i];
        }
        return p->isWord;
    }

    /** Returns if there is any word in the trie that starts with the given prefix. */
    bool startsWith(string prefix) {
        TrieNode* p = root;
        for (char a : prefix) {
            int i = a - 'a';
            if (!p->children[i])
                return false;
            p = p->children[i];
        }
        return true;
    }
private:
    TrieNode* root;
};

• 时间复杂度：

  O

  (

  字

  符

  串

  长

  度

  )

  O(字符串长度)

  O(字符串长度)，插入和查询操作需要遍历一次字符串。

• 空间复杂度：

  O

  (

  字

  符

  串

  长

  度

  之

  和

  )

  O(字符串长度之和)

  O(字符串长度之和)。

刷题心得

前缀树是挺有意思的应用。不过面试和力扣题目都考察不多，建议大家理解掌握，不必深究。

参考资料：

Trie树（Prefix Tree）介绍
力扣官方题解

---

OK，以上就是 @负雪明烛 写的今天题解的全部内容了，如果你觉得有帮助的话，求赞、求关注、求收藏。如果有疑问的话，请在下面评论，我会及时解答。

关注我，你将不会错过我的精彩动画题解、面试题分享、组队刷题活动，进入主页 @负雪明烛 右侧有刷题组织，从此刷题不再孤单。

祝大家 AC 多多，Offer 多多！我们明天再见！

日期

2018 年 2 月 27 日
2018 年 12 月 18 日 —— 改革开放40周年
2021 年 10 月 19 日