SAM 感性瞎扯

这里是 SAM 感性瞎扯。

最近学了后缀自动机（Suffix_Automaton，SAM），深感其巧妙之处，故写文以记之。

部分文字与图片来源于 OI-Wiki，hihoCoder 与一些个人博客，链接在文章最底端。

在此之前请先了解有关于 SAM 的所有函数，并最好理解 OI-Wiki 上有关于 SAM 的五条引理（链接在最底部，引理在下文中有提到）。

一些重要的定义与引理：

$T$：初始状态。
$\mathrm{endpos}(i)$：字符串 $i$ 在 $s$ 中所有出现的结束位置集合。例如当 $s=\texttt{"abcab"}$ 时，$\mathrm{endpos}(\texttt{"ab"})=\{2,5\}$，因为 $s[1:2]=s[4:5]=\texttt{"ab"}$。
$\mathrm{substr}(i)$：状态（SAM 上的一个节点）$i$ 所表示的所有子串的集合。
$\mathrm{shortest}(i)$：状态 $i$ 所表示的所有子串中，长度最短的那一个子串。
$\mathrm{longest}(i)$：状态 $i$ 所表示的所有子串中，长度最长的那一个子串。
$\mathrm{minlen}(i)$：状态 $i$ 所表示的所有子串中，长度最短的那一个子串的长度。即 $\mathrm{minlen}(i)=|\mathrm{shortest}(i)|$。
$\mathrm{len}(i)$：状态 $i$ 所表示的所有子串中，长度最长的那一个子串的长度。即 $\mathrm{len}(i)=|\mathrm{longest}(i)|$。
$\mathrm{link}(i)$：$\mathrm{longest}(i)$ 最长的一个后缀 $w\ (w\notin \mathrm{substr}(i))$ 所在的状态。换句话说，一个后缀链接 $\mathrm{link}(i)$ 连接到对应于 $\mathrm{longest}(i)$ 的最长后缀的另一个 $\mathrm{endpos}$ 等价类的状态。有 $\mathrm{minlen}(i)=\mathrm{len(link}(i))+1$。

引理 1：字符串 $s$ 的两个非空子串 $u$ 和 $w$（假设 $|u|\leq |w|$）的 $\mathrm{endpos}$ 相同，当且仅当字符串 $u$ 在 $s$ 中的每次出现，都以 $w$ 后缀的形式存在。证明详见 OI-Wiki，下（引理 2~5）同。

引理 2：考虑两个非空子串 $u$ 和 $w$（假设 $|u|\leq |w|$）。要么 $\mathrm{endpos}(u)\cup \mathrm{endpos}(w)=\varnothing$，要么 $\mathrm{endpos}(u)\subseteq\mathrm{endpos}(w)$，取决于 $u$ 是否为 $w$ 的一个后缀：

\[\begin{cases}\mathrm{endpos}(u)\subseteq\mathrm{endpos}(w)\quad &\mathrm{if}\ u\ \mathrm{is\ a\ suffix\ of}\ w\\\mathrm{endpos}(u)\cup \mathrm{endpos}(w)=\varnothing&\mathrm{otherwise}\end{cases}
\]

引理 3：考虑一个 $\mathrm{endpos}$ 等价类，将其中所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长，与此同时每个子串也是它前一个子串的后缀。换句话说，对于同一等价类的任一两子串，较短者总为为较长者的后缀，且该等价类中的子串长度恰好覆盖整个区间 $[\mathrm{minlen,len}]$（即排序后长度连续且不等）。

引理 4：所有后缀链接构成一棵根节点为 $T$ 的树。

定义后缀路径 $p\to q$ 表示在后缀链接构成的树中 $p\to q$ 的路径。

引理 5：通过 $\mathrm{endpos}$ 集合构造的树（每个子节点的 $subset$ 都包含在父节点的 $subset$ 中）与通过后缀链接 $\mathrm{link}$ 构造的树相同。

（图片来源于 OI-Wiki）

引理 6：对于一个状态 $t$，$\mathrm{substr}(t)$ 中所有子串后面接上同一个字符 $c$ 之后，新的子串仍然都属于同一个状态（如果该状态存在）。

假设存在两个字符串 $s_p,s_{p'}\in \mathrm{substr}(t)$ 满足 $\mathrm{endpos}(s_p+c)\neq \mathrm{endpos}(s_{p'}+c)$。不妨设 $\mathrm{endpos}(s_{p'}+c)$ 包含 $\mathrm{endpos}(s_p+c)$ 所没有的一个位置 $pos$，那么 $\mathrm{endpos}(s_{p'})$ 中必定含有 $pos-1$，而 $\mathrm{endpos}(s_p)$ 中必定没有。但是它们属于同一个状态，矛盾。得证。

一些重要的结论：（个人证明，并不非常严谨！）

结论 0：如果我们从任意状态 $t_0$ 开始顺着后缀链接遍历，总会到达初始状态 $T$。这种情况下我们可以得到一个互不相交的区间 $[\mathrm{minlen}(t_i),\mathrm{len}(t_i)]$ 的序列，且它们的并集形成了连续的区间 $[0,\mathrm{len}(t_0)]$。

该引理为 OI-Wiki 在 “小结” 最后一条列出的性质，根据后缀链接的性质和引理 3,4 易证。

结论 1：从表示 $s[1:i]$ 的状态 $t_0$ 不断跳后缀链接 $\mathrm{link}$ 直到初始节点 $T$，其遍历到的所有状态 $t_0,t_1,t_2,\cdots,T$ 所包含的子串集合刚好为所有 $s[1:i]$ 的后缀所表示的状态，即 $\mathrm{substr}(t_0)\cup\mathrm{substr}(t_1)\cup\mathrm{substr}(t_2)\cup\cdots\cup\mathrm{substr}(T)=\{s[x:i]\ (1\leq x\leq i)\}$。换句话说，如果你在 $\mathrm{SAM}_i$ 上跑所有 $s[1:i]$ 的后缀，那么跑到的所有状态都在后缀路径 $t_0\to T$ 上。

证明 1：由后缀链接 $\mathrm{link}$ 的定义，对于任意一个状态 $t_0$，都有 $x$ 是 $y$ 的真后缀，其中 $x\in\mathrm{substr(link}(t_0)),y\in\mathrm{substr}(t_0)$。那么 $S=\mathrm{substr}(t_0)\cup\mathrm{substr}(t_1)\cup\cdots\cup\mathrm{substr}(T)$ 中的所有子串（这里的子串是相对于 $s[1:i]$ 而不是所包含的字符串的子串）都是 $\mathrm{longest(t_0)}$ 即 $s[1:i]$ 的后缀。又根据结论 0，$S$ 中所有字符串长度覆盖了区间 $[0,\mathrm{len}(t_0)]$，即 $[0,i]$。得证。

结论 2：一个状态 $t$ 所表示的所有子串 $\mathrm{substr}(t)$，等于初始状态 $T$ 到该状态上所有路径所形成的所有字符串。如果添加一条转移边 $(p,q)$，字符为 $c$，那么相当于将 $\mathrm{substr}(p)$ 中所有子串末尾加上字符 $c$ 添加到 $\mathrm{substr}(q)$ 里面。

可以结合引理 6 与结论 1 感性理解（其实是我不太会证明，但是它满足这个性质）。如果想要直观理解可以看下文 Case 2 中的插图。

结论 3：考虑存在一个转移 $(p,q)$ 且 $\mathrm{len}(p)+1=\mathrm{len}(q)$，那么其他所有指向 $q$ 的转移 $(p_i,q)$ 的 $p_i$ 都在后缀路径 $p\to T$ 上。

证明 3：首先，根据结论 2，我们知道如果存在转移 $(p,q)$，字符为 $c$，那么一定有 $\mathrm{len}(p)+1\leq\mathrm{len}(q)$。因此，假设有另外一个状态 $p'$ 存在转移 $(p',q)$ 且 $p'$ 不在后缀路径 $p\to T$ 上（显然 $p'$ 不能为 $p$），那么有 $\mathrm{len}(p')< \mathrm{len}(p)$。设 $s_{p}=\mathrm{longest}(p),s_{p'}=\mathrm{longest}(p')$。因为 $s_p+c$ 与 $s_{p'}+c$ 同属于 $\mathrm{substr}(q)$，且 $|s_{p'}+c|<|s_p+c|$，所以根据引理 3，$s_{p'}+c$ 是 $s_p+c$ 的后缀。所以 $s_{p'}$ 是 $s_p$ 的后缀。因此，根据引理 2，$\mathrm{endpos}(s_p)\subsetneq \mathrm{endpos}(s_{p'})\ (p\neq p')$。因此，根据引理 5，$p'$ 在 $\mathrm{link}$ 树上一定为 $p$ 的父节点。这与假设矛盾。得证。

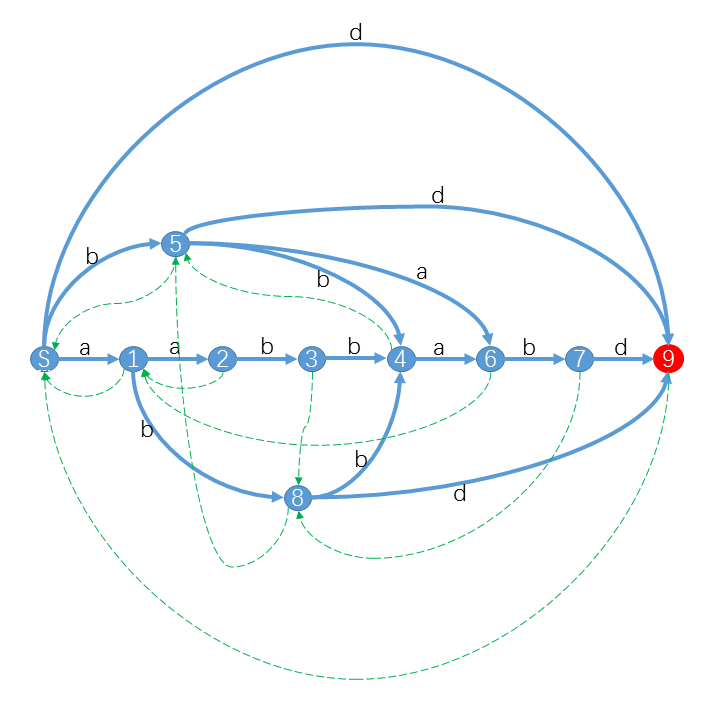
结合上图以更好理解（图片来源于 hihoCoder）。

推论 3：指向状态 $q$ 的转移 $(p_i,q)$ 的所有状态 $p_i$，在 $\mathrm{link}$ 树上一定为一条深度递减的链 $p_0\to p_x$，且有 $\mathrm{minlen}(p_x)+1=\mathrm{minlen}(q),\mathrm{len}(p_0)+1=\mathrm{len}(q)$。

SAM 的构造方式：

类似数学归纳法：假设已经构造好了 $\mathrm{SAM}_{i-1}$，其状态为 $las$，这样所需要做的就是添加一个字符 $s_i$。

首先，$\mathrm{SAM}_{i-1}$ 是无法表示 $s[1:i]$ 的（因为它只接受 $s[1:i-1]$ 的子串），所以我们新建一个节点 $cur$ 表示至少包含 $s[1:i]$ 的状态，显然有 $\mathrm{len}(cur)=i$（或者说等于 $\mathrm{len}(las)+1$）。可以发现 $\mathrm{endpos}(s[1:i])=\{i\}$，因为 $s[1:i]\in\mathrm{substr}(cur)$，而 $s[1:i]$ 在 $s[1:i]$ 中显然只以 $i$ 为结束位置出现。

为什么说至少包含？因为 $s[1:i]$ 的其它后缀也可能只以 $i$ 为结束位置出现。例如 $s=\texttt{aab}$（假设 $i=3$），那么不仅是 $\mathrm{endpos}(\texttt{"aab"})=\{3\}$，$\texttt{"ab"}$ 与 $\texttt{"b"}$ 的 $\mathrm{endpos}$ 集合也为 $\{3\}$。

Case 1：根据引理 1 与 2，如果不考虑重复状态，那我们只需要将后缀路径 $las\to T$ 上的所有状态往 $cur$ 连一条字符为 $s_i$ 的转移边，并将 $\mathrm{link}(cur)$ 设为 $T$ 即可（因为后缀路径 $las\to T$ 上的所有点刚好表示了 $s[1:i-1]$ 的所有后缀，在其后面添加字符 $s_i$ 就可以表示 $s[1:i]$ 的所有后缀）。这其实是 Case 1，即后缀路径 $las\to t$ 上所有状态都没有字符 $s_i$ 的转移边。容易发现这种情况仅在 $s_i$ 未在 $s[1:i-1]$ 中出现过时发生。

如果有重复怎么办？我们从 $las$ 开始跳到的不重复的所有状态往 $cur$ 连一条 $s_i$ 的转移边，并设遇到的第一个重复的转移为 $(p,q)$。为什么不能再添加 $(p,cur)$ 的 $s_i$ 的转移了？因为这样会导致从 $T\to q$ 和 $T\to cur$ 可以表示相同的子串，破坏了 SAM 的性质。记在后缀路径 $las\to T$ 跳到 $p$ 的上一个状态为 $p'$（即 $\mathrm{link}(p')=p$）。显然 $(p',cur)$ 有一条字符为 $s_i$ 的转移。

此时 $cur$ 的后缀链接应该怎么连？我们想要满足 $\mathrm{len(link(}cur))+1=\mathrm{minlen}(cur)$。这个 $\mathrm{minlen}(cur)$ 实际上就是 $\mathrm{minlen}(p')+1$，那么 $\mathrm{len}(p)=\mathrm{minlen}(p')-1=\mathrm{len(link(}cur))-1$（因为 $\mathrm{link}(p')=p$）。

Case 2：$\mathrm{len}(q)=\mathrm{len}(p)+1$，此时 $q$ 中包含的最长子串就是 $p$ 中的最长子串接上字符 $s_i$。那么只需将 $\mathrm{link}(cur)\gets q$ 即可。因为 $\mathrm{len}(q)=\mathrm{len}(p)+1=\mathrm{len(link(}cur))$，刚好是我们想要的。

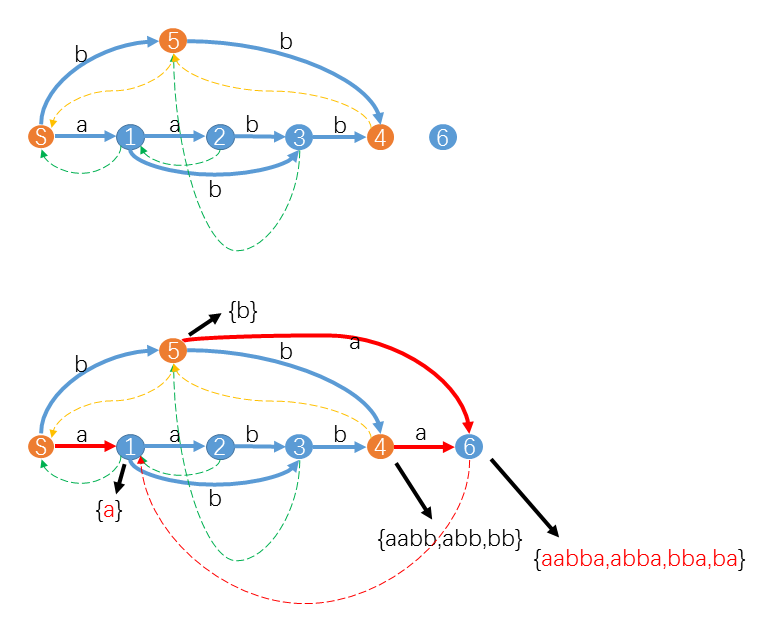
（图片来源于 hihocoder）

上图中，在添加 $s_5=\texttt{a}$ 时，从 $T(S)\to 1$ 已经有了现成的字符 $s_5$ 的转移。此时 $p=T,q=1$。因为 $\mathrm{len}(1)=\mathrm{len}(T)+1\ (1=0+1)$，所以直接将 $\mathrm{link}(6)\gets 1$ 即可。

注意上图中状态 $4,5,6$ 所表示的子串，可以发现状态 $6$ 所表示的子串是状态 $4,5$ 所表示的所有子串后接上字符 $s_5$ 得到的。这很好地验证了结论 2，也非常直观形象地阐释了 Case 2 的情况。

Case 3：$\mathrm{len}(q)>\mathrm{len}(p)+1$，此时 $q$ 对应了 $s[1:i-1]$ 的更长的子串（感觉 OI-Wiki 这里讲得不是很明白）。此时除了把 $q$ 拆开来别无他法。具体来说，将 $q$ 所表示的所有长度不大于 $\mathrm{len}(p)+1$ 的子串提出来，丢给一个新建的状态 $q'$，然后将 $\mathrm{link(cur)}\gets q'$，同时添加转移 $(q',cur)$，也就是说我们凭空创造了一个满足 Case 2 的状态 $q$。

显然，无中生有是要付出一些时间代价的。先考虑 $q$ 和 $q'$ 的内部情况。具体的，$\mathrm{link}(q)$ 应改为 $q'$，而 $\mathrm{link}(q')$ 应该继承原来的 $\mathrm{link}(q)$。此外，一些本来转移到 $q$ 的转移 $(p_i,q)$ 也应该变为 $(p_i,q')$。具体地，我们从后缀路径 $p\to T$ 继续往上跳，沿路径跳到的所有状态 $p_i$，如果有一条 $(p_i,q)$ 的转移，那么将其改为 $(p_i,q')$。

（图片来源于 hihocoder）

特别的，如果跳到一个状态 $P$，它没有 $(P,q)$ 的转移，此时退出即可，因为根据结论 3，此时再往上跳也不可能出现另外一个状态 $P'$ 有 $(P',q)$ 的转移。换句话说，我们找到后缀路径 $p\to T$ 上从 $p$ 开始的一段有 $(p_i,q)$ 转移的所有状态，并将其修改为 $(p_i,q')$。因为根据推论 3，路径上有且仅有一段状态 $p_i$ 有 $(p_i,q)$ 的转移，且所有 $p_i$ 所表示的子串加上字符 $s_i$，刚好能表示状态 $q$ 原本所表示的所有长度不大于 $\mathrm{len(p)}+1$ 的子串，如上图。

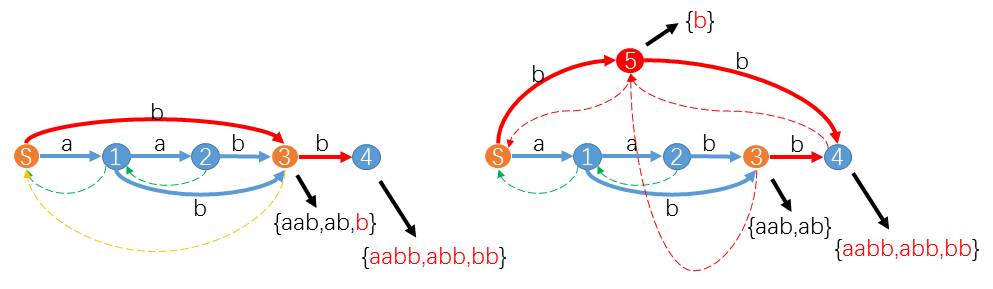
（图片来源于 hihocoder）

上图中，我们把 $q=3$ 的不大于 $\mathrm{len}(T)+1=1$ 的所有子串提出来，丢给一个新建的状态 $q'=5$，然后 $\mathrm{link}(4\ (cur))\gets 5\ (q')$ 并添加状态 $(5,4)$（即 $(q',cur)$）。内部，$\mathrm{link}(3\ (q))\gets 5\ (q')$，同时 $\mathrm{link}(5\ (q')) \gets T$（原来的 $\mathrm{link}(3)$）。最后从 $T\ (p)$ 往上跳后缀连接直到不存在连向 $3$ 的路径或到了初始状态 $T$（当然，这里的例子只有 $T$ 一个点，不过我们需要知道并不一定会跳到 $T$，因为有可能跳到中间的某个状态 $P$ 时就没有转移 $(P,3\ (q))$ 了），并将所有连向 $3\ (q)$ 的转移连向 $5\ (q')$，即 $(T,3)$ 变为了 $(T,5)$。

综合上述三种情况，我们就可以在线性时间内建造出一个字符串 $s$ 的 SAM（关于其时间复杂度为线性的证明，详见 OI-Wiki）。

部分额外信息在代码与应用中有提到。

代码与应用：

请移步 SAM 做题笔记。

一些资料：

如发现错误或有不理解的地方可以在下方评论区留言，我会尽快修改。