LeetCode---105. 从前序与中序遍历序列构造二叉树 （Medium）

题目：105. 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。

注意:

你可以假设树中没有重复的元素。

例如，给出

前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]

返回如下的二叉树：

    3
   / \
  9  20
    /  \
   15   7

第一种解法：递归解

首先

前序遍历： 根 -> 左-> 右

中序遍历：左 -> 根 -> 右

从前序遍历我们可以知道第一个元素3是根节点，再根据中序遍历我们可以知道从第1个元素到根节点3之间的元素是全部都是根节点的左子树，那么我们就可以从中序遍历来得知该根节点左子树元素的个数，假设为x，从而可以得出根节点左子树元素在前序遍历中的区间是多少，而在知道左子树区间之后，根节点右子树在前序遍历中的区间我们也可以知道，参照下图去理解

比如说下面这棵树：

前序遍历：3  9  6  8  20  15  7
中序遍历：6  9  8  3  15  20  7

       3
     /   \
    9     20
   / \    / \
  6   8  15  7

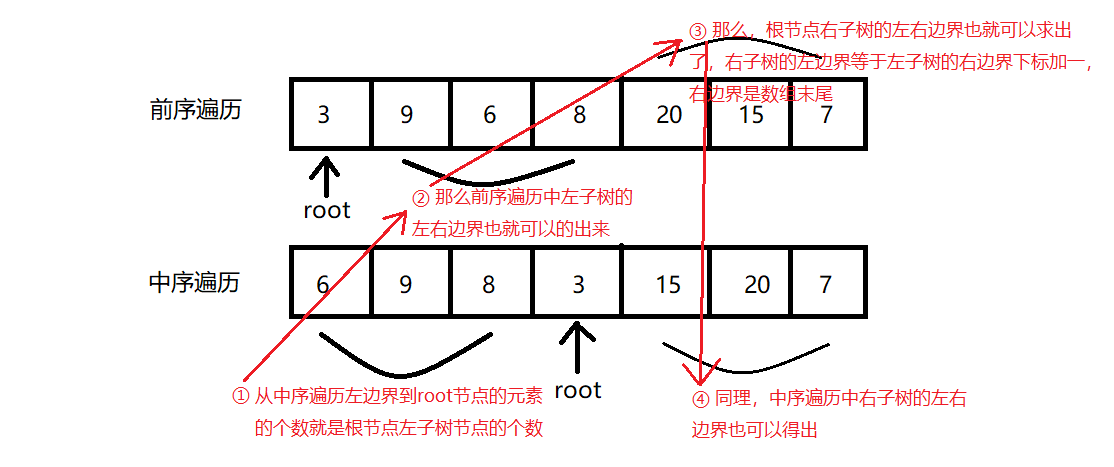
根据代码进一步去理解

代码

class Solution {
    // 递归解
    int[] preorder;
    Map<Integer, Integer> map = new HashMap<>();

    public TreeNode buildTree(int[] preorder, int[] inorder) {
        int len = preorder.length;
        this.preorder = preorder;
        //将中序遍历所有值放在哈希表中，以减少每次在中序遍历中寻找root值下标的时间，空间换时间
        for (int i = 0; i < len; i++) {
            map.put(inorder[i], i);
        }
        return buildTree(0, len - 1, 0, len - 1);
    }

    /**
     * @param preLeft  : 前序遍历左边界
     * @param preRight : 前序遍历右边界
     * @param inLeft   : 中序遍历左边界
     * @param inRight  : 中序遍历右边界
     * @return
     */
    private TreeNode buildTree(int preLeft, int preRight, int inLeft, int inRight) {
        // 递归终止条件，如果左边界大于右边界，递归终止，开始向上一层返回结果
        if (preLeft > preRight || inLeft > inRight) {
            return null;
        }
        // 获取当前根节点的值
        int temp = preorder[preLeft];
        // 创建根节点
        TreeNode root = new TreeNode(temp);
        // 获取根节点在中序遍历中的下标值
        int pIndex = map.get(temp);
        // 递归获取当前根节点的左子树
        // 其中 前序遍历左子树的右边界 = pIndex - 1 - inLeft + preLeft + 1 = pIndex - inLeft + preLeft
        root.left = buildTree(preLeft + 1, pIndex - inLeft + preLeft, inLeft, pIndex - 1);
        // 递归获取当前根节点的右子树
        root.right = buildTree(pIndex - inLeft + preLeft + 1, preRight, pIndex + 1, inRight);
        return root;
    }
}

第二种解法：迭代

迭代是一种很巧妙地的解法

继续看下面这颗树

前序遍历：3  9  6  8  20  15  7
中序遍历：6  9  8  3  15  20  7

       3
     /   \
    9     20
   / \    / \
  6   8  15  7

首先，我们先只看前序遍历

1. 遇到第一个元素3,那么3肯定是作为根节点
2. 遇到第二个元素9，那么9可能是左子树也可能是右子树，此时我们结合中序遍历来看，中序遍历的第一个元素是6,那么我们就可以确定9是左子树，因为假如9是右子树，那么中序遍历的第一个元素应该是根节点3,但此时很明显不是3，所以可以确定9是左子树
3. 再继续往前走，遇到了元素6，同理，6是元素9的左子树，但此时我们发现6与中序遍历第一个元素相等了，这说明左子树已经遍历到了末尾，下一个元素只能是右子树，但究竟是元素6的右子树？还是元素9的右子树？又或者是元素3的右子树？好，我们接着 往下看
4. 现在是遇到了元素8,我们现在有三种情况
   • 第一种情况：元素8是元素6的右子树，那么此时中序遍历的结果就应该是6、8、9、3...
   • 第二种情况：元素8是元素9的右子树，此时中序遍历的结果应该是6、9、8、3...
   • 第三种情况：元素8是元素3的右子树，此时中序遍历的结果是6、9、3、8...
5. 我们知道，第二种情况是与我们的中序遍历结果相符合的，所以当我们倒序遍历已经遇到过的元素时，当前遍历的元素8倒序遍历中最后一个相等的元素9的右子树，而符合可以倒序遍历已经遍历过元素的数据结构就是栈，我们可以用栈来存储已经遍历过的元素。
6. 以此类推，我们可以构造完整棵树

代码

class Solution {
    //迭代，栈，从后往前遍历解
    public TreeNode buildTree2(int[] preorder, int[] inorder) {
        Deque<TreeNode> stack = new ArrayDeque<>();
        int pre = 0;
        int in = 0;
        //构造当前正在遍历的节点
        TreeNode curRoot = new TreeNode(preorder[pre]);
        TreeNode root = curRoot;
        stack.push(curRoot);
        pre++;
        while (pre < preorder.length) {
            if (curRoot.val == inorder[in]) {
                // 如果当前遍历节点值与中序遍历值相等，不断将栈中元素顶出栈，直到值不相等
                while (!stack.isEmpty() && stack.peek().val == inorder[in]) {
                    curRoot = stack.peek();
                    stack.pop();
                    in++;
                }
                // 当前遍历的节点就是最后一个值相等的节点的右子树
                curRoot.right = new TreeNode(preorder[pre]);
                curRoot = curRoot.right;
                stack.push(curRoot);
                pre++;
            } else {
                //如果值不相等就说明是左子树
                curRoot.left = new TreeNode(preorder[pre]);
                curRoot = curRoot.left;
                stack.push(curRoot);
                pre++;
            }
        }
        return root;
    }
}

拓展

趁着手热，可以去做一下这道题：106. 从中序与后序遍历序列构造二叉树