Understanding and Improving Fast Adversarial Training

目录

• 概
• 主要内容
• Random Step的作用
• 线性性质
• gradient alignment
• 代码

Andriushchenko M. and Flammarion N. Understanding and improving fast adversarial training. In Advances in Neural Information Processing Systems (NIPS), 2020.

概

本文主要探讨:

1. 为什么简单的FGSM不能够提高鲁棒性;
2. 为什么FGSM-RS(即加了随机扰动)可以更好地提高鲁棒性;
3. 一种正则化方法, 即使不加随机扰动亦可提高鲁棒性.

主要内容

对抗训练是迄今最有效的防御手段, 其思想为:

\[\min_{\theta} \: \mathbb{E}_{(x, y) \sim D} [\max_{\|\delta\| \le \epsilon} \ell(x + \delta, y ;\theta) ].
\]

为了求解inner maximum, 一般通过PGD来近似求解. 但是这种multi-steps的方法很耗时, 所以最近也有一些方法基于FGSM进行一些改进, 其发现是FGSM在额外加一个扰动之后可以有效提高网络鲁棒性:

\[\delta_{FGSM-RS} := \prod_{[-\epsilon, \epsilon]^d} [\eta + \alpha \mathrm{sign} (\nabla_x \ell(x + \eta, y; \theta))], \: \eta \sim \mathcal{U}([-\epsilon, \epsilon]^d).
\]

但是作者发现这种方法所带来的鲁棒性作用范围(\(\epsilon\))非常狭窄:

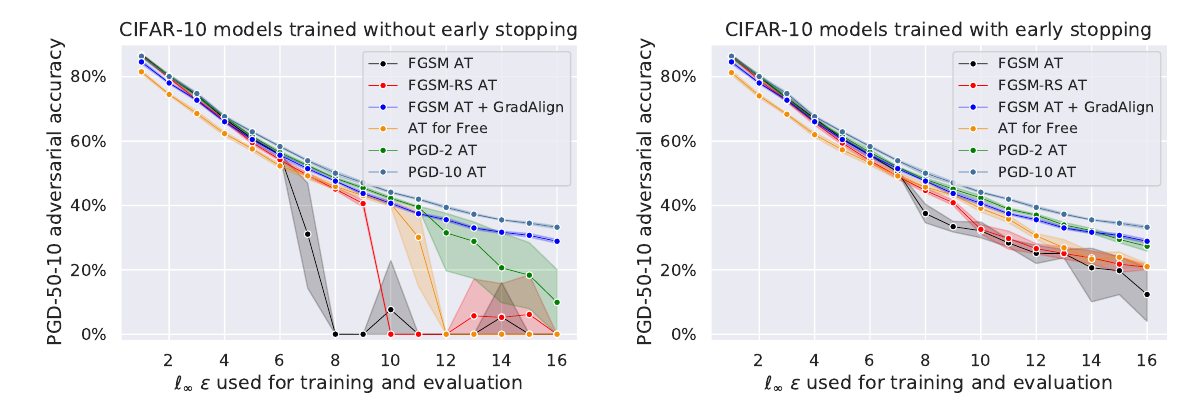
其和FGSM-AT一样, 会在某个点鲁棒性突然崩溃, 没有很好的扩展性.

Random Step的作用

为什么RS能起到一定作用, 作者认为实际上加了RS之后, \(\epsilon\)在某种意义是'变小'了,

作者推得

\[\mathbb{E}_{\eta} [\|\delta_{FGSM-RS}(\eta)\|_2] \le \sqrt{d}\sqrt{-\frac{1}{6\epsilon}\alpha^3 + \frac{1}{2}\alpha^2 + \frac{1}{3}\epsilon} \in [\frac{1}{\sqrt{3}}\sqrt{d}\epsilon, \sqrt{d}\epsilon] \le \|\delta_{FGSM}\|_2 = \sqrt{d}\epsilon.
\]

特别的, 作者设定小的\(\epsilon\)试了(且不加RS)发现能与加了RS效果一致:

线性性质

接下来作者提出自己的观点, 剖析FGSM为啥有这些异常的情况出现.

作者认为一开始FGSM是对于inner maximum求解是较为准确的, 但是随着训练的深入, 不准确了, 为什么不准确, 作者认为是\(\ell(x;\theta)\)关于\(x\)并不那么线性了.

我们知道, FGSM实际上是对于线性情况的最优解:

\[\delta_{FGSM} = \arg \max_{\|\delta\|_{\infty} \le \epsilon} \langle \nabla_x \ell(x, y;\theta),\delta \rangle,
\]

当\(\ell\)在\(\epsilon\)球内不那么线性的时候, 这个解就不好了, 可以通过下面的条件来衡量是否线性:

\[\mathbb{E}_{(x, y) \sim D, \eta \sim \mathcal{U}([-\epsilon, \epsilon]^d)} [\cos(\nabla_x \ell(x, y;\theta), \nabla_x \ell(x + \eta, y; \theta))],
\]

如上图所示, 普通的FGSM和FGSM-RS在训练过程中越发变得局部非线性, 所以求解越来越差.

gradient alignment

本文提出的解决方法就是利用上述的条件作为一个正则化项.

个人感觉这个正则化条件比以往的想法子让梯度变小更有趣一点(不局限于光滑性之上).

代码

原文代码