读吴恩达算-EM算法笔记

最近感觉对EM算法有一点遗忘，在表述的时候，还是有一点说不清，于是重新去看了这篇<CS229 Lecture notes>笔记. 于是有了这篇小札.

关于Jensen's inequality不等式:

　　　　

　　Corollary(推论)：

　　如果函数f(x)为凸函数,那么在 f(x) 上任意两点X1,X2所作割线一定在这两点间的函数图象的上方，即：

　　   其中t表示【x1,x2】的位置

举例子： 当t=1/2 ;  1/2*f(x1) + 1/2*f(x2) >= f( 1/2*x1 + 1/2*x2 );

或者我们直接抽象的表示为： E[f(X)] ≥ f(EX) ，其中E表示期望.

那么这个 Jensen's inequality（Jensen's 不等式在EM算法中起到什么作用呢？）这里我们先不表.

关于极大似然评估(MLE)：

　　假定存在一个样本集 D= {x1,x2,...,Xm },为M个独立分布的样本. 假设似然函数为: 联合概率密度函数P(D ; θ) ，其中(P(D ; θ)这种表示相当于P(D),只是存在未知参数θ)

　　我们知道了似然函数之后，将样本数据展开:

　　　　　　　　　　　　　　 P(D ; θ) = p(x1,x2,...,Xm;θ) = ∏^m_i=1 p(xi ; θ)

　　我们令 L( Z ) =  ∏^m_i=1  p(xi ; θ) ,如果存在θi 使得 L(θ)最大，我们认为θi为θ的极大似然估计量,同时我们认为θi(x1,x2,...,xm)为样本集D的极大似然函数估计量

关于求解极大似然函数：

 　　　　　　求使得出现该组样本的概率最大的θ值。

　　　　        θi = argmax(L(θ)) = argmax(  ∏^m_i=1 p(xi ; θ) );

继续回到上面的公式： 

　　　　　　L( θ ) =  ∏^m_i=1 p(xi ; θ); 要使得L(θ)最大，那么对这个公式进一步化解：

　　　　　 等价于：　log( L(θ) ) = log(  ∏^m_i=1  p(xi ; θ) )  =  ∑^m _i=1 P(xi ;θ)  

　　　　　　　(∑^m _i=1 P(xi ;θ))' = d( ∑^m _i=1 P(xi ;θ) ) / d(θ) =0 ; 求导 得 θ的解   　　　　　　　　　  　　　　　　　　　 

关于极大似然求解的步骤：

　　　（1）写出似然函数；

（2）对似然函数取对数，并整理；

（3）求导数；

（4）解似然方程。

我们先来看文章给出的这样一个问题：

　　　　 比如我们有一个训练集合X={ x1 , x2 , .... , Xm};里面包含M个样本. 我们希望将模型p(x，z)的参数与训练集合数据进行拟合，其中的函数-对数似然是:

　　　　　　　　

　　  我们想上面求解极大似然函数一样来求解这个似然函数：

　　　　　　　　对它进行微分方程，求导    d( L(θ) ) / d( θ ) =0;  ？ 我们很快就发现无法求解，因为存在新的未知变量Z(隐变量)；如何来解释这个隐变量Z呢？

比如这样一个例子:

　　　　　　比如有A,B两个人比赛随机打靶，每个人每次打4枪，当命中九环以内，包括九环,是记录为1，否则记录为0; 但是由于裁判熬夜玩游戏，比赛完成是，收集比赛结果时，搞混了靶纸。于是整理出如下结果:

靶纸结果

人名	结果
未知	1011
未知	0011
未知	1101
未知	0101
未知	1011
未知	0010
未知	1111
未知	1011

问A命中九环的概率pa，B命中九环的概率pb?

而这里的隐变量Z就是人名的顺序。

面对这个问题，显然使用极大似然函数去正面扛困难重重,EM算法为这个问题，提供了一个很好的思路：

　　　　求解分两步走：

　　　　　　　　 E step 期望阶段：

　　　　　　　　　　　　　　

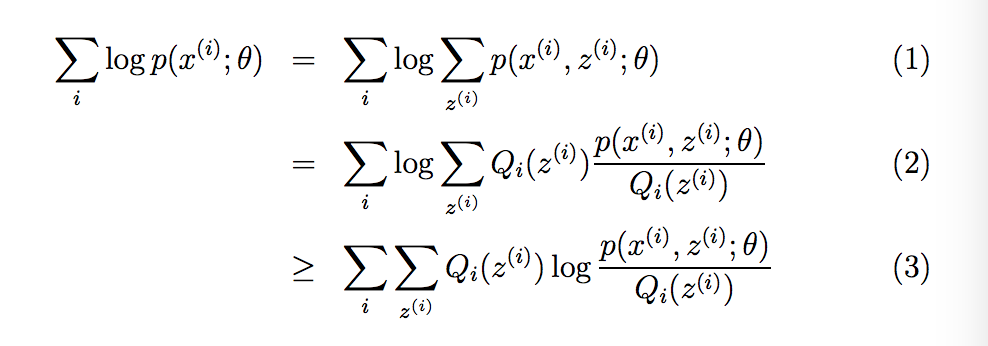
　　　　　　　　　　　　 先假定，即初始化A,B命中的概率pa0=0.2 , pb0=0.5;

　　　　　　　　            求出8次打靶中，该次打靶的结果是A,B的可能性即概率:

　　　　　　　　　　       第一次打靶：如果是A的打靶结果：  0.2*0.8*0.2*0.2=0.0064

　　　　                                           如果是B的打靶结果:    0.5^4 =0.0625

第i次是A,B打靶的结果概率

第i次打靶	A	B
1	0.0064	0.0625
2	0.0256	0.0625
3	0.0064	0.0625
4	0.0256	0.0625
5	0.0064	0.0625
6	0.1024	0.0625
7	0.0016	0.0625
8	0.0064	0.0625

如此，我们依据极大似然函数，来确定每一轮是谁打的

　　1轮: P(A1)<P(B1),

由上面这个表，我们在假定的前提下，计算出了A或者B的出现每轮打靶结果的概率；我们可以依据这个结果，进一步计算第i次是A,B打靶的相对概率

求出8次打靶中，该次打靶的结果是A,B的相对可能性即概率:

　　　　　　　　　　       第一次打靶：如果是A的打靶结果：  0.0064/(0.0064 + 0.0625) =0.0928

　　　　                                           如果是B的打靶结果:    0.0625/(0.0064 + 0.0625) =0.9072

第i次是A,B打靶结果的概率

第i次打靶	A	B
1	0.0928	0.9072
2	0.290	0.710
3	0.0928	0.9072
4	0.290	0.710
5	0.0928	0.9072
6	0.620	0.380
7	0.0249	0.9751
8	0.0928	0.9072

　　　　我们先假定A，B命中的概率pa1,pb1，然后去推到它们比赛的顺序，再依据比赛的顺序，来计算A,B命中的概率Pa2,pb2. 当pa2,pb2和pa1,pb2结果相差时较大时，

将pa2,pb2代入，继续推到它们的比赛顺序，计算A,B命中的概率