题解【bzoj4650 [NOI2016]优秀的拆分】

Description

求对每一个连续字串将它切割成形如 AABB 的形式的方案数之和

Solution

显然 AABB 是由两个 AA 串拼起来的

考虑维护两个数组 a[i] 和 b[i] ，其中 a[i] 表示以 $i$ 结尾有多少个 AA 串，b[i] 表示以 $i$ 开头有多少个 AA 串

最后答案就是 $\sum \limits _{i=1}^{n-1}a[i]b[i+1]$ （就是两个串拼起来）

如何求 a[i] 和 b[i] 呢？

首先有一个非常显然的 n^2 哈希做法（对于每一个 $i$ 用 $j$ 扫一遍用哈希判断有几个 AA 串），有 95 分！

如何拿到最后的 5 分呢？考虑枚举一个 Len ，然后对于每个点求出他是否是一个 2 * Len 的 AA 串的开头 / 结尾。

我们每隔 Len 放一个点，这样每一个长度为 2 * Len 的 AA 串都至少会经过两个相邻的点。

所以再转换为每两个相邻的点会对 a, b 产生多少贡献。

先求出这对相邻点所代表的前缀的最长公共后缀 LCS 和所代表的后缀的最长公共前缀 LCP

如果 LCP + LCS < Len 就下面这种情况：

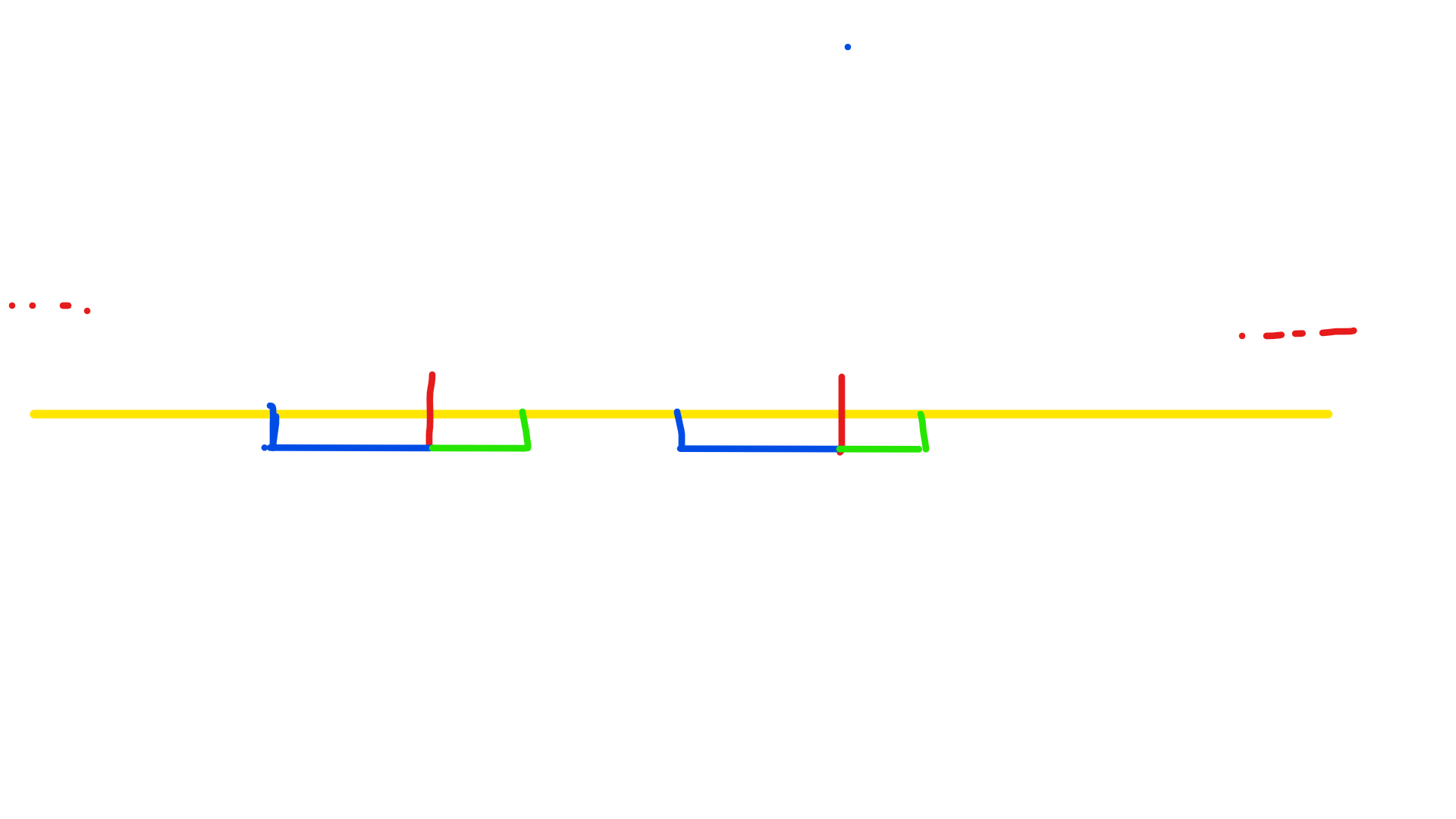
其中两个红线是关键点（相距为 Len），蓝线是LCS，绿线是LCP，LCP+LCS < Len

则有

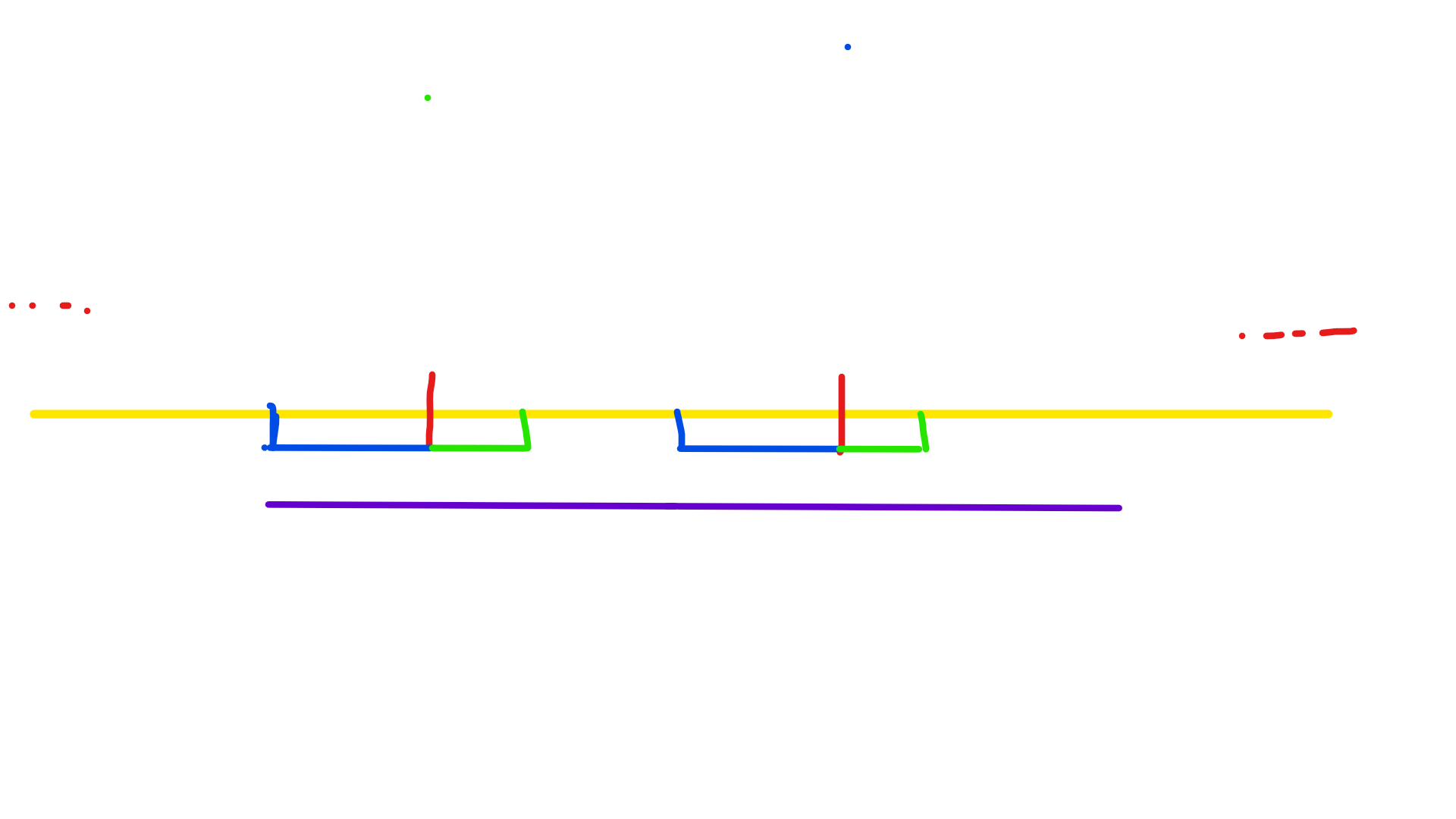
这条紫线就是第一个可能满足条件的 AA 串

但此时我们会发现下图

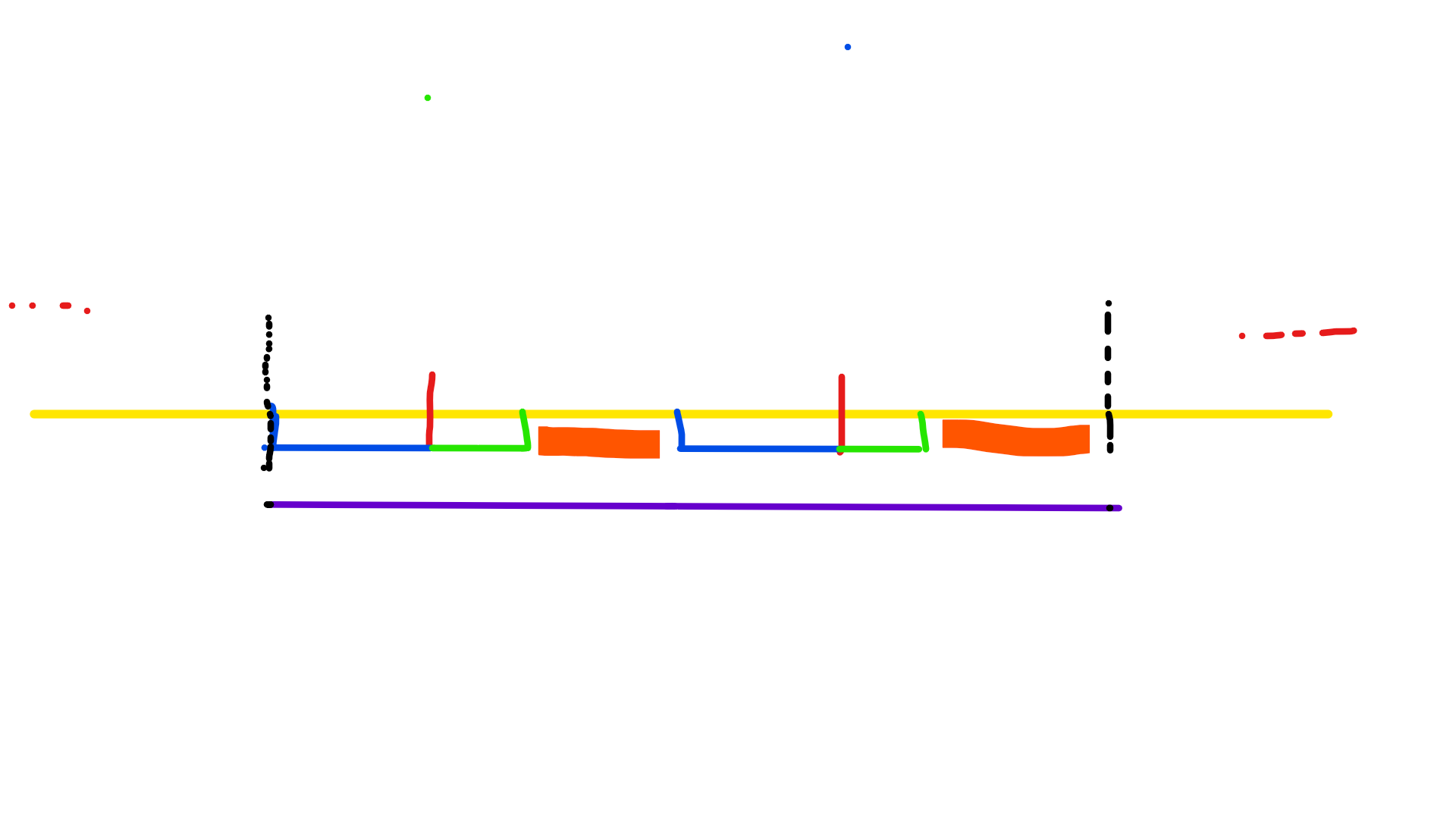
其中两个红色荧光笔的部分在 AA 串中是对应的，但他们至少有一个位置并不相同（不然LCP可以再长）

所以此时不会有任意一个长度为 2 * Len 的 AA 串满足条件。

如果 LCP + LCS >= Len 就有下面这种情况

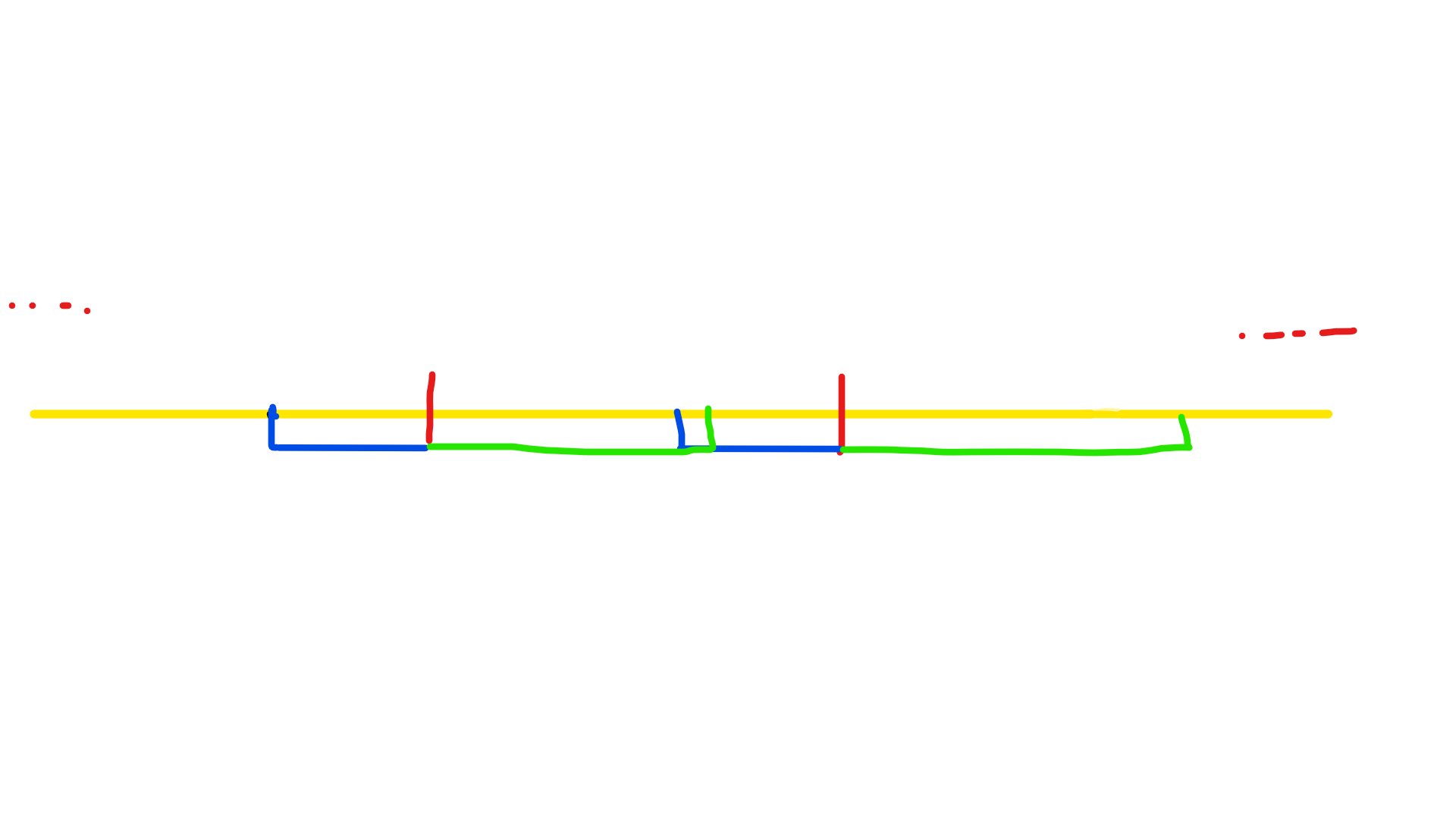
此时中间必然就没有空隙。可以发现：

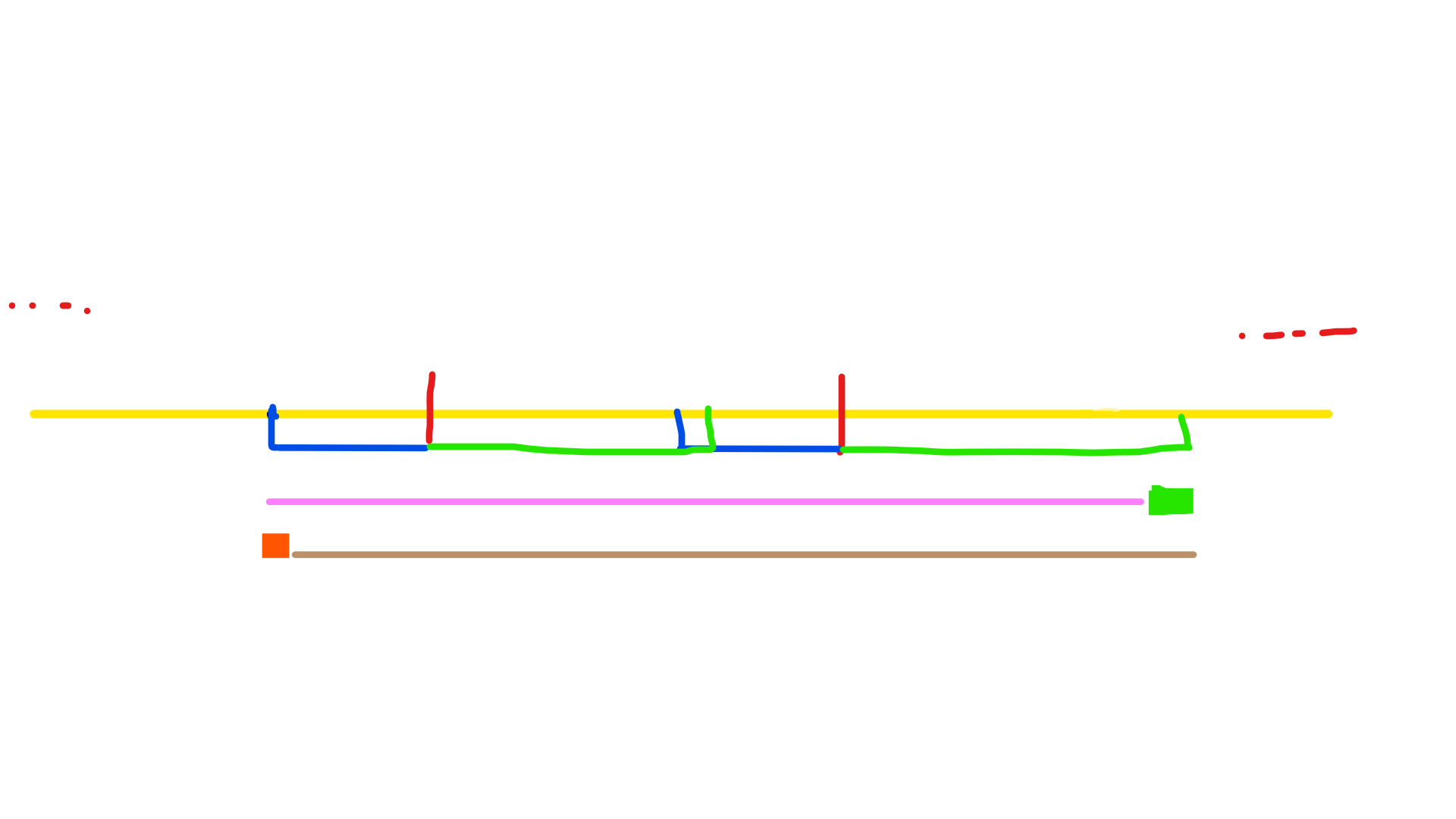
粉色的是第一个 AA 串，可以发现它是可以分成两个相同的 A 串的（可以理解成中间没有缝隙了所以就没有不一样的了）

然后这个 AA 串可以一直往后滑动，每滑动一个位置都可以形成一个新的 AA 串知道 AA 串的后端点滑动到最右边的绿色端点。也就是滑动到棕色 AA 串

此时可以发现，每一个存在于红色荧光部分的点都可以作为一个新的 AA 串的开头

同理，每一个再绿色荧光笔的点可以作为一个新的 AA 串的结尾。

于是就将红色荧光笔的区间的 b 加上 1，绿色的 a 加上 1，就大功告成。

如何实现这个过程呢？复杂度是什么呢？

枚举 Len ，每隔 Len 设置关键点：这个的复杂度是调和级数 $O(n \log n)$
求后缀LCP，前缀LCS：使用后缀数组 + st 表做到 O(1) 查询
区间加上 1 ：差分维护就可以了。

至此，此题完结

Code

#include <bits/stdc++.h>

#define ll long long

using namespace std;

const int N = 1001000;

int T;

ll a[N], b[N];

struct SuffixArray {

  char S[N]; int n;

  int cnt[N], sa[N], rk[N], height[N];

  int st[N][25], lg2[N];

  struct node {

    int id, x, y;

  }aa[N], bb[N];

  inline void buildsa() {

    n = strlen(S + 1);

    memset(cnt, 0, sizeof(cnt));

    memset(height, 0, sizeof(height));

    memset(sa, 0, sizeof(sa));

    memset(rk, 0, sizeof(rk));

    for(int i = 1; i <= n; i++) aa[i].id = bb[i].id = aa[i].x = aa[i].y = bb[i].x = bb[i].y = 0;

    for(int i = 1; i <= n; i++) cnt[S[i]] = 1;

    for(int i = 1; i <= 256; i++) cnt[i] += cnt[i - 1];

    for(int i = 1; i <= n; i++) rk[i] = cnt[S[i]];

    for(int L = 1; L < n; L *= 2) {

      for(int i = 1; i <= n; i++) aa[i].id = i, aa[i].x = rk[i], aa[i].y = rk[i + L];

      for(int i = 1; i <= n; i++) cnt[i] = 0;

      for(int i = 1; i <= n; i++) cnt[aa[i].y]++;

      for(int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];

      for(int i = n; i >= 1; i--) bb[cnt[aa[i].y]--] = aa[i];

      for(int i = 1; i <= n; i++) cnt[i] = 0;

      for(int i = 1; i <= n; i++) cnt[aa[i].x]++;

      for(int i = 1; i <= n; i++) cnt[i] += cnt[i - 1];

      for(int i = n; i >= 1; i--) aa[cnt[bb[i].x]--] = bb[i];

      for(int i = 1; i <= n; i++)

        if(aa[i].x == aa[i - 1].x && aa[i].y == aa[i - 1].y)

          rk[aa[i].id] = rk[aa[i - 1].id];

        else rk[aa[i].id] = rk[aa[i - 1].id] + 1;

    } for(int i = 1; i <= n; i++) sa[rk[i]] = i; int k = 0;

    for(int i = 1; i <= n; i++) {

      if(k) k--;

      int j = sa[rk[i] - 1];

      while(i + k <= n && j + k <= n && S[i + k] == S[j + k]) k++;

      height[rk[i]] = k;

    }

  }

  inline void buildst() {

    lg2[0] = -1; for(int i = 1; i < N; i++) lg2[i] = lg2[i / 2] + 1; lg2[0] = 0;

    for(int i = 1; i <= n; i++) st[i][0] = height[i];

    for(int j = 1; (1 << j) <= n; j++)

      for(int i = 1; i + (1 << j) - 1 <= n; i++)

        st[i][j] = min(st[i][j - 1], st[i + (1 << (j - 1))][j - 1]);

  }

  inline int Lcp(int l, int r) {

    l = rk[l], r = rk[r];

    if(l > r) swap(l, r); l++;

    int k = lg2[r - l + 1];

    return min(st[l][k], st[r - (1 << k) + 1][k]);

  }

}SA[2];

int main() {

  scanf("%d", &T);

  while(T--) {

    scanf("%s", SA[0].S + 1);

    int n = strlen(SA[0].S + 1);

    for(int i = 1; i <= n; i++) a[i] = b[i] = 0;

    for(int i = 1; i <= n; i++)

      SA[1].S[i] = SA[0].S[n - i + 1];

    SA[0].buildsa(), SA[1].buildsa();

    SA[0].buildst(), SA[1].buildst();

    for(int Len = 1; Len <= n / 2; Len++) {

      for(int i = Len; i <= n; i += Len) {

        int l = i, r = i + Len;

        int L = n - (r - 1) + 1, R = n - (l - 1) + 1;

        int lcp = SA[0].Lcp(l, r); lcp = min(lcp, Len);

        int lcs = SA[1].Lcp(L, R); lcs = min(lcs, Len - 1);

        if(lcp + lcs >= Len) {

          b[i - lcs]++, b[i - lcs + (lcp + lcs - Len + 1)]--;

          a[r + lcp - (lcp + lcs - Len + 1)]++, a[r + lcp]--;

        }

      }

    } for(int i = 1; i <= n; i++) a[i] += a[i - 1], b[i] += b[i - 1];

    ll ans = 0; for(int i = 1; i < n; i++) ans += a[i] * b[i + 1];

    printf("%lld\n", ans);

  }

  return 0;

}