codeforces 691E（矩阵乘法）

E. Xor-sequences

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n integers a1,  a2,  ...,  an.

A sequence of integers x1,  x2,  ...,  xk is called a "xor-sequence" if for every 1  ≤  i  ≤  k - 1 the number of ones in the binary representation of the number xi  xi  +  1's is a multiple of 3 and 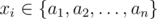 for all 1 ≤ i ≤ k. The symbol  is used for the binary exclusive or operation.

How many "xor-sequences" of length k exist? Output the answer modulo 109 + 7.

Note if a = [1, 1] and k = 1 then the answer is 2, because you should consider the ones from a as different.

Input

The first line contains two integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of given integers and the length of the "xor-sequences".

The second line contains n integers ai (0 ≤ ai ≤ 1018).

Output

Print the only integer c — the number of "xor-sequences" of length k modulo 109 + 7.

Examples

input

5 2
15 1 2 4 8

output

13

input

5 1
15 1 2 4 8

output

5
思路：很好的一道矩阵乘法题，需要建立起模型。先预处理出一个矩阵，第i行j个表示a[i]异或a[j]是否能被3整除，然后再将矩阵计算k-1次幂，最后将矩阵中所有元素加起来。

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<cstring>
#include<string>
#include<vector>
#include<map>
#include<set>
#include<queue>
#define mo 1000000007
using namespace std;
struct Matrix
{
    long long a[][];
};
long long n,k,a[];
Matrix st,ans;
Matrix mul(Matrix a,Matrix b)
{
    Matrix c;
    int i,j,k;
    //<F5>a.a[1][1]=1;
    for (i=;i<=n;i++)
        for (j=;j<=n;j++)
        {
            c.a[i][j]=;
            for (k=;k<=n;k++)
                c.a[i][j]=(c.a[i][j]+(a.a[i][k]*b.a[k][j]%mo))%mo;
        }
    return c;
}
Matrix power(Matrix a,long long b)
{
    Matrix c;
    int i;
    memset(c.a,,sizeof(c.a));
    for (i=;i<=n;i++) c.a[i][i]=;
    while (b)
    {
        if (b&) c=mul(c,a);
        b>>=;
        a=mul(a,a);
    }
    return c;
}
bool can(long long x)
{
    long long ret=;
    while (x)
    {
        ret+=(x&);
        x>>=;
    }
    return (ret%==);
}
int main()
{
    scanf("%lld%lld",&n,&k);
    int i,j;
    for (i=;i<=n;i++) scanf("%lld",&a[i]);
    for (i=;i<=n;i++)
        for (j=;j<=n;j++) st.a[i][j]=can(a[i]^a[j]);
    ans=power(st,k-);
    long long ret=;
    //cout<<ans.a[i][j]<<endl;
    for (i=;i<=n;i++)
        for (j=;j<=n;j++) ret=(ret+ans.a[i][j])%mo;
    printf("%lld\n",ret);
    return ;
}