1）何为随机梯度下降

  • 优化方法
  • 迭代更新，来寻找函数全局最优解的方法
  • 与最小二乘法相比：适用于变量众多，模型更复杂

2）梯度

  • 变化最快，“陡峭”
  • 通过函数表达式来衡量梯度

3）随机梯度下降原理推导过程

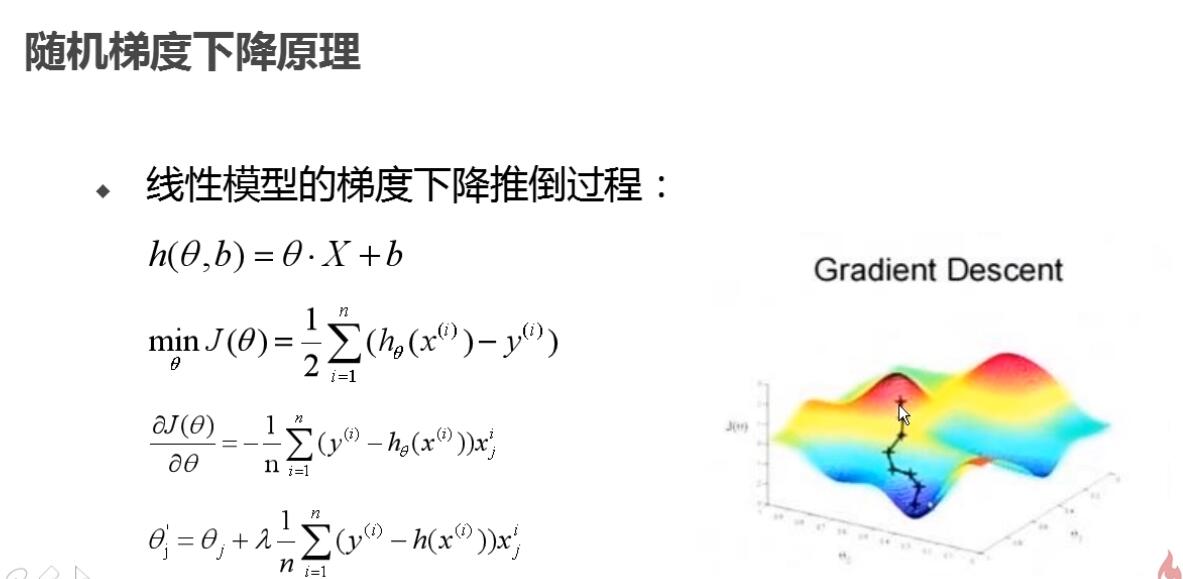
4）随机梯度下降的优点

  • 计算量更小
  • 擅长大量样本
  • 学习率决定了算法速度

掌握Spark机器学习库-07-随机梯度下降的更多相关文章

  1. 掌握Spark机器学习库-07.6-线性回归实现房价预测

    数据集 house.csv 数据概览 代码 package org.apache.spark.examples.examplesforml import org.apache.spark.ml.fea ...

  2. 掌握Spark机器学习库-07.14-保序回归算法实现房价预测

    数据集 house.csv 数据集概览 代码 package org.apache.spark.examples.examplesforml import org.apache.spark.ml.cl ...

  3. 机器学习-随机梯度下降（Stochastic gradient descent）

    sklearn实战-乳腺癌细胞数据挖掘(博主亲自录制视频) https://study.163.com/course/introduction.htm?courseId=1005269003& ...

  4. 机器学习算法（优化）之一：梯度下降算法、随机梯度下降（应用于线性回归、Logistic回归等等）

    本文介绍了机器学习中基本的优化算法—梯度下降算法和随机梯度下降算法,以及实际应用到线性回归.Logistic回归.矩阵分解推荐算法等ML中. 梯度下降算法基本公式 常见的符号说明和损失函数 X :所有 ...

  5. 机器学习-随机梯度下降（Stochastic gradient descent）和 批量梯度下降（Batch gradient descent ）

    梯度下降(GD)是最小化风险函数.损失函数的一种常用方法,随机梯度下降和批量梯度下降是两种迭代求解思路,下面从公式和实现的角度对两者进行分析,如有哪个方面写的不对,希望网友纠正. 下面的h(x)是要拟 ...

  6. 机器学习（ML）十五之梯度下降和随机梯度下降

    梯度下降和随机梯度下降 梯度下降在深度学习中很少被直接使用,但理解梯度的意义以及沿着梯度反方向更新自变量可能降低目标函数值的原因是学习后续优化算法的基础.随后,将引出随机梯度下降(stochastic ...

  7. 掌握Spark机器学习库（课程目录）

    第1章 初识机器学习 在本章中将带领大家概要了解什么是机器学习.机器学习在当前有哪些典型应用.机器学习的核心思想.常用的框架有哪些,该如何进行选型等相关问题. 1-1 导学 1-2 机器学习概述 1- ...

  8. NN优化方法对照：梯度下降、随机梯度下降和批量梯度下降

    1.前言 这几种方法呢都是在求最优解中常常出现的方法,主要是应用迭代的思想来逼近.在梯度下降算法中.都是环绕下面这个式子展开: 当中在上面的式子中hθ(x)代表.输入为x的时候的其当时θ參数下的输出值 ...

  9. 深度学习必备：随机梯度下降（SGD）优化算法及可视化

    补充在前:实际上在我使用LSTM为流量基线建模时候,发现有效的激活函数是elu.relu.linear.prelu.leaky_relu.softplus,对应的梯度算法是adam.mom.rmspr ...

随机推荐

  1. 手机阅读行业SWOT分析

    上个星期,在公司内部的分享活动上给童鞋们分享了手机阅读行业现状,小伙伴儿们嗷嗷待哺的眼神促使我把PPT转换为博客里的文字和图片,再一次更加深入地进入手机阅读. 通过SWOT分析分析我们能够对手机阅读行 ...

  2. Datagrid接收JSON数据格式

    开打View下面的Shared创建一个视图模版(母版页)<!DOCTYPE html> <html> <head> <title>Main</ti ...

  3. [IT学习]Greatwall

    1.evilcos 优雅 过城墙 如果没这个开源的关键解决方案怎么办呢?我给你一个永恒思路,技术贴请看: http://www.ibm.com/developerworks/cn/linux/l-cn ...

  4. 2016/05/25 empty() 与 isset()的区别

    对于初学php的人来说,empty()和和isset()用法的区别是很难搞清楚的,他们的用法的差别不仔细去琢磨的话确实很难弄清楚. 先说一下他们的共同点: 都可以判定一个变量是否为空: 都返回bool ...

  5. test_action

    [TOP] 为什么百度校招数据挖掘工程师的笔试题目是跟数据挖掘关系不大? - 研究生生活交流 - 王道论坛,专注于计算机考研的点点滴滴! http://www.cskaoyan.com/thread- ...

  6. Posting array of JSON objects to MVC3 action method via jQuery ajax

    Does the model binder not suport arrays of JSON objects? The code below works when sending a single ...

  7. c# 32位机和64位机 读取Excel内容到DataSet

    // ----------------------32位机 //注释说明 //ExclePath 为Excel路径 批号 是指Excel文件中某一列必填项 public static DataSet ...

  8. YTU 2405: C语言习题 牛顿迭代法求根

    2405: C语言习题 牛顿迭代法求根 时间限制: 1 Sec  内存限制: 128 MB 提交: 562  解决: 317 题目描述 用牛顿迭代法求根.方程为ax3+bx2+cx+d=0.系数a,b ...

  9. jQuery简单纯文字提示条

    如何制作jQuery简单纯文字提示条,先介绍提示条(tooltip)的意思是用户鼠标悬停经过事件发生提示title.它们已经呈现在大多数浏览器中,当你可以提供一个链接或图片的title属性,就是用户将 ...

  10. 【monkey】

    在Android文件系统中的存放路径是:/system/framework/monkey.jarMonkey.jar 程序是由一个名为“monkey”的Shell脚本来启动执行,shell脚本在And ...