P1140 相似基因 (动态规划)

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了4种核苷酸，简记作A,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATG和GTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

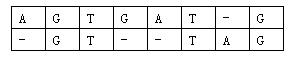
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

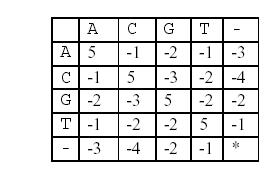
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9。因为两个基因的对应方法不唯一，例如又有：

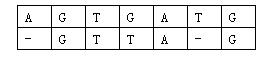
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,T四个字母。1<=序列的长度<=100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1：

7 AGTGATG
5 GTTAG

输出样例#1： 

  14

 

 

Solution

这道题的思路算比较简单.

状态定义可以很快想出来.即用 f[ i ][ j ] 表示匹配到前一个DNA序列的 第 i 个和第二个DNA串的 第 j 个的最大相似度.

然后前导状态也很容易想:

1.  f [ i-1 ][ j-1 ]  此时即用当前两个DNA排在一起. 加上这两个的相似度.

2.  f [ i-1 ][ j ] 此时即 前一个DNA序列的第 i 个和空格匹配.

3.  f [ i ][ j-1 ] 此时即 后一个DNA序列的第 j 个和空格匹配.

然后这道题的预处理其实才是最坑的.

因为它有可能前面一整个字符串都用空格匹配.

代码

#include<bits/stdc++.h>
using namespace std;
int c[][]={
,-,-,-,-,
-,,-,-,-,
-,-,,-,-,
-,-,-,,-,
-,-,-,-,,
};
int n,m;
int nn[],mm[];
int f[][];
int main()
{
    cin>>n;
    for(int i=;i<=n;i++)
    {
        char ch; cin>>ch;
        if(ch=='A')nn[i]=; if(ch=='C')nn[i]=;
        if(ch=='G')nn[i]=; if(ch=='T')nn[i]=;
    }
    cin>>m;
    for(int i=;i<=m;i++)
    {
        char ch; cin>>ch;
        if(ch=='A')mm[i]=; if(ch=='C')mm[i]=;
        if(ch=='G')mm[i]=; if(ch=='T')mm[i]=;
    }

    for(int i=;i<=n;i++)
    f[i][]=f[i-][]+c[][nn[i]];
    for(int i=;i<=m;i++)
    f[][i]=f[][i-]+c[][nn[i]];
    //预处理部分
    for(int i=;i<=n;i++)
    for(int j=;j<=m;j++)
        f[i][j]=max(f[i-][j-]+c[nn[i]][mm[j]],max(f[i-][j]+c[][nn[i]],f[i][j-]+c[][mm[j]]));
    cout<<f[n][m]<<endl;
}