Palindrome Partitioning （回文子串题）

Given a string s, partition s such that every substring of the partition is a palindrome.

Return all possible palindrome partitioning of s.

For example, given s = "aab",
Return

  [
    ["aa","b"],
    ["a","a","b"]
  ]

题意理解：就是把一个字符串进行切割，要求切割之后的子串是回文串。

思路步骤：1.回文字符串划分 2.动态规划生成回文字符串数组 3.根据dp数组用深度搜索生成回文字符串的划分

简单描述一下，首先用动态规划的方法记录出dp[i][j]是否为回文子串（是为1，否则为0）。dp[i][j]表示字符串s中的索引从i....j的子串是不是回文字符串。

构造dp数组，当i=j时，dp[i][j]=1。

当i不等于j时，要求dp[i][j]只需当s[i]==s[j]且dp[i+1][j-1]=1来判断其余的即可。（i+1和j-1表示子串s[i...j]变为子串s[i+1...j-1],即去掉左右两边）

因此我们得反着来求dp，因为需要用到i+1.

然后根据生成好的dp数组，用dfs对数组进行划分。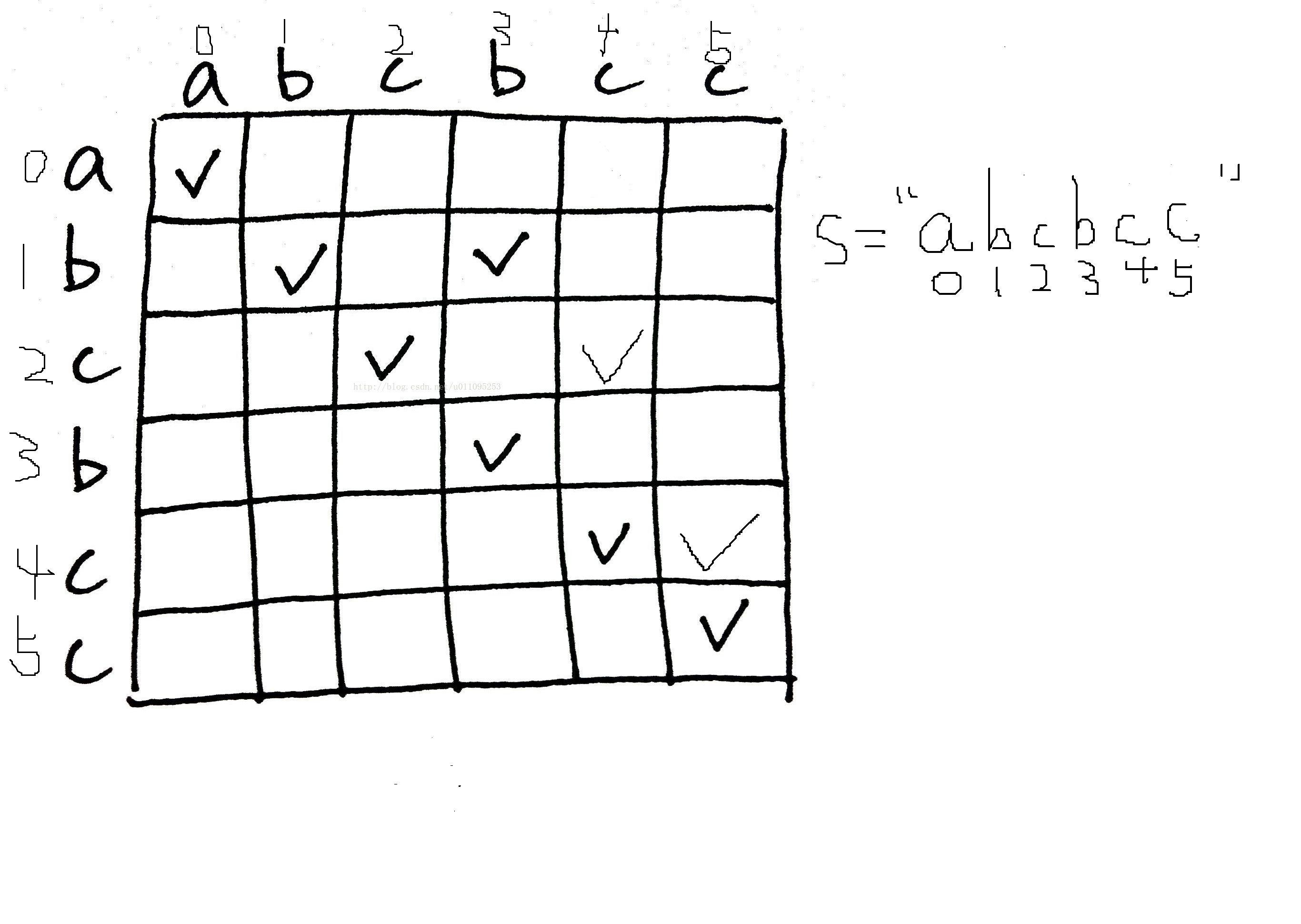




代码：

class Solution {
private:
    int dp[][];
    vector<vector<string>> result;
    void dfs(string s, int begin,vector<string> temp) {
        if(begin==s.length()) {
            result.push_back(temp);
            return;
        }
        for(int i=begin;i<s.length();i++) {
            if(dp[begin][i]==) {
                temp.push_back(s.substr(begin,i-begin+));
                dfs(s,i+,temp);
                temp.pop_back();
            }
        }
    }
    void dp_resolve(string s){
        int n=s.size();
        memset(dp,,sizeof(dp));

        for (int i = n-; i >=; --i)
        {
            for (int j = i; j < n; ++j)
            {
                if(j==i){
                    dp[i][j]=;
                }else if(j==i+){
                    if(s[i]==s[j]) dp[i][j]=;
                }
                else{
                    if(s[i]==s[j]&&dp[i+][j-]) dp[i][j]=;
                }
            }
        }
        vector<string> temp;
        dfs(s,,temp);
        return;
    }
public:
    vector<vector<string>> partition(string s) {
        if(s.empty()) return result;
        dp_resolve(s);
        return result;
    }
};

参考博文：http://blog.csdn.net/worldwindjp/article/details/22042133

　　　　　http://blog.csdn.net/u011095253/article/details/9177451

 类似题目：最长回文子串（Longest Palindromic Substring）
                最长回文子序列