(六)6.9 Neurons Networks softmax regression
SoftMax回归模型,是logistic回归在多分类问题的推广,即现在logistic回归数据中的标签y不止有0-1两个值,而是可以取k个值,softmax回归对诸如MNIST手写识别库等分类很有用,该问题有0-9 这10个数字,softmax是一种supervised learning方法。
在logistic中,训练集由 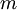 个已标记的样本构成:
个已标记的样本构成: ,其中输入特征
,其中输入特征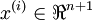 (特征向量
(特征向量  的维度为
的维度为 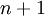 ,其中
,其中 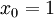 对应截距项 ), logistic 回归是针对二分类问题的,因此类标记
对应截距项 ), logistic 回归是针对二分类问题的,因此类标记 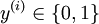 。假设函数(hypothesis function) 如下:
。假设函数(hypothesis function) 如下:
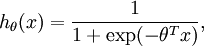
损失函数为负log损失函数:
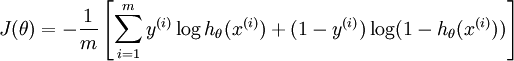
找到使得损失函数最小时的模型参数  ,带入假设函数即可求解模型。
,带入假设函数即可求解模型。
在softmax回归中,对于训练集 中的类标
中的类标  可以取
可以取  个不同的值(而不是 2 个),即有
个不同的值(而不是 2 个),即有 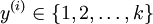 (注意不是由0开始), 在MNIST中有K=10个类别。
(注意不是由0开始), 在MNIST中有K=10个类别。
在softmax回归中,对于输入x,要计算x分别属于每个类别j的概率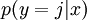 ,即求得x分别属于每一类的概率,因此假设函数要设定为输出一个k维向量,每个维度代表x被分为每个类别的概率,假设函数
,即求得x分别属于每一类的概率,因此假设函数要设定为输出一个k维向量,每个维度代表x被分为每个类别的概率,假设函数 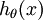 形式如下:
形式如下:
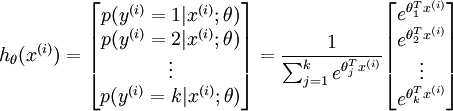
请注意 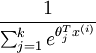 这一项对概率分布进行归一化,使得所有概率之和为 1 。当类别数
这一项对概率分布进行归一化,使得所有概率之和为 1 。当类别数 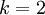 时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当
时,softmax 回归退化为 logistic 回归。这表明 softmax 回归是 logistic 回归的一般形式。具体地说,当 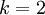 时,softmax 回归的假设函数为:
时,softmax 回归的假设函数为: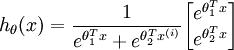 ,对该式进行化简得到:
,对该式进行化简得到:
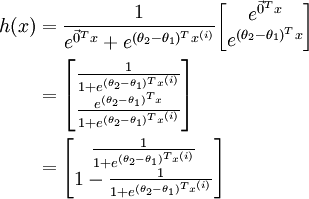
另 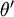 来表示
来表示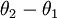 ,我们就会发现 softmax 回归器预测其中一个类别的概率为
,我们就会发现 softmax 回归器预测其中一个类别的概率为 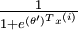 ,另一个类别概率的为
,另一个类别概率的为 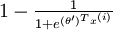 ,这与 logistic回归是一致的。
,这与 logistic回归是一致的。
其中 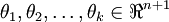 是模型的参数。把参数
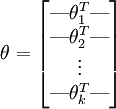
是模型的参数。把参数  表示为矩阵形式有,
表示为矩阵形式有,  是一个
是一个  的矩阵,该矩阵是将
的矩阵,该矩阵是将 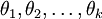 按行罗列起来得到的:
按行罗列起来得到的:
有个假设函数(Hypothesis Function),下面来看代价函数,根据代价函数求解出最优参数值带入假设函数即可求得最终的模型,先引入函数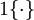 ,对于该函数有:
,对于该函数有:
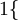 值为真的表达式
值为真的表达式 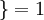
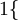 值为假的表达式
值为假的表达式 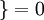 。
。
举例来说,表达式 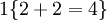 的值为1 ,
的值为1 ,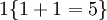 的值为 0 。
的值为 0 。
则softmax的损失函数为:
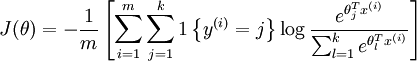
当k=2时,即有logistic的形式,下边是推倒:

另上式中的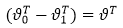 便得到了logistic回归的损失函数。
便得到了logistic回归的损失函数。
可以看到,softmax与logistic的损失函数只是k的取值不同而已,且在softmax中将类别x归为类别j的概率为:
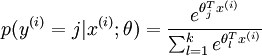 .
.
需要注意的一个问题是softmax回归中的模型参数化问题,即softmax的参数集是“冗余的”。
假设从参数向量  中减去了向量
中减去了向量  ,这时,每一个
,这时,每一个  都变成了
都变成了 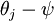 (
(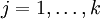 )。此时假设函数变成了以下的式子:
)。此时假设函数变成了以下的式子:
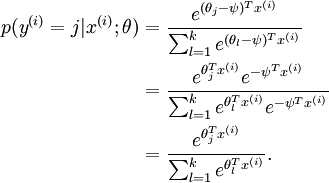
也就是说,从  中减去
中减去  完全不影响假设函数的预测结果,这就说明 Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数
完全不影响假设函数的预测结果,这就说明 Softmax 模型被过度参数化了。对于任意一个用于拟合数据的假设函数,可以求出多组参数值,这些参数得到的是完全相同的假设函数 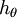 ,也就是说如果参数集合
,也就是说如果参数集合 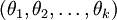 是代价函数
是代价函数  的极小值点,那么
的极小值点,那么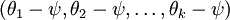 同样也是它的极小值点,其中
同样也是它的极小值点,其中  可以是任意向量,到底是什么造成的呢?从宏观上可以这么理解,因为此时的损失函数不是严格非凸的,也就是说在局部最小值点附近是一个”平坦”的,所以在这个参数附近的值都是一样的了。平坦假设函数空间的Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题。因此使
可以是任意向量,到底是什么造成的呢?从宏观上可以这么理解,因为此时的损失函数不是严格非凸的,也就是说在局部最小值点附近是一个”平坦”的,所以在这个参数附近的值都是一样的了。平坦假设函数空间的Hessian 矩阵是奇异的/不可逆的,这会直接导致采用牛顿法优化就遇到数值计算的问题。因此使  最小化的解不是唯一的。但此时
最小化的解不是唯一的。但此时  仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。
仍然是一个凸函数,因此梯度下降时不会遇到局部最优解的问题。
还有一个值得注意的地方是:当 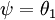 时,我们总是可以将
时,我们总是可以将  替换为
替换为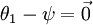 (即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量
(即替换为全零向量),并且这种变换不会影响假设函数。因此我们可以去掉参数向量  (或者其他
(或者其他  中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的
中的任意一个)而不影响假设函数的表达能力。实际上,与其优化全部的 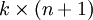 个参数
个参数 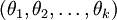 (其中
(其中 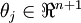 ),我们可以令
),我们可以令 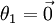 ,只优化剩余的
,只优化剩余的 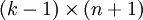 个参数,这样算法依然能够正常工作。比如logistic就是这样的。
个参数,这样算法依然能够正常工作。比如logistic就是这样的。
在实际应用中,为了使算法看起来更直观更清楚,往往保留所有参数 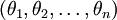 ,而不任意地将某一参数设置为 0。但此时需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
,而不任意地将某一参数设置为 0。但此时需要对代价函数做一个改动:加入权重衰减。权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。
目前对损失函数  的最小化还没有封闭解(closed-form),因此使用迭代的方法求解,如(Gradient Descent或者L-BFGS),经过求导,得到的梯度公式:
的最小化还没有封闭解(closed-form),因此使用迭代的方法求解,如(Gradient Descent或者L-BFGS),经过求导,得到的梯度公式:
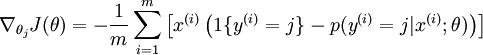
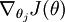 本身是一个向量,它的第
本身是一个向量,它的第  个元素
个元素 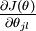 是
是  对
对 的第
的第  个分量的偏导数。在梯度下降法的标准实现中,每一次迭代需要进行如下更新:
个分量的偏导数。在梯度下降法的标准实现中,每一次迭代需要进行如下更新: 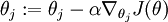 (
(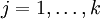 )。(
)。(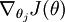 为方向,a代表在这个方向的步长)
为方向,a代表在这个方向的步长)
由于参数数量的庞大,所以可能需要权重衰减项来防止过拟合,一般的算法中都会有该项。添加一个权重衰减项 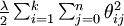 来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
来修改代价函数,这个衰减项会惩罚过大的参数值,现在我们的代价函数变为:
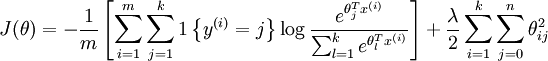
有了这个权重衰减项以后 (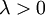 ),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为
),代价函数就变成了严格的凸函数,这样就可以保证得到唯一的解了。 此时的 Hessian矩阵变为可逆矩阵,并且因为 是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
是凸函数,梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。
为了使用优化算法,我们需要求得这个新函数  的导数,如下:
的导数,如下:
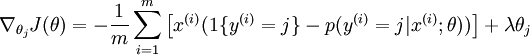
通过最小化  ,我们就能实现一个可用的 softmax 回归模型。
,我们就能实现一个可用的 softmax 回归模型。
最后一个问题在logistic的文章里提到过,关于分类器选择的问题,是使用logistic建立k个分类器呢,还是直接使用softmax回归,这取决于数据之间是否是互斥的,k-logistic算法可以解决互斥问题,而softmax不可以解决,比如将图像分到三个不同类别中。(i) 假设这三个类别分别是:室内场景、户外城区场景、户外荒野场景。 (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片
考虑到处理的问题的不同,在第一个例子中,三个类别是互斥的,因此更适于选择softmax回归分类器 。而在第二个例子中,建立三个独立的 logistic回归分类器更加合适。最后补一张k-logistic的图片:

(六)6.9 Neurons Networks softmax regression的更多相关文章
- CS229 6.9 Neurons Networks softmax regression
SoftMax回归模型,是logistic回归在多分类问题的推广,即现在logistic回归数据中的标签y不止有0-1两个值,而是可以取k个值,softmax回归对诸如MNIST手写识别库等分类很有用 ...
- (六) 6.1 Neurons Networks Representation
面对复杂的非线性可分的样本是,使用浅层分类器如Logistic等需要对样本进行复杂的映射,使得样本在映射后的空间是线性可分的,但在原始空间,分类边界可能是复杂的曲线.比如下图的样本只是在2维情形下的示 ...
- (六) 6.2 Neurons Networks Backpropagation Algorithm
今天得主题是BP算法.大规模的神经网络可以使用batch gradient descent算法求解,也可以使用 stochastic gradient descent 算法,求解的关键问题在于求得每层 ...
- (六) 6.3 Neurons Networks Gradient Checking
BP算法很难调试,一般情况下会隐隐存在一些小问题,比如(off-by-one error),即只有部分层的权重得到训练,或者忘记计算bais unit,这虽然会得到一个正确的结果,但效果差于准确BP得 ...
- (六)6.10 Neurons Networks implements of softmax regression
softmax可以看做只有输入和输出的Neurons Networks,如下图: 其参数数量为k*(n+1) ,但在本实现中没有加入截距项,所以参数为k*n的矩阵. 对损失函数J(θ)的形式有: 算法 ...
- CS229 6.10 Neurons Networks implements of softmax regression
softmax可以看做只有输入和输出的Neurons Networks,如下图: 其参数数量为k*(n+1) ,但在本实现中没有加入截距项,所以参数为k*n的矩阵. 对损失函数J(θ)的形式有: 算法 ...
- (六)6.13 Neurons Networks Implements of stack autoencoder
对于加深网络层数带来的问题,(gradient diffuse 局部最优等)可以使用逐层预训练(pre-training)的方法来避免 Stack-Autoencoder是一种逐层贪婪(Greedy ...
- (六)6.11 Neurons Networks implements of self-taught learning
在machine learning领域,更多的数据往往强于更优秀的算法,然而现实中的情况是一般人无法获取大量的已标注数据,这时候可以通过无监督方法获取大量的未标注数据,自学习( self-taught ...
- TensorFlow实战之Softmax Regression识别手写数字
关于本文说明,本人原博客地址位于http://blog.csdn.net/qq_37608890,本文来自笔者于2018年02月21日 23:10:04所撰写内容(http://blog.c ...
随机推荐
- iOS多线程的初步研究(三)-- NSRunLoop
弄清楚NSRunLoop确实需要花时间,这个类的概念和模式似乎是Apple的平台独有(iOS+MacOSX),很难彻底搞懂(iOS没开源,呜呜). 官网的解释是说run loop可以用于处理异步事件, ...
- 深入浅出ES6(八):Symbols
作者 Jason Orendorff github主页 https://github.com/jorendorff 你是否知道ES6中的Symbols是什么,它有什么作用呢?我相信你很可能不知道, ...
- editplus的各式插件
C/C++, Java, JSP, C#, .NET, SQL, Pascal, Python, Assembly, Basic files http://www.editplus.com/javac ...
- nodejs的require模块及路径
在nodejs中,模块大概可以分为核心模块和文件模块. 核心模块是被编译成二进制代码,引用的时候只需require表示符即可,如(require('net')). 文件模块,则是指js文件.json文 ...
- 李洪强iOS开发之计算数组的最大最小值
// // ViewController.m // A21 - 李洪强 - 输出参数 // // Created by vic fan on 16/7/3. // Copyright © 20 ...
- Linux问题定位工具大放送
我们在程序定位问题时,经常不知所错,但是在linux有很多强大的工具,只要我们合理利用,一定见奇效. 主要会遇到以下问题: 1 mem高 2 cpu高 3 io高 4 网络延迟高 vargrind:h ...
- Hibernate笔记——关联关系配置(一对多、一对一和多对多)
原文:http://www.cnblogs.com/otomedaybreak/archive/2012/01/20/2327695.html ============================ ...
- 【重走Android之路】【Java面向对象基础(一)】数据类型与运算符
[重走Android之路][基础篇(一)][Java面向对象基础]数据类型与运算符 1.数据类型介绍 在Java中,数据类型分为两种:基本数据类型和引用类型. 基本数据类型共8种,见下表: 基本数 ...
- linux驱动分离分层的概念
这个分离分层的概念和输入子系统有点像,但不是完全一样的.为什么会再弄一个这个模型出来我也没有搞懂,现在我的学习还停留在把知识学懂的层面上.至于为什么会产生这种知识,现在我还无从解释,还需时日成长. 这 ...
- Angular service
<!DOCTYPE html> <html lang="en" ng-app="myApp"> <head> <met ...
