Foundations of Machine Learning: The PAC Learning Framework(1)

写在最前：本系列主要是在阅读 Mehryar Mohri 等的最新书籍《Foundations of Machine Learning》以及 Schapire 和 Freund 的 《Boosting: Foundations and Algorithms》过程中所做的笔记。主要讨论三个部分的内容。第一部分是PAC的基本概念,介绍了泛化误差和经验误差，并且讨论了假设集$H$有限时的泛化边界。第二部分介绍了假设集$H$无限时的泛化边界，引入了三种衡量$H$复杂程度的机制，分别是Rademacher Complexity，Growth Function和VC-dimension。其中，Rademacher Complexity通过衡量对随机噪声的拟合好坏来评估一个函数族的复杂程度；但它在计算上是个NP问题。Growth Function则通过对任意$m$个点的样本划分结果所实现的总次数来衡量，由于$m$的任意性，它仍然是很难计算的。VC-dimension则是通过打散这一概念来衡量。第三部分介绍了Boosting方法。通过组合弱学习器，Boosting以很高的概率获得一个性能任意好的强学习器。我们具体介绍了AdaBoosting算法及其特性，并试图用之前建立的理论来分析AdaBoosting。

Foundations of Machine Learning: The PAC Learning Framework(1)

在计算学习理论，probably approximately correct learning(PAC learning)是分析机器学习的一个数学框架。这个框架解决了这样的一些问题：

1. 什么样的概念是能够被有效的学习出来？
2. 要达到一个成功的学习过程，至少要多少样本？

（一）PAC 学习模型。

（1）基本概念以及假设。

$\mathcal{X}:$输入空间（input space），所有可能的示例集合。
    $\mathcal{Y}:$输出空间（output space），所有可能的标签或者目标值的集合。当$\mathcal{Y}=\{0,1\}$时叫做二分类（binary classification）。
    概念（Concept） $c:\mathcal{X} \rightarrow \mathcal{Y}$，是从input space 到output space 的一个映射。
    概念集合(Concept Class) $C: $所有$c$的集合。
    假设集（Hypothesis  Set） $H:$所有假设$h$的集合。学习者会从这个集合中选出一个假设，做为最后的学习的结果。注意，这与前面的 Concept  class并不一定一致。
    一个假设：所有的样本是根据一个未知的分布$D$,以$iid$（独立同分布）的形式采样出来的。

有了上述的基本概念以及$iid$的假设后，我们可以如下描述一个学习的过程：
样本 $S=\{x_1,x_2,...,x_m\}$以$iid$形式根据分布$D$采样，基于某个特定的concept $ c \in C$,得到一组labels $ \{c(x_1),c(x_2),...,c(x_m)\}$。我们的任务就是根据训练集$\{(x_1,c(x_1)),...,(x_m,c(x_m))\}$,在Hypothesis  Set $H$里选择一个$h_s \in H$，使$h_s$最接近与concept $ c$。那么我们应该怎样去衡量“最接近”，以下定义两个衡量的标准。

（二）泛化错误以及经验错误。

定义 1.1 泛化错误(generalization error)：给定一个假设 $h \in H$，一个目标概念 $c \in C$，以及一个分布 $D$，那么 $h$ 的泛化错误定义为：

$$\mathcal{R}(h)= \mathop{Pr}_{x\backsim D}[h(x)\neq c(x)]=E_{x\backsim D}[\mathbb{I}(h(x)\neq c(x))]$$

这里的 $\mathbb{I}(w)$ 表示指示函数，当事件 $w$ 发生时其值为1，不发生时其值为0。

也就是说在分布$D$已知的情况下，用$h$去近视$c$会产生的真正错误。但通常这个分布$D$是未知的，所以上述泛化错误很难计算，所以用经验错误来估计上述错误。

定义 1.2 经验错误(empirical error)：给定一个假设 $h \in H$，一个目标概念 $c \in C$，以及一个样本 $S=\{x_1,x_2,...,x_m\}$，$h$ 的经验错误定义如下：

$$\widehat{\mathcal{R}}(h)=\frac{1}{m}\sum_{i=1}^{m}\mathbb{I}_(h(x)\neq c(x))$$

因此，empirical error 实际上是样本的平均错误，而 generalization error 是分布 $D$下的期望错误。并且二者有如下的关系：

\begin{eqnarray*}E[\widehat{\mathcal{R}}(h)] &=& E_{s\sim D^m}[\widehat{\mathcal{R}}(h)] \\&=& \frac{1}{m}\sum_{i=1}^{m}E_{s \backsim D^m}[\mathbb{I}(h(x_i \neq c(c_i)))]\\&=& \frac{1}{m}\sum_{i=1}^{m}E_{x\backsim D}[\mathbb{I}(h(x) \neq c(x))]\\&=& E_{x \backsim D}[\mathbb{I}(h(x) \neq c(x))] \\&=& \mathcal{R}(h)\end{eqnarray*}

（三）PAC-学习。

定义 1.3 PAC-学习（PAC-learning）：我们说一个概念集合 C 是PAC可学习的，当且仅当存在一个算法 $\mathcal{A}$ 以及一个多项式函数 $poly(\cdot,\cdot,\cdot,\cdot)$，使得对任意的 $\epsilon > 0$ 和 $\delta > 0$ 对所有在 $\mathcal{X}$ 上的分布 $D$，以及对所有的目标概念 $c \in C$，当样本大小$m$满足 $m\geq poly(1/\varepsilon,1/\delta,n,size(c))$ 时，以下不等式成立：

$$\mathop{Pr}_{S\sim D^m}[\mathcal{R}(h_S)\leq \varepsilon]\geq 1-\delta,$$

如果算法 $\mathcal{A}$ 的运行时间为 $poly(1/\varepsilon,1/\delta,n,size(c))$，那么我说概念集合 C 是有效的PAC可学习。当这样的算法存在时，我们把它叫做概念集合 C 的 PAC学习算法。

怎样去理解上述定义？对于一个$concept \ class \ C$，如果存在一个算法$\mathcal{A}$，在观察到一定数量的点后，返回一个假设$h$，并且这个假设$h$一很高的概率$(1-\delta)$保证$h$与$concept \ c$的接近度小于$\epsilon$，那么这个$concept \ class \ C$就是PAC-learnable。

关于PAC框架的定义，必须注意三点：

1. 它是一个distribution-free model，也就是说没有对分布作任何假设。
2. 测试样本和训练样本必须来自同分布。
3. PAC解决的是某一概念集C，而不是某个特定的概念。

  （四）例子：与坐标轴对齐的矩形。

我们来学习这样一个问题：输入空间为二维平面$R^2$，在这个二维平面上，只有某个与坐标轴对齐的矩阵内的点的label为+1，其他label为-1。我们来证明该问题是PAC-learnable。首先，把这个问题抽象成一个数学模型。其中，$\mathcal{A}=R^2,\mathcal{Y}=\{+1,-1\}$，概念集合 $C=\{$所有与坐标轴对齐的矩形内的点为+1$\}$，假设集 $H=\{$所有与坐标轴对齐的矩形内的点为+1$\}$。

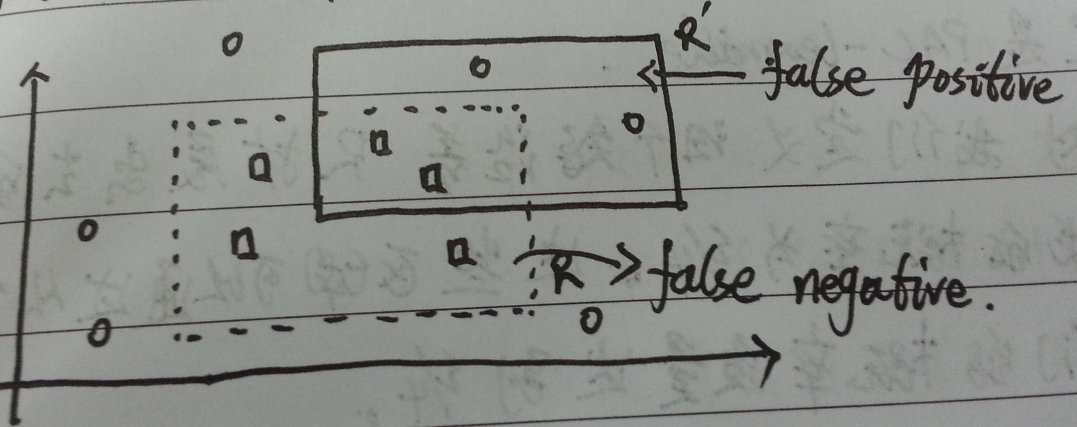
图一：目标概念 R 和可能的假设 R'

如图一所示，$R$（虚线框）代表一个特定的概念 $R\in C$，$R'$（实线框）代表假设$R' \in H$。其中：

1. false positive: 本来为-1的被假设$R'$标成+1，称为假阳性。
2. false negative: 本来为+1的被假设$R'$标成-1，称为假阴性。

为了证明上述$concept \ class$是$PAC-learnable$，即我们要证明存在某个算法$\mathcal{A}$使$PAC-learnable$的条件成立。现在我们构造这样一个算法$\mathcal{A}$：给定一个样本$S$，算法总是返回一个包括所有$+1$的最小矩形。即如图二，算法返回实线矩阵$R'$。可以看出这个算法不可能产生false positive，只可能在阴影部分产生false negative错误。

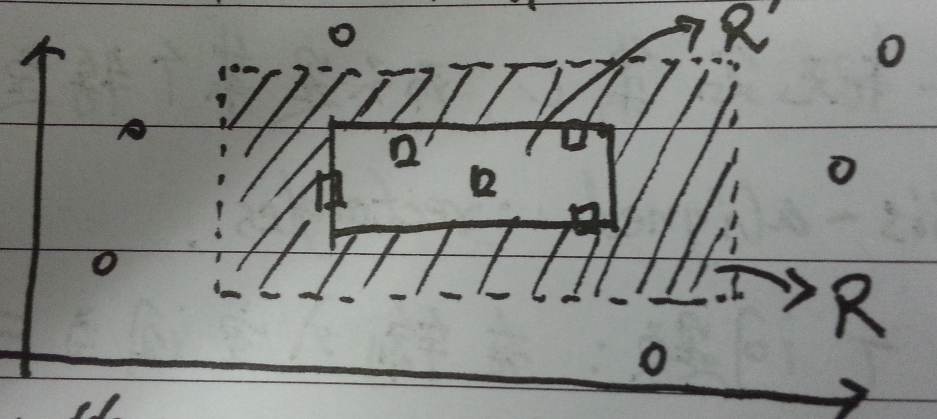
图二：算法$\mathcal{A}$的执行示例

现在我们来证明这个算法是PAC可学习的。令$R \in C$为目标$concept$。固定$\epsilon>0$.记$\mathop{Pr}[R]$为区域$R$所代表的概率质量，也就是基于分布$D$随机取一个点，落入区域$R$的概率。若$\mathop{Pr}[R] \leq \epsilon$，则$\mathop{Pr}[shaded \ area] \leq \mathop{Pr}[R] \leq \epsilon$，即$\mathcal{R}[R_s] \leq \epsilon$恒成立，故一定是PAC-learnable。

所以，我们假设 $\mathop{Pr}[R] > \epsilon$。我们定义沿着$R$扩展出去的矩阵区域为$r_1,r_2,r_3,r_4$，并且每个区域的概率为$\epsilon /4$。这些区域可以通过从空矩阵开始增长，直到它们的概率质量达到$\epsilon / 4$。如图三所示：

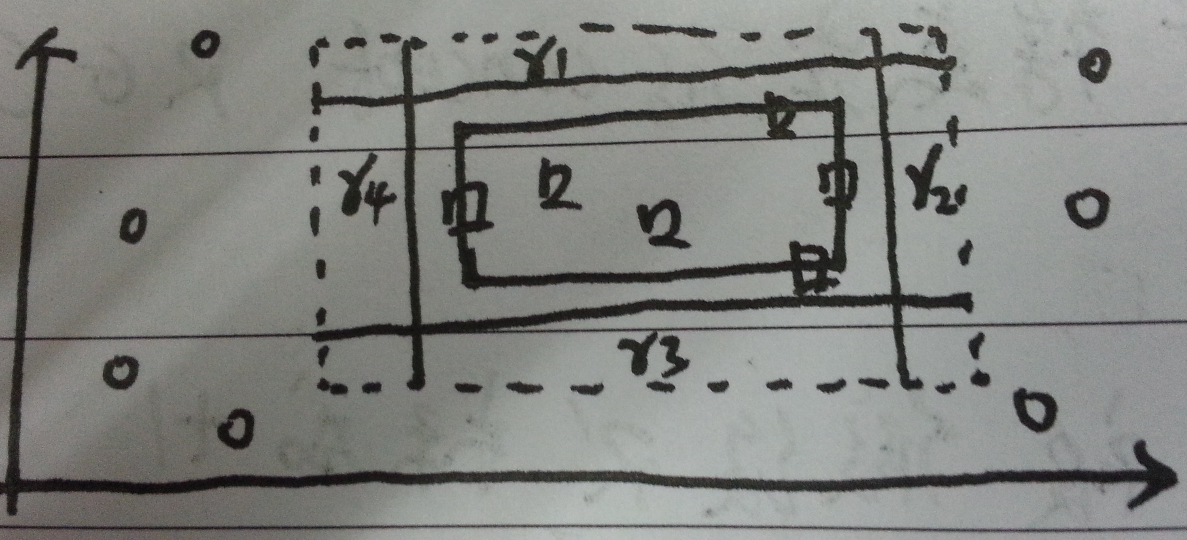
图三：四个沿着R扩展出去的矩阵

如果$R_s$与四个矩阵都相交的话，那么如图四所示可知:

\begin{align}\mathcal{R}[R_s] &= \mathop{Pr}[shaded \ area]&\leq \mathop{Pr}[r_1] + \mathop{Pr}[r_1] + \mathop{Pr}[r_3] + \mathop{Pr}[r_4]&= \epsilon\end{align}

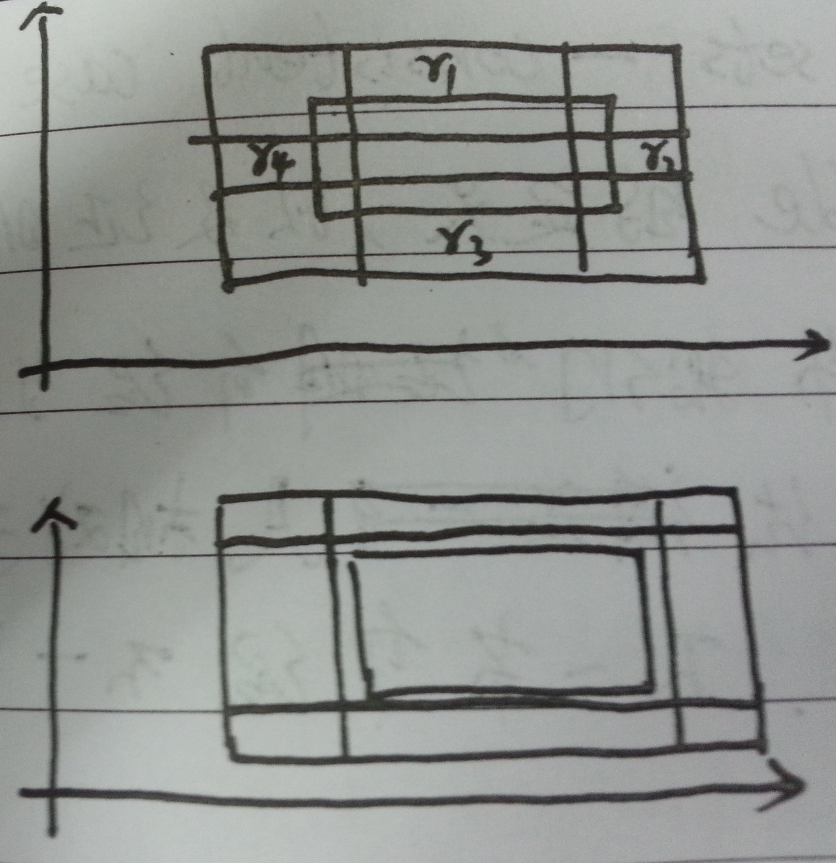
图四：四个矩阵与$R_s$都相交

相反，如果$\mathcal{R}[R_s] \leq \epsilon$,那么$R_s$就不一定会同时与$r_1,r_2,r_3,r_4$相交。如图四中下半图所示，重叠的部分可保证即使不与$R_s$相交也能使下式成立：

$$\mathop{Pr}[r_1]+\mathop{Pr}[r_2]+\mathop{Pr}[r_3]+\mathop{Pr}[r_4]=\epsilon$$

换句话说，从概率的角度来讲：

$$\mathop{Pr}_{s \backsim D^m}[\mathcal{R} \leq \epsilon] > \mathop{Pr}_{s \backsim D^m}[R_s \ intersect \ with \ r_1,r_2 ,r_3,r_4 \ at \ the \ same \ time]$$

它的逆否命题为：

\begin{eqnarray}& & \mathop{Pr}_{s \backsim D^m}[\mathcal{R}[R_s] > \epsilon] \nonumber\\&\leq& 1 - \mathop{Pr}_{s\backsim D^m}[R_s \ intersect \ with \ r_1,r_2 ,r_3,r_4 \ at \ the \ same \ time]\nonumber\\ &=& \mathop{Pr}_{s\backsim D^m}[R_s \ non-intersect \ with \ r_1,r_2,r_3,r_4 \ at \ least \ one]\nonumber\\ &=& \mathop{Pr}_{s\backsim D^m}[\bigcup_{i=1}^{4}\{R_s\bigcap r_i=\varnothing\}] \ \ \ \ \ \ (Use \ Union \ Bound)\nonumber\\ &\leq& \sum_{i=1}^{4}\mathop{Pr}_{s\backsim D^m}[\{R_s \bigcap r_i = \varnothing\}]\\ &\leq& 4(1-\epsilon/4)^m\label{equ:1}\\ &\leq& 4exp(-m\epsilon/4)\end{eqnarray}

不等式\ref{equ:1}成立是因为，假如$R_s\bigcap r_i\neq\varnothing$，那么根据算法$\mathcal{A}$产生$R_s$的方法在$R_s\bigcap r_i$中必定有一个lable为+1的点，要使$R_s\bigcap r_i=\varnothing$那么所有的点至少应该不落入$r_i$区域内，即概率为$(1-\epsilon/4)^m$。现在可以得到，若要使$\mathop{Pr}_{s\backsim D^m}[\mathcal{R}[R_s]>\epsilon] \leq \delta$，则必有

$$4exp(-m\epsilon/4)\leq \delta \Longleftrightarrow m \geq \frac{4}{\epsilon}log\frac{4}{\delta}$$

即当$m\geq \frac{4}{\epsilon}log\frac{4}{\delta}$时，$\mathop{Pr}_{s\backsim D^m}[\mathcal{R}[R_s] > \epsilon] \leq \delta$成立。证明结束。

思考问题：将算法$\mathcal{A}$换成返回最大的不包括负label的圆形，是否可以证明它是PAC-learnable？