深入理解KS

一、概述

KS（Kolmogorov-Smirnov）评价指标，通过衡量好坏样本累计分布之间的差值，来评估模型的风险区分能力。

KS、AUC、PR曲线对比：

1）ks和AUC一样，都是利用TPR、FPR两个指标来评价模型的整体训练效果。

2）不同之处在于，ks取的是TPR和FPR差值的最大值，能够找到一个最优的阈值；AUC只评价了模型的整体训练效果，并没有指出如何划分类别让预估的效果达到最好，就是没有找到好的切分阈值。

3）与PR曲线相比，AUC和KS受样本不均衡的影响较小，而PR受其影响较大。（详看P-R曲线及与ROC曲线区别）

KS的曲线图走势大概如下：

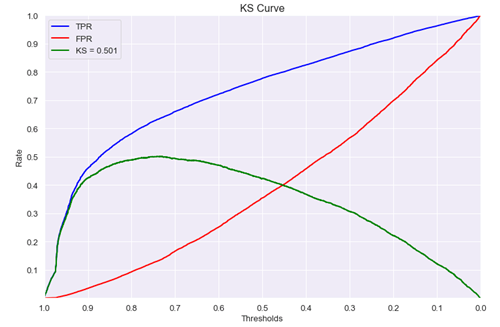
ks值<0.2,一般认为模型没有区分能力。

ks值[0.2,0.3],模型具有一定区分能力，勉强可以接受

ks值[0.3,0.5],模型具有较强的区分能力。

ks值大于0.75，往往表示模型有异常。

二、直观理解KS

1）如何直观的理解ks呢？

参考上述ks曲线图，可以这样理解，随着阈值从大逐渐的变小，TPR的提升速度高于FPR的提升速度，直到一个临界阈值threshold，之后TPR提升速度低于FPR，这个临界threshold便是最佳阈值。在前期TPR越快提升，模型效果越好；反之，FPR越快提升，模型效果就越差。

2）公式推导KS

前提假设：正负样本在当前模型下的预测值分布，都服从高斯分布。

令：

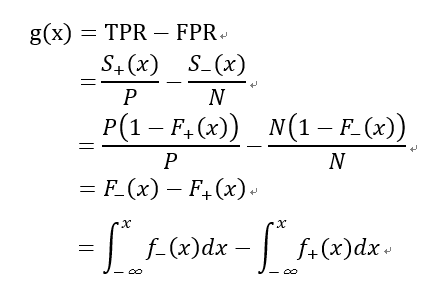
根据上述ks曲线图，可知ks曲线是一个凹函数，存在极大值，所以对g(x)求导，令其导数为0：

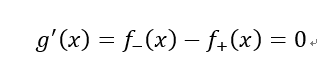
由此可知，当f_-(x)=f₊(x)的时候，g(x)取值最大，即为所求的KS值。

 注：

g(x)表示大于阈值x情况下的TPR-FPR的值,

s₊(x)表示大于阈值x情况下实际为正样本的个数

P表示正样本的总量

s_-(x)表示大于阈值x情况下实际为负样本的个数

N表示负样本的总量

F₊(x)表示在当前模型下实际正样本的概率分布函数，为什么要强调当前模型下，因为不同的模型对样本预测的值不一样，其概率分布也不一样。

F_-(x)表示在当前模型下实际负样本的概率分布函数

f₊(x)表示在当前模型下实际正样本的概率密度函数

f_-(x)表示在当前模型下实际负样本的概率密度函数

3)用概率密度函数直观展示KS值

从2）公式推导中我们发现，在当前模型预测下，正负样本的概率密度函数值相等时候，KS值最大。可以利用二元分类样本数据构建模型进行验证。

我们利用《西南财经大学新网银行杯数据科学竞赛》的数据进行验证，训练数据共15000条，筛选后有效特征122个，训练集、验证集、测试集按8:1:1切分，利用xgboost构建模型后对测试集进行打分，最终ks=0.52，最优阈值=0.0539，auc=0.82。将测试集的正负样本分开，根据其预测值分别画出对应的概率密度曲线，再画出x=0.0539直线，看最优阈值线是否与两个概率密度曲线的相交处也相交。如下图：

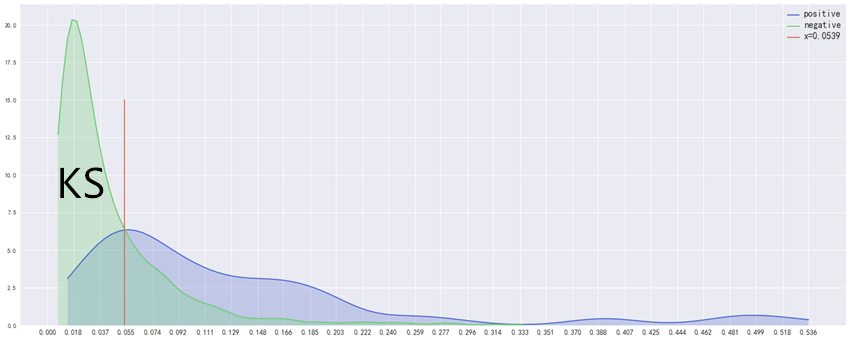
从2）中的g(x)我们知道，g(x)值等于在阈值x下，负样本<=x的概率减去正样本<=x的概率。

对应图中的概率密度曲线而言，就是在<=x条件下，绿色曲线下的面积减去蓝色去曲线下的面积。从图上也可以看出，两个分布交点处的阈值，是KS值最大对应的阈值，其KS值就等于红线左侧蓝线上方绿线下面的面积，阈值向左切或者往右切，所求面积都会变小。

红线就是我们所求的ks值最优阈值线，在图形上也与预期一致，三者相交于一点；从图中也看出ks值与正负样本比例无关系，只与模型对正负样本的预测值分布有关系。，但是如果样本量太小的话，其预测值的分布无法准确反应模型的性能，因此样本还是要达到一定数量。

另外，从正负样本预测值的概率密度函数，我们也能直观看出模型是否有效，如果模型比较有效，两个分布就会分的比较开，KS值自然比较大，所以这也是一种直观评测模型的方式。