51nod-1298 圆与三角形（计算几何超详解）

题目链接：http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1298

给出圆的圆心和半径，以及三角形的三个顶点，问圆同三角形是否相交。相交输出"Yes"，否则输出"No"。（三角形的面积大于0）。

 

Input第1行：一个数T，表示输入的测试数量(1 <= T <= 10000)，之后每4行用来描述一组测试数据。
4-1：三个数，前两个数为圆心的坐标xc, yc，第3个数为圆的半径R。(-3000 <= xc, yc <= 3000, 1 <= R <= 3000） 
4-2：2个数，三角形第1个点的坐标。 
4-3：2个数，三角形第2个点的坐标。 
4-4：2个数，三角形第3个点的坐标。(-3000 <= xi, yi <= 3000）Output共T行，对于每组输入数据，相交输出"Yes"，否则输出"No"。Sample Input

2
0 0 10
10 0
15 0
15 5
0 0 10
0 0
5 0
5 5

Sample Output

Yes
No

基础知识回顾：
点到直线距离公式：

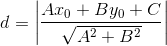
余弦定理：

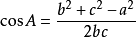
分析：

对于给定的三角形和圆，我们考虑相交的情况：

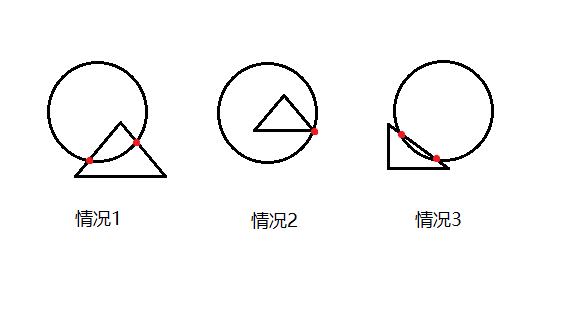
① 三角形有一点在圆内，有一点在圆外。

② 三角形有一点在圆上。

③三角形三点都在圆外，但有一条边与圆相交或相切。

前两种情况比较好写，只需要判断三角形三个端点到圆心的距离与半径的关系即可。

对于第三种情况，我们可以先判断圆心到三角形三条边的距离，如果有一条边到圆心的直线距离小于等于半径，我们进而去判断圆心到这条边所在直线的垂足是否在这条边上。如何去判断呢？

我们可以利用余弦定理，只要圆心与这条边的两个端点所成的角均为锐角（即cosα>0），那么垂足必然落在这条边上。

以下是AC代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
struct triangle//用结构体来存三角形三点的坐标
{
    double x[],y[];
};
double x,y,r;
triangle a;
//计算(x1,y1)与(x2,y2)之间的距离的平方
double point_dist(double x1,double y1,double x2,double y2)
{
    return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
//计算圆心(x,y)到直线Ax+By+C=0的距离的平方
double line_dist(double A,double B,double C)
{
    double ans = ( (A*x + B*y + C) * (A*x + B*y + C) ) / (A*A + B*B);
    return ans >  ? ans : -ans;
}
double f(double a,double b,double c)//余弦定理
{
    return (b + c - a) / (2.0 * sqrt(b * c));
}
int main()
{
    int i,j,t;
    cin>>t;
    while(t--)
    {
        //Input
        scanf("%lf%lf%lf",&x,&y,&r);
        for(i = ;i < ; i++)
        scanf("%lf%lf",&a.x[i],&a.y[i]);
        //Solve
        double dis1[],dis2[],dis3[];
        //dis1存放三角形三点到圆心距离的平方
        dis1[] = point_dist(x,y,a.x[],a.y[]);
        dis1[] = point_dist(x,y,a.x[],a.y[]);
        dis1[] = point_dist(x,y,a.x[],a.y[]);
        //dis2存放三角形三条边长的平方
        dis2[] = point_dist(a.x[],a.y[],a.x[],a.y[]);
        dis2[] = point_dist(a.x[],a.y[],a.x[],a.y[]);
        dis2[] = point_dist(a.x[],a.y[],a.x[],a.y[]);
        //dis3存放三角形三条边到圆心的直线距离的平方
        dis3[] = line_dist(a.y[]-a.y[],a.x[]-a.x[],(a.x[]-a.x[])*a.y[]+(a.y[]-a.y[])*a.x[]);
        dis3[] = line_dist(a.y[]-a.y[],a.x[]-a.x[],(a.x[]-a.x[])*a.y[]+(a.y[]-a.y[])*a.x[]);
        dis3[] = line_dist(a.y[]-a.y[],a.x[]-a.x[],(a.x[]-a.x[])*a.y[]+(a.y[]-a.y[])*a.x[]);
        double t1,t2;
        t1 = min(dis1[],min(dis1[],dis1[]));//t1为三点到圆心距离最小的那个
        t2 = max(dis1[],max(dis1[],dis1[]));//t2为三点到圆心距离最大的那个
        if(t1 <= r*r &&t2 >= r*r)//一点在圆内，一点在圆外或有一点在圆上
        cout<<"Yes"<<endl;
        else if(t1 > r*r)//三点都在圆外
        {
            if(dis3[] <= r*r)//dis3[0]是由点1和点2连接起来的边到圆心的距离
            {
                if(f(dis1[],dis2[],dis1[]) >  && f(dis1[],dis2[],dis1[]) > )
                {
                    cout<<"Yes"<<endl;
                    continue;
                }
            }
            if(dis3[] <= r*r)//dis3[1]是由点2和点3连接起来的边到圆心的距离
            {
                if(f(dis1[],dis2[],dis1[]) >  && f(dis1[],dis2[],dis1[]) > )
                {
                    cout<<"Yes"<<endl;
                    continue;
                }
            }
            if(dis3[] <= r*r)//dis3[2]是由点1和点2连接起来的边到圆心的距离
            {
                if(f(dis1[],dis2[],dis1[]) >  && f(dis1[],dis2[],dis1[]) > )
                {
                    cout<<"Yes"<<endl;
                    continue;
                }
            }
            cout<<"No"<<endl;
        }
        else
        cout<<"No"<<endl;
    }
    return ;
}

代码需注意的几点：

① 计算距离时不要用sqrt函数，会导致计算误差WA

② 已知三角形一条边的两端点(x1,y1)和(x2,y2)，我们将这条边的直线方程斜截式y=kx+b转换为一般式ax+by+c=0所得结果为 (y1-y2)x+(x2-x1)y+(x1-x2)y1+(y2-y1)x1=0,这也是给dis3数组赋值的依据。