bzoj 4332 FFT型的快速幂（需要强有力的推导公式能力）

 有n个小朋友，m颗糖，你要把所有糖果分给这些小朋友。

规则第 i 个小朋友没有糖果，那么他之后的小朋友都没有糖果。、
如果一个小朋友分到了 xx 个糖果，那么的他的权值是 f(x) = ox^2 + sx + u

没有分到糖果的小朋友的权值是 1

每种方案的权值是各个小朋友权值的乘积

求出所有方案的权值和

 

设g(i,j)表示前i个小朋友分j个糖果的权值乘积和

很容易得到一个式子

这个显然是一个卷积用FFT就可以处理

但是问题来了 我们如何得到ans呢

　　

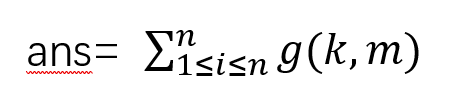
n<=1e8  朴素的算法不太行

要想办法优化一下

然后我就被卡死了  去看了网上的各种题解

顺便拔下来了一个封装性很好的FFT板子

看推导过程的点这个   想要迅速理解的看这个

然后你就看的懂下面这个式子了

然后就可以套快速幂了

 #include <cstdio>
 #include <cstring>
 #include <queue>
 #include <cmath>
 #include <algorithm>
 #include <set>
 #include <iostream>
 #include <map>
 #include <stack>
 #include <string>
 #include <vector>
 #define  eps 1e-9
 #define  fi first
 #define  se second
 #define  rtl   rt<<1
 #define  rtr   rt<<1|1
 #define  bug         printf("******\n")
 #define  mem(a,b)    memset(a,b,sizeof(a))
 #define  name2str(x) #x
 #define  fuck(x)     cout<<#x" = "<<x<<endl
 #define  f(a)        a*a
 #define  sf(n)       scanf("%d", &n)
 #define  sff(a,b)    scanf("%d %d", &a, &b)
 #define  sfff(a,b,c) scanf("%d %d %d", &a, &b, &c)
 #define  sffff(a,b,c,d) scanf("%d %d %d %d", &a, &b, &c, &d)
 #define  pf          printf
 #define  FRE(i,a,b)  for(i = a; i <= b; i++)
 #define  FREE(i,a,b) for(i = a; i >= b; i--)
 #define  FRL(i,a,b)  for(i = a; i < b; i++)+
 #define  FRLL(i,a,b) for(i = a; i > b; i--)
 #define  FIN         freopen("data.txt","r",stdin)
 #define  gcd(a,b)    __gcd(a,b)
 #define  lowbit(x)   x&-x
 #define rep(i,a,b) for(int i=a;i<b;++i)
 #define per(i,a,b) for(int i=a-1;i>=b;--i)
 using namespace std;
 typedef long long  LL;
 typedef unsigned long long ULL;
 int modu;
 namespace FFT {
 const double pi = acos ( -1.0 );
 struct cpx {
     double a, b;
     cpx ( double a = , double b =  ) : a ( a ), b ( b ) {}
     inline void init() {
         a = , b = ;
     }
     inline cpx operator + ( const cpx &ano ) const {
         return cpx ( a + ano.a, b + ano.b );
     }
     inline cpx operator - ( const cpx &ano ) const {
         return cpx ( a - ano.a, b - ano.b );
     }
     inline cpx operator * ( const cpx &ano ) const {
         return cpx ( a * ano.a - b * ano.b, b * ano.a + a * ano.b );
     }
 };
 typedef cpx C;
 typedef vector<C> vc;
 typedef vector<int> vi;

 vc a, b;

 void DFT ( vc &a, int oper =  ) {
     int n = a.size();
     for ( int i = , j = ; i < n; ++i ) {
         if ( i > j ) swap ( a[i], a[j] );
         for ( int l = n >> ; ( j ^= l ) < l; l >>=  );
     }
     for ( int l = , ll = ; l < n; l <<= , ll <<=  ) {
         double x = oper * pi / l;
         C omega = , omegan ( cos ( x ), sin ( x ) );
         for ( int k = ; k < l; ++k, omega = omega * omegan ) {
             for ( int st = k; st < n; st += ll ) {
                 C tmp = omega * a[st + l];
                 a[st + l] = a[st] - tmp;
                 a[st] = a[st] + tmp;
             }
         }
     }
     if ( oper == - ) for ( int i = ; i < n; ++i ) a[i].a /= n;
 }

 vi& operator * ( const vi &v1, const vi &v2 ) {
     int s = , ss = ( int ) v1.size() + ( int ) v2.size();
     while ( s < ss ) s <<= ;
     a.resize ( s ), b.resize ( s );
     for ( int i = ; i < s; ++i ) a[i].init(), b[i].init();
     for (  int i = ; i < v1.size(); ++i ) a[i] = v1[i];
     for (  int i = ; i < v2.size(); ++i ) b[i] = v2[i];
     DFT ( a ), DFT ( b );
     for ( int i = ; i < s; ++i ) a[i] = a[i] * b[i];
     DFT ( a, - );
     static vi res;
     res.resize ( v1.size() );
     for (  int i = ; i < v1.size(); ++i ) res[i] = ( a[i].a + 0.5 ), res[i] %= modu ;
     return res;
 }

 void operator *= ( vi &v1, const vi &v2 ) {
     int s = , ss = ( int ) v1.size() + ( int ) v2.size();
     while ( s < ss ) s <<= ;
     a.resize ( s ), b.resize ( s );
     for ( int i = ; i < s; ++i ) a[i].init(), b[i].init();
     for (  int i = ; i < v1.size(); ++i ) a[i] = v1[i];
     for (  int i = ; i < v2.size(); ++i ) b[i] = v2[i];
     DFT ( a ), DFT ( b );
     for ( int i = ; i < s; ++i ) a[i] = a[i] * b[i];
     DFT ( a, - );
     for (  int i = ; i < v1.size(); ++i ) v1[i] =  ( a[i].a + 0.5 ), v1[i] %= modu ;
 }

 void operator += ( vi &v1, const vi &v2 ) {
     for (  int i = ; i < v1.size(); ++i ) v1[i] = ( v1[i] + v2[i] + modu ) % modu;
 }
 }

 using namespace FFT;
 int m, p, n, o, s, u;
 vi f;
 vi expmod ( const vi&v, int b ) {
     vi res ( v.size(),  ), tmp = v;
     res[] = ;
     while ( b ) {
         if ( b &  ) res *= tmp;
         tmp *= tmp;
         b = b >> ;
     }
     return res;
 }
 vi& solve ( int n ) {
     static vi res, ghalf;
     if ( n ==  ) return res = ghalf = f;
     solve ( n /  );
     res += res * ghalf;
     ghalf *= ghalf;
     if ( n &  ) res += expmod ( f, n ), ghalf *= f;
     return res;
 }
 int main() {
     //FIN;
     sff ( m, modu );
     sffff ( n, o, s, u );
     f = vi ( m + ,  );
     for ( int i =  ; i < m +  ; i++ ) f[i] = ( 1LL * o * i * i + s * i + u ) % modu;
     vi &res = solve ( min ( n, m ) );
     printf ( "%d\n", res[m] );
     return ;
 }