「UVA557」 Burger（概率

本题征求翻译。如果你能提供翻译或者题意简述，请 提交翻译 ，感谢你的贡献。

题目描述

PDF

输入输出格式

输入格式：

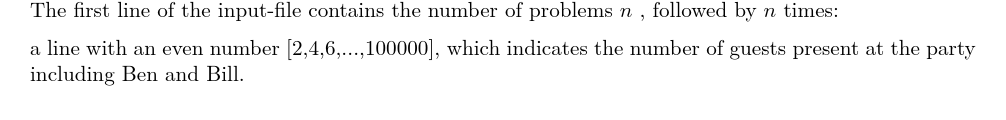
输出格式：

输入输出样例

输入样例#1： 复制

3
6
10
256

输出样例#1： 复制

0.6250
0.7266
0.9500

题解

这个本来是黄题被我打了个绿之后就变成绿题了哈哈哈哈哈哈哈

为了方便想我们设一共有$2n$个人，每种汉堡有$n$个。

>以下错解

>那么前$2n-2$个人中间必须要恰好有$n$个人选了一种汉堡，$n-2$个人选了另一种汉堡。

>那么就很好写啦，$ans=C_{2n-2}^{n}/2^{2n-2}$！

>然后发现n=3的样例都过不了qwq

>然后我跟队友YY分析出了原因：

>如果到第$i$个人的时候已经选了$n$个汉堡的话，那么它之后的选择概率就会从$\frac{1}{2}$变成$1$，这样直接把$2^{2n-2}$当方案数就会错掉qwq

怎么办呢？

考虑求后两个人能吃到不一样的汉堡的概率。

那么$now=C_{2n-2}^{n-1}/2^{2n-2}$！

这样我们只选到了$n-1$，就能保证每次选择的概率是$\frac{1}{2}$了qwq

最后容斥一下，$ans=1-now$就好了。

.

然后代码为了精度做了一些奇怪操作，总之就是求那个式子的就是了qwq

  qwerta
 UVA557 Burger Accepted
 代码 C++，.37KB
 提交时间 -- ::
 耗时/内存 2620ms, 0KB
 #include<iostream>
 #include<cstdio>
 using namespace std;
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         int n;
         scanf("%d",&n);
         n/=;
         double ans=;
         int tim=*n-;
         for(int i=;i<=n-;++i)
         {
             ans*=(i+n-);
             ans/=i;
             while(ans>=&&tim)
             {
                 ans*=0.5;
                 tim--;
             }
         }
         while(tim)
         {
             ans*=0.5;
             tim--;
         }
         printf("%.4f\n",-ans);
     }
     return ;
 }