动态规划专题 多阶段决策问题 蓝桥杯 K好数

问题描述

如果一个自然数N的K进制表示中任意的相邻的两位都不是相邻的数字，那么我们就说这个数是K好数。求L位K进制数中K好数的数目。例如K = 4，L = 2的时候，所有K好数为11、13、20、22、30、31、33 共7个。由于这个数目很大，请你输出它对1000000007取模后的值。

输入格式

输入包含两个正整数，K和L。

输出格式

输出一个整数，表示答案对1000000007取模后的值。

样例输入

4 2

样例输出

7

数据规模与约定

对于30%的数据，K^L <= 10⁶；

对于50%的数据，K <= 16， L <= 10；

对于100%的数据，1 <= K,L <= 100。

动态规划中多阶段决策问题的思想是每做一次决策（即一个阶段）就可以得到解的一部分，那么当所有的决策做完后，完整的解就出现了。

我们以此题为例，来看如何实现该问题的过程。

先简单将题意理解一下就是要求的整个数字串中每一个数字相邻的位置它们的数字不相邻的数字串的个数。

简单地来说，把题目的规模先减小，让自己好思考整个题目的思路。

比如如果长度是1，那么除了0之外的数字都可以填入。

如果长度为2呢，我这时必须知道两件事，第一它不相邻的数字有哪些（前一位），第二前一位某个数字以它为终点它所有的满足条件的总数。可以发现我要完成第二步是一定要用到第一步的。

即每个阶段由上一个阶段决定。

如果是长度3呢，当然也必须用到长度2的阶段的解。

我们用一个二维数组图来表示这样的过程。

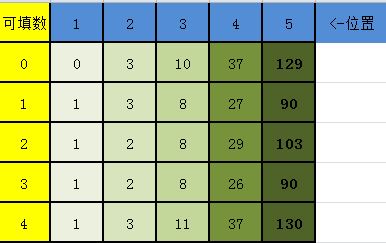
当然这题还有一个坑点，如果你想用上一阶段的SUM减去某几个不符合的值的话，很有可能出现由于值过大，已经取模的值减去两个很大的值而出现负数，这时最好的解决办法是全用循环加，不要出现减。

代码如下：

 #include<iostream>
 #include<cstdio>
 #define MAXN 105
 #define MOD %1000000007
 using namespace std;
 long long dp[MAXN][MAXN];
 int main()
 {
     long long i,j,k,c,l,sum=;
     cin>>k>>l;
     //初始化第一个格子
     dp[][]=;
     for(i=;i<k;i++)
         dp[i][]=;
     sum=k-;
     for(i=;i<=l;i++)
     {//格子
         for(j=;j<k;j++)
         {
             if(j==)
             {
                 dp[j][i]=(dp[j][i]+(dp[j][i-])MOD)MOD;
                 for(c=;c<k;c++)
                     dp[j][i]=(dp[j][i]+(dp[c][i-])MOD)MOD;　　//必须循环加，用sum减去一些值会负溢出！！
             }
             else if(j==k-)
             {
                 for(c=;c<k-;c++)
                     dp[j][i]=(dp[j][i]+(dp[c][i-])MOD)MOD;
                 dp[j][i]=(dp[j][i]+(dp[j][i-])MOD)MOD;
             }
             else
             {
                 for(c=;c<k;c++)
                 {
                     if(c!=j-&&c!=j+)
                         dp[j][i]=(dp[j][i]+(dp[c][i-])MOD)MOD;
                 }
             }
             //cout<<dp[j][i]<<" ";
          }
          sum=;
          for(j=;j<k;j++)
              sum=((sum)MOD+(dp[j][i])MOD)MOD;
         // cout<<endl;
         //cout<<sum<<endl;
     }
     cout<<sum<<endl;
     return ;
 }