poj 3070 && nyoj 148 矩阵快速幂

poj 3070 && nyoj 148 矩阵快速幂

题目链接

poj: http://poj.org/problem?id=3070

nyoj: http://acm.nyist.net/JudgeOnline/problem.php?pid=148

思路：

• 矩阵快速幂
• 直接求取
  
  

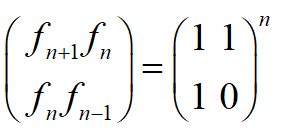
代码：

#include <iostream>
#include <string.h>
#include <math.h>
#include <stdio.h>
#include <algorithm>
using namespace std;
const int mod = 10000;
struct mat {
    int a[2][2];
    mat() {
        a[0][1]=a[1][0]=1;
        a[1][1]=a[0][0]=0;
    }
};
mat qpow(mat& x, mat& y) {
    mat z;
    z.a[0][1]=z.a[1][0]=0;
    for(int i=0;i<=1;++i) {
        for(int j=0;j<=1;++j) {
            for(int k=0;k<=1;++k) {
                z.a[i][j]=(z.a[i][j]%mod+(x.a[i][k]%mod*y.a[k][j])%mod)%mod;
            }
        }
    }
    return z;
}
int slove(int n) {
    mat x,res;
    res.a[0][1]=res.a[1][0]=0;
    res.a[1][1]=res.a[0][0]=1;
    x.a[0][0]=1;
    while(n) {
        if(n&1) res=qpow(res,x);//二进制分解
        x=qpow(x,x);
        n>>=1;
    }
    return res.a[0][1];
}
int main() {
    int n;
    while(~scanf("%d",&n)&&n!=-1) {
        printf("%d\n",slove(n));
    }
    return 0;
}