深入理解softmax函数

　　Softmax回归模型，该模型是logistic回归模型在多分类问题上的推广，在多分类问题中，类标签  可以取两个以上的值。Softmax模型可以用来给不同的对象分配概率。即使在之后，我们训练更加精细的模型时，最后一步也需要用softmax来分配概率。本质上其实是一种多种类型的线性分割，当类标签  取 2 时，就相当于是logistic回归模型。

　　在 softmax回归中，我们解决的是多分类问题（相对于 logistic 回归解决的二分类问题），类标  可以取  个不同的值（而不是 2 个）。因此，对于训练集 ，我们有 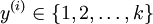。（注意此处的类别下标从 1 开始，而不是 0）。例如，在 MNIST 数字识别任务中，我们有  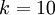个不同的类别。

　　对于给定的测试输入 ，我们想用假设函数针对每一个类别j估算出概率值 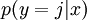。也就是说，我们想估计  的每一种分类结果出现的概率。因此，我们的假设函数将要输出一个  维的向量（向量元素的和为1）来表示这  个估计的概率值。 具体地说，我们的假设函数 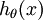 形式如下：

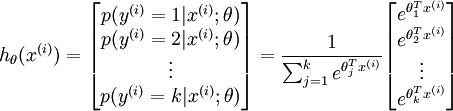
交叉熵代价函数

    

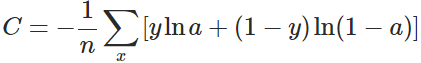
其中，x表示样本，n表示样本的总数。

这种代价函数与普通的二次代价函数相比，当预测值与实际值的误差越大，那么参数调整的幅度就更大，达到更快收敛的效果。

证明如下：

　 

其中：

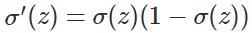
因此，w的梯度公式中原来的被消掉了；另外，该梯度公式中的表示输出值与实际值之间的误差。所以，当误差越大，梯度就越大，参数w调整得越快，训练速度也就越快。同理可得，b的梯度为：

Softmax 回归 vs. k 个二元分类器

如果你在开发一个音乐分类的应用，需要对k种类型的音乐进行识别，那么是选择使用 softmax 分类器呢，还是使用 logistic 回归算法建立 k 个独立的二元分类器呢？

这一选择取决于你的类别之间是否互斥，例如，如果你有四个类别的音乐，分别为：古典音乐、乡村音乐、摇滚乐和爵士乐，那么你可以假设每个训练样本只会被打上一个标签（即：一首歌只能属于这四种音乐类型的其中一种），此时你应该使用类别数 k = 4 的softmax回归。（如果在你的数据集中，有的歌曲不属于以上四类的其中任何一类，那么你可以添加一个“其他类”，并将类别数 k 设为5。）

如果你的四个类别如下：人声音乐、舞曲、影视原声、流行歌曲，那么这些类别之间并不是互斥的。例如：一首歌曲可以来源于影视原声，同时也包含人声 。这种情况下，使用4个二分类的 logistic 回归分类器更为合适。这样，对于每个新的音乐作品 ，我们的算法可以分别判断它是否属于各个类别。

现在我们来看一个计算视觉领域的例子，你的任务是将图像分到三个不同类别中。(i) 假设这三个类别分别是：室内场景、户外城区场景、户外荒野场景。你会使用sofmax回归还是 3个logistic 回归分类器呢？ (ii) 现在假设这三个类别分别是室内场景、黑白图片、包含人物的图片，你又会选择 softmax 回归还是多个 logistic 回归分类器呢？

在第一个例子中，三个类别是互斥的，因此更适于选择softmax回归分类器 。而在第二个例子中，建立三个独立的 logistic回归分类器更加合适。