2018-2019-2 《网络对抗技术》Exp0 Kali安装 Week1

kali下载：镜像文件通过同学获得

kali具体安装步骤：

  • 打开VMware，点击新建虚拟机，进行创建

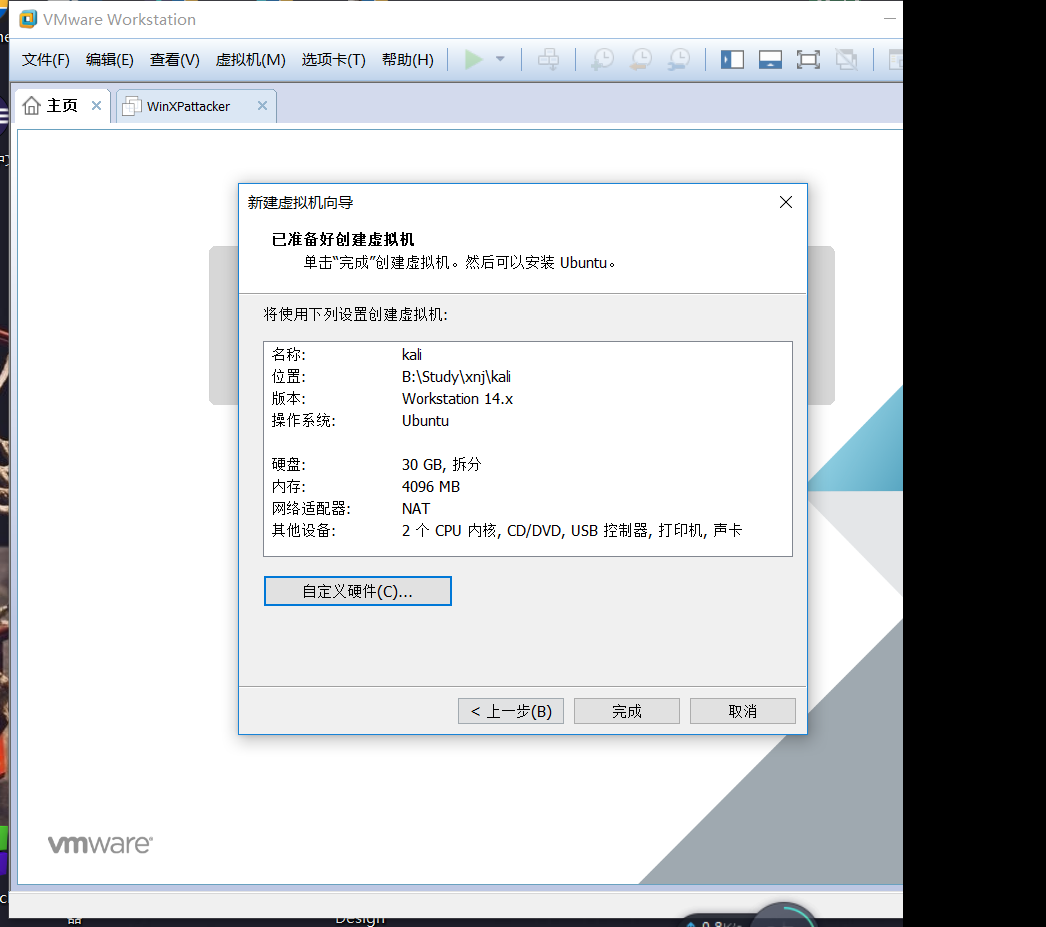
  • 创建完成后，启动kali虚拟机，进行设置

  • 主机名为我自己的名字

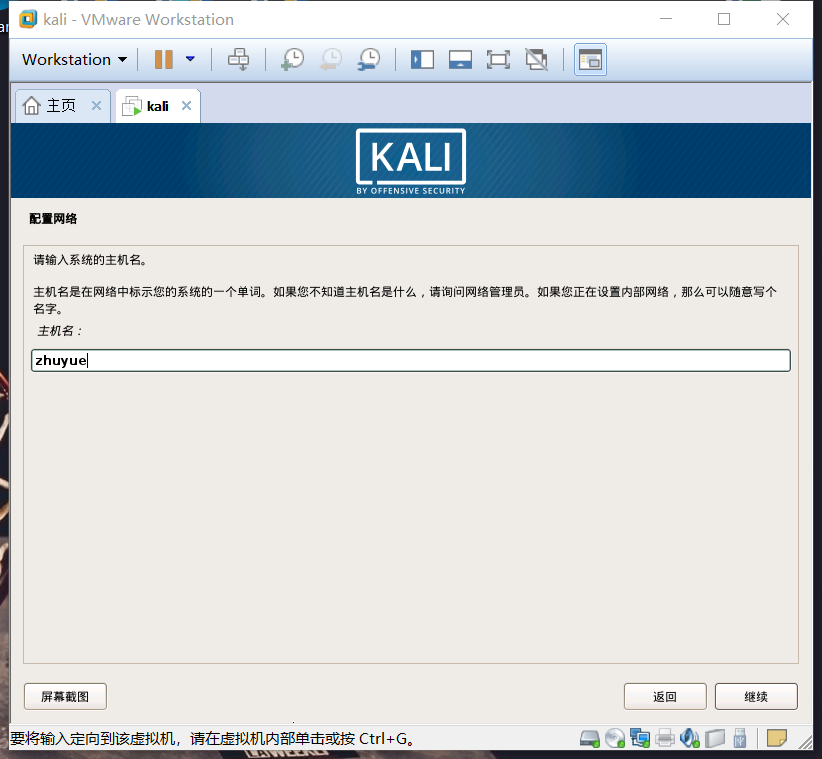
  • 继续安装

  • 安装成功后，重启虚拟机，输入用户名：root 和 之前设置的用户名密码

VMwareTools安装

  • 开始安装VMware Tools，在VM中点击“虚拟机”再点击“安装VMware tools”
  • 将 VMwareTools-10.1.15-6627299.tar.gz （根据压缩文件名而定）移动到主页面

  • 在主页面打开终端，使用 tar -zxvf VMwareTools-10.1.15-6627299.tar.gz 命令进行解压

  • 在解压文件夹中打开终端，使用./vmware-install.pl 进行安装

  • 安装完成

配置网络

  • 下载的镜像文件已经设置好了，无需再设置

配置共享文件夹

  • 点开“虚拟机”“设置”即可设置

  • 检查是否配置成功

参考：kali安装过程

20165227《网络对抗技术》Exp0 Kali安装 Week1的更多相关文章

  1. 2018-2019-2 《网络对抗技术》Kali安装 Week1 20165236

    2018-2019-2 <网络对抗技术>Kali安装 Week1 20165236 一.kali 下载 安装 网络 共享 软件源 二.安装步骤 1.官网上下载kali Linux: 2.参 ...

  2. 2018-2019-2 《网络对抗技术》Kali安装 Week1 20165212

    2018-2019-2 <网络对抗技术>Kali安装 Week1 20165212 1.完成安装linux kali和vm tools 装的第三遍成功安装.前面两次镜像文件不行,没驱动(网 ...

  3. 2018-2019 20165235 网络对抗技术 Exp0:kali的安装

    2018-2019 20165235 网络对抗技术 Exp0:kali的安装 安装kali 在官网上https://www.kali.org/下载kali 下载之后进行解压 打开VMware-> ...

  4. 20165309 《网络对抗技术》 Kali安装

    20165309 <网络对抗技术> Kali安装 1. 目的要求 下载 安装 网络 共享 软件源 2. 主要步骤 下载系统镜像文件 进入Kali官网下载,我选择的是64位版本: 虚拟机设置 ...

  5. 2018-2019-2 20165209 《网络对抗技术》 Kali安装

    2018-2019-2 20165209 <网络对抗技术> Kali安装 目录内容 下载 安装 网络 共享 软件源 下载kali kali下载官网地址 我下载的版本(如下图所示) 安装 打 ...

  6. 20165305 《网络对抗技术》 Kali安装

    一.安装kali 在虚拟机中安装kali我参考了下面的网页,里面写的很全面,所以我就不重复了,我主要说一下kali里面的环境配置. 在虚拟机中安装kali linux 注意:输入用户和密码时,kali ...

  7. 20165313 《网络对抗技术》 Kali安装

    一.目的要求 下载 安装 网络 共享 软件源 二.主要步骤 我主要是按照最新超详细虚拟机VMware安装Kali Linux 这个方法做的就没有步骤描述了. 安装结果图: 注意事项 安装过程中如果没有 ...

  8. 2019-2020-2 20174314王方正 《网络对抗》 Exp0 Kali安装

    本博旨记录安装Kali的具体步骤. 一.Vmware的安装 略. 二.Vmware的配置 选择[文件]-[新建虚拟机]. 出现新建虚拟机导向,按照以下图示配置每一步.

  9. 20165311 《网络对抗技术》 Kali安装

    一.目的要求 下载 安装 网络 共享 软件源 二.主要步骤 从官网下载软件安装包 安装的比较顺利 具体截图就不放上来了 安装结果图: 网络配置和共享文件夹设置 网络配置: 由于我之前安装虚拟机,所以并 ...

  10. 2018-2019-2 20165239 《网络对抗技术》Kali的安装 第一周

    2018-2019-<网络对抗技术> Kali安装 20165239其米仁增 一.资源下载以及工具安装 1.下载虚拟机工具VMware. 下载链接 :https://www.baidu.c ...

随机推荐

  1. BZOJ2662[BeiJing wc2012]冻结——分层图最短路

    题目描述 “我要成为魔法少女!”     “那么,以灵魂为代价,你希望得到什么?” “我要将有关魔法和奇迹的一切,封印于卡片之中„„”     在这个愿望被实现以后的世界里,人们享受着魔法卡片(Spe ...

  2. Dapper 连表查询

    实体类: UserInfo: public partial class UserInfo { public UserInfo() { this.Persion = new HashSet<Per ...

  3. Java中浮点型数据Float和Double进行精确计算的问题

    Java中浮点型数据Float和Double进行精确计算的问题 来源  https://www.cnblogs.com/banxian/p/3781130.html 一.浮点计算中发生精度丢失     ...

  4. MT【17】利用柯西不等式求三角的最大值

    评:此题也可以设$1+cos\theta=t$,平方后变成$t$的单变量利用均值去做. 柯西平衡系数法其实就是待定系数法,利用等号取到的条件.

  5. Hdoj 基本输入输出8道(1089-1096)

    Hdoj 1089 #include<bits/stdc++.h> using namespace std; int main() { int a,b; while(cin>> ...

  6. android 开启闪光灯小应用

    该程序需要在AndroidManifest.xml添加权限,属性 android:screenOrientation="portrait" android.permission.C ...

  7. suoi08 一收一行破 (tarjanLca+树状数组)

    用一个差分树状数组维护一下每个深度的和,然后每次拿着路径端点和lca加一加减一减就行了 #include<bits/stdc++.h> #define pa pair<int,int ...

  8. 【洛谷P2607】骑士 没有上司的舞会+

    题目大意:给定一个 N 个点的外向树森林,点有点权.从该树中选出若干顶点组成一个集合,满足任意相邻的两个顶点不同时出现在该集合中,求这样集合中点权和的最大值为多少. 题解:与树相比,该题多了环这个结构 ...

  9. MATLAB：图像滤波，绝对值差（filter2，imabsdiff函数）

    下面是对图像进行滤波,以及求滤波后的图像与原图像的绝对值差的实现过程,涉及到的函数有filter2,imabsdiff函数: close all; %关闭当前所有图形窗口,清空工作空间变量,清除工作空 ...

  10. 用webstorm来开发微信小程序之less的配置

    1.安装less. 安装好node之后,打开运行-->cmd-->进入安装node的文件夹目录-->输入 npm install -g less. 然后自动就会在C:\Users\A ...