KL距离，Kullback-Leibler Divergence

http://www.cnblogs.com/ywl925/p/3554502.html

http://www.cnblogs.com/hxsyl/p/4910218.html

http://blog.csdn.net/acdreamers/article/details/44657745

KL距离，是Kullback-Leibler差异（Kullback-Leibler Divergence）的简称，也叫做相对熵（Relative Entropy）。它衡量的是相同事件空间里的两个概率分布的差异情况。其物理意义是：在相同事件空间里，概率分布P(x)的事件空间，若用概率分布Q（x）编码时，平均每个基本事件（符号）编码长度增加了多少比特。我们用D（P||Q）表示KL距离，计算公式如下：

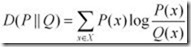
当两个概率分布完全相同时，即P(x)=Q(X)，其相对熵为0 。我们知道，概率分布P(X)的信息熵为：

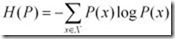
其表示，概率分布P(x)编码时，平均每个基本事件（符号）至少需要多少比特编码。通过信息熵的学习，我们知道不存在其他比按照本身概率分布更好的编码方式了，所以D(P||Q）始终大于等于0的。虽然KL被称为距离，但是其不满足距离定义的三个条件：1）非负性；2）对称性（不满足）；3）三角不等式（不满足）。

我们以一个例子来说明，KL距离的含义。

假如一个字符发射器，随机发出0和1两种字符，真实发出概率分布为A，但实际不知道A的具体分布。现在通过观察，得到概率分布B与C。各个分布的具体情况如下：

A(0)=1/2，A(1)=1/2

B(0)=1/4，B(1)=3/4

C(0)=1/8，C(1)=7/8

那么，我们可以计算出得到如下：

也即，这两种方式来进行编码，其结果都使得平均编码长度增加了。我们也可以看出，按照概率分布B进行编码，要比按照C进行编码，平均每个符号增加的比特数目少。从分布上也可以看出，实际上B要比C更接近实际分布。

如果实际分布为C，而我们用A分布来编码这个字符发射器的每个字符，那么同样我们可以得到如下：

再次，我们进一步验证了这样的结论：对一个信息源编码，按照其本身的概率分布进行编码，每个字符的平均比特数目最少。这就是信息熵的概念，衡量了信息源本身的不确定性。另外，可以看出KL距离不满足对称性，即D(P||Q)不一定等于D(Q||P)。

当然，我们也可以验证KL距离不满足三角不等式条件。

上面的三个概率分布，D(B||C)=1/4log2+3/4log(6/7)。可以得到：D(A||C) - (D(A||B)+ D(B||C)) =1/2log2+1/4log(7/6)>0，这里验证了KL距离不满足三角不等式条件。所以KL距离，并不是一种距离度量方式，虽然它有这样的学名。

其实，KL距离在信息检索领域，以及统计自然语言方面有重要的运用。我们将会把它留在以后的章节中介绍。

其他相关链接：http://en.wikipedia.org/wiki/Kullback-Leibler_divergence

http://hi.baidu.com/shdren09/item/e6441ec2bd495b0e0ad93aca

利用信息论的方法可以进行一些简单的自然语言处理

比如利用相对熵进行分类或者是利用相对熵来衡量两个随机分布的差距，当两个随机分布相同时，其相对熵为0.当两个随机分布的差别增加时，器相对熵也增加。我们下面的实验是为了横量概率分布的差异。

试验方法、要求和材料

要求：

1.任意摘录一段文字，统计这段文字中所有字符的相对频率。假设这些相对频率就是这些字符的概率（即用相对频率代替概率）；

2.另取一段文字，按同样方法计算字符分布概率；

3.计算两段文字中字符分布的KL距离；

4.举例说明（任意找两个分布p和q）,KL距离是不对称的，即D(p//q)!=D(q//p);

方法：

D（p//q）=sum(p(x)*log(p(x)/q(x)))。其中p(x)和q(x)为两个概率分布

约定 0*log(0/q(x))=0;p(x)*log(p(x)/0)=infinity;

具体实验可参考：http://www.cnblogs.com/finallyliuyu/archive/2010/03/12/1684015.html

相对熵（relative entropy）又称为KL散度（Kullback–Leibler divergence，简称KLD），信息散度（information divergence），信息增益（information gain）。 
　　KL散度是两个概率分布P和Q差别的非对称性的度量。

KL散度是用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的比特个数。 典型情况下，P表示数据的真实分布，Q表示数据的理论分布，模型分布，或P的近似分布。

　　根据shannon的信息论，给定一个字符集的概率分布，我们可以设计一种编码，使得表示该字符集组成的字符串平均需要的比特数最少。假设这个字符集是X，对x∈X，其出现概率为P(x)，那么其最优编码平均需要的比特数等于这个字符集的熵：

　　H(X)=∑_x∈XP(x)log[1/P(x)]

　　在同样的字符集上，假设存在另一个概率分布Q(X)。如果用概率分布P(X)的最优编码（即字符x的编码长度等于log[1/P(x)]），来为符合分布Q(X)的字符编码，那么表示这些字符就会比理想情况多用一些比特数。KL-divergence就是用来衡量这种情况下平均每个字符多用的比特数，因此可以用来衡量两个分布的距离。即：

　　D_KL(Q||P)=∑_x∈XQ(x)[log(1/P(x))] - ∑_x∈XQ(x)[log[1/Q(x)]]=∑_x∈XQ(x)log[Q(x)/P(x)]

　　由于-log(u)是凸函数，因此有下面的不等式

　　D_KL(Q||P) = -∑_x∈XQ(x)log[P(x)/Q(x)] = E[-logP(x)/Q(x)] ≥ -logE[P(x)/Q(x)] = -　　log∑_x∈XQ(x)P(x)/Q(x) = 0

　　即KL-divergence始终是大于等于0的。当且仅当两分布相同时，KL-divergence等于0。

　　===========================

　　举一个实际的例子吧：比如有四个类别，一个方法A得到四个类别的概率分别是0.1,0.2,0.3,0.4。另一种方法B（或者说是事实情况）是得到四个类别的概率分别是0.4,0.3,0.2,0.1,那么这两个分布的KL-Distance(A,B)=0.1*log(0.1/0.4)+0.2*log(0.2/0.3)+0.3*log(0.3/0.2)+0.4*log(0.4/0.1)

　　这个里面有正的，有负的，可以证明KL-Distance()>=0.

　　从上面可以看出， KL散度是不对称的。即KL-Distance(A,B)!=KL-Distance(B,A)

　　KL散度是不对称的，当然，如果希望把它变对称，

　　Ds(p1, p2) = [D(p1, p2) + D(p2, p1)] / 2.

二、第二种理解

　　今天开始来讲相对熵，我们知道信息熵反应了一个系统的有序化程度，一个系统越是有序，那么它的信息熵就越低，反之就越高。下面是熵的定义

　　如果一个随机变量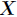的可能取值为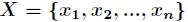，对应的概率为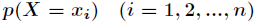，则随机变量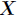的熵定义为

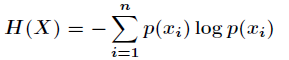
　　有了信息熵的定义，接下来开始学习相对熵。

　　1. 相对熵的认识

相对熵又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度（即KL散度）等。设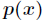和

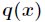
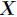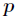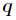是取值的两个概率概率分布，则对的相对熵为

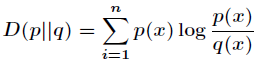
在一定程度上，熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是

用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q

表示数据的理论分布，模型分布，或P的近似分布。

2. 相对熵的性质

相对熵（KL散度）有两个主要的性质。如下

（1）尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即

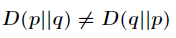
（2）相对熵的值为非负值，即

在证明之前，需要认识一个重要的不等式，叫做吉布斯不等式。内容如下

　　3. 相对熵的应用

相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增

大时，它们的相对熵也会增大。所以相对熵（KL散度）可以用于比较文本的相似度，先统计出词的频率，然后计算

KL散度就行了。另外，在多指标系统评估中，指标权重分配是一个重点和难点，通过相对熵可以处理。

三、用在CF中

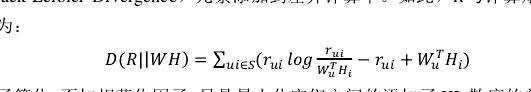
　　第一，KLD需要概率（脸颊和1），但是用评分。

　　第二，后面两项的作用。

今天开始来讲相对熵，我们知道信息熵反应了一个系统的有序化程度，一个系统越是有序，那么它的信息熵就越低，反

之就越高。下面是熵的定义

如果一个随机变量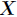的可能取值为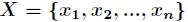，对应的概率为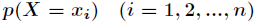，则随机变

量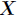的熵定义为

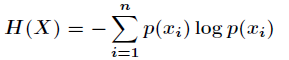
有了信息熵的定义，接下来开始学习相对熵。

Contents

   1. 相对熵的认识

   2. 相对熵的性质

   3. 相对熵的应用

1. 相对熵的认识

相对熵又称互熵，交叉熵，鉴别信息，Kullback熵，Kullback-Leible散度（即KL散度）等。设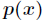和

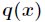
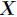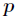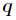是取值的两个概率概率分布，则对的相对熵为

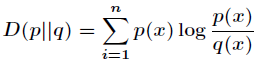
在一定程度上，熵可以度量两个随机变量的距离。KL散度是两个概率分布P和Q差别的非对称性的度量。KL散度是

用来度量使用基于Q的编码来编码来自P的样本平均所需的额外的位元数。 典型情况下，P表示数据的真实分布，Q

表示数据的理论分布，模型分布，或P的近似分布。

2. 相对熵的性质

相对熵（KL散度）有两个主要的性质。如下

（1）尽管KL散度从直观上是个度量或距离函数，但它并不是一个真正的度量或者距离，因为它不具有对称性，即

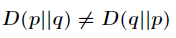
（2）相对熵的值为非负值，即

在证明之前，需要认识一个重要的不等式，叫做吉布斯不等式。内容如下

3. 相对熵的应用

相对熵可以衡量两个随机分布之间的距离，当两个随机分布相同时，它们的相对熵为零，当两个随机分布的差别增

大时，它们的相对熵也会增大。所以相对熵（KL散度）可以用于比较文本的相似度，先统计出词的频率，然后计算

KL散度就行了。另外，在多指标系统评估中，指标权重分配是一个重点和难点，通过相对熵可以处理。

在Julia中，有一个KLDivergence包，用来计算两个分布之间的K-L距离，它需要依赖Distributions包，用

法详见：https://github.com/johnmyleswhite/KLDivergence.jl