理顺FFT
DFT(Discrete Fourier Transform):离散傅立叶变换
直观的计算DFT算法复杂度为O(N*N)。
FFT(Fast Fourier Transformation):快速傅立叶变换,DFT的快速算法。凡将DFT算法复杂度降至O(N*logN)的算法,均可称为FFT。
最常用的FFT为奇偶分治法,要求输入点个数N为2的幂。下文中均假设N为2的幂。
N个点的DFT处理器定义:
N个点的DFT处理器有N个输入和N个输出,输入N个点的值,输出各点的变换结果值。
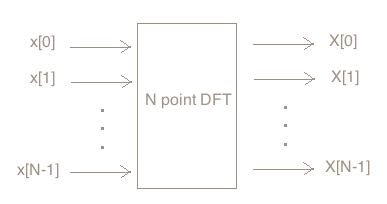 (注意左边x为小写,右边X为大写)
(注意左边x为小写,右边X为大写)
黑箱内逻辑为:
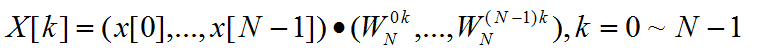
其中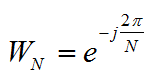 。
。
根据N个点的DFT处理器的定义,可以推得N/2个点的DFT处理器的定义。
N/2个点的DFT处理器定义:
N/2个点的DFT处理器有N/2个输入和N/2个输出,输入N/2个点的值,输出各点的变换结果值。

黑箱内逻辑为:
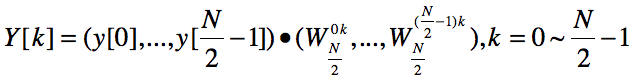
考虑下面问题:
问题一:将N/2个偶点x[0],x[2],x[4],...,x[N-2]输入N/2个点的DFT处理器,设输出为G[0],G[1],...,G[N/2-1],那么G[k](k=1~N/2-1)等于多少?
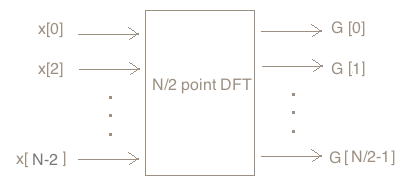
解:根据N/2个点的DFT处理器定义,得:
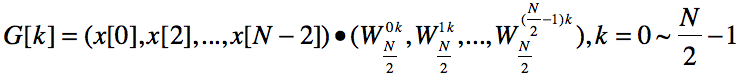
问题二:将N/2个奇点x[1],x[3],x[5],...,x[N-1]输入N/2个点的DFT处理器,设输出为H[0],H[1],...,H[N/2-1],那么H[k](k=1~N/2-1)等于多少?
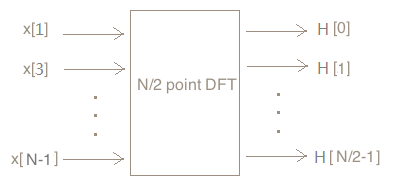
解:根据N/2个点的DFT处理器定义,得
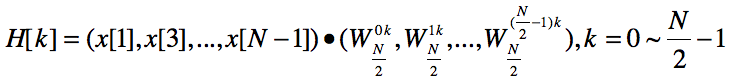
考虑下面问题:
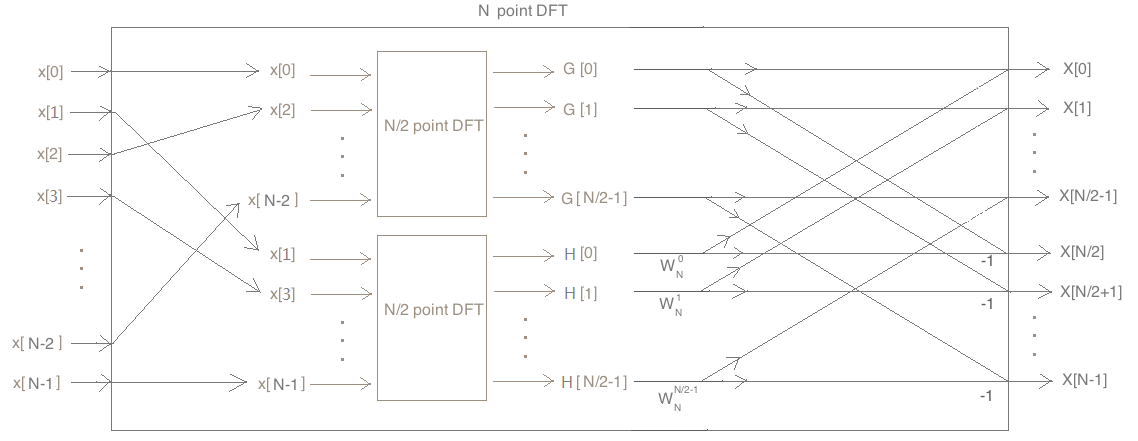
假设我现在想计算N个点x[0]~x[N-1]的DFT的结果X[0]~X[N-1],但是凑巧学前班没毕业不会算数儿,所以只能借助一个现成的N个点的DFT处理器来完成计算,但凑巧手头没有N个点的DFT处理器,却凑巧有两个N/2个点的DFT处理器,那么我还能不能完成计算呢?
解:
能完成计算,可以用两个N/2个点的DFT处理器DIY一个N个点的DFT处理器,然后用这个DIY的DFT处理器完成计算。
那么,如何DIY呢?
首先可验证恒等式:
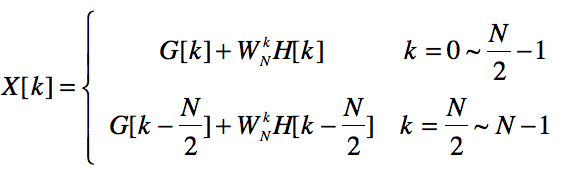
然后据此恒等式连电路,连好结果如下:
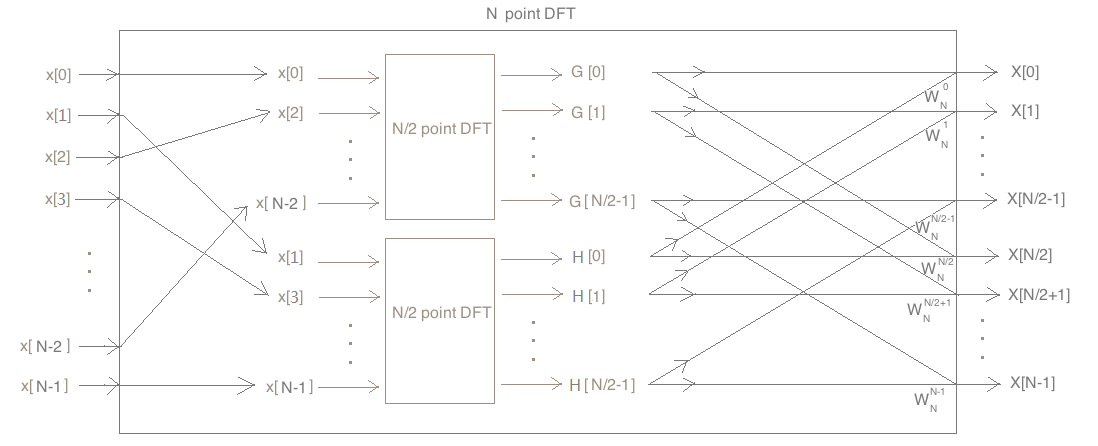
由此可见,可以用两个N/2个点的DFT处理器组装成N个点的DFT处理器。重复这一思想,那两个N/2个点的DFT处理器每个都可以由两个N/4个点的DFT处理器组成,由于N为2的幂,所以此过程可反复进行,直到分解为1个点的DFT处理器为止。
此即基于奇偶分治的FFT算法。
算法复杂度分析:
设使用上述FFT算法的情况下N point DFT所需乘法次数为C(N),则根据上面电路图显然有:
C(N)=2C(N/2)+N
又由于1个点的FFT所需乘法次数为1(即输入值x乘以 ),即
),即
C(1)=1
求解此递推公式,得
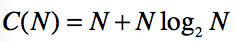
所以算法复杂度为O(N*logN)
参考:
https://www.youtube.com/watch?v=EsJGuI7e_ZQ
https://www.youtube.com/watch?v=1mVbZLHLaf0
----补充
一,
因为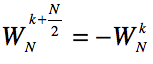 ,所以前面电路图可等价地优化为:
,所以前面电路图可等价地优化为:
参考:https://cnx.org/contents/zmcmahhR@7/Decimation-in-time-DIT-Radix-2 (其中Additional Simplification一节)。
二,
递推公式
C(N)=2C(N/2)+N
C(1)=1
求解过程如下:
令
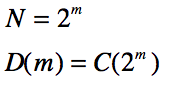
则
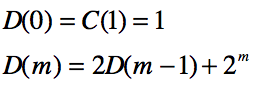
用累加法求解D(m),写:
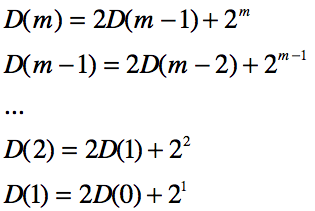
将第二式乘以2,将第三式乘以4,将第四式乘以8...然后累加,得:
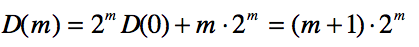
所以
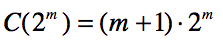
即
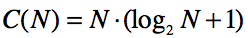
理顺FFT的更多相关文章
- 并行计算提升32K*32K点(32位浮点数) FFT计算速度(4核八线程E3处理器)
对32K*32K的随机数矩阵进行FFT变换,数的格式是32位浮点数.将产生的数据存放在堆上,对每一行数据进行N=32K的FFT,记录32K次fft的时间. 比较串行for循环和并行for循环的运行时间 ...
- 【BZOJ-2179&2194】FFT快速傅里叶&快速傅里叶之二 FFT
2179: FFT快速傅立叶 Time Limit: 10 Sec Memory Limit: 259 MBSubmit: 2978 Solved: 1523[Submit][Status][Di ...
- 为什么FFT时域补0后,经FFT变换就是频域进行内插?
应该这样来理解这个问题: 补0后的DFT(FFT是DFT的快速算法),实际上公式并没变,变化的只是频域项(如:补0前FFT计算得到的是m*2*pi/M处的频域值, 而补0后得到的是n*2*pi/N处的 ...
- FFT NNT
算算劳资已经多久没学新算法了,又要重新开始学辣.直接扔板子,跑...话说FFT算法导论里讲的真不错,去看下就懂了. //FFT#include <cstdio> #include < ...
- CC countari & 分块+FFT
题意: 求一个序列中顺序的长度为3的等差数列. SOL: 对于这种计数问题都是用个数的卷积来进行统计.然而对于这个题有顺序的限制,不好直接统计,于是竟然可以分块?惊为天人... 考虑分块以后的序列: ...
- ECF R9(632E) & FFT
Description: 上一篇blog. Solution: 同样我们可以用fft来做...就像上次写的那道3-idoit一样,对a做k次卷积就好了. 同样有许多需要注意的地方:我们只是判断可行性, ...
- fft练习
数学相关一直都好弱啊>_< 窝这个月要补一补数学啦, 先从基础的fft补起吧! 现在做了 道. 窝的fft 模板 (bzoj 2179) #include <iostream> ...
- FFT时域与频域的关系,以及采样速率与采样点的影响
首先对于FFT来说,输入的信号是一个按一定采样频率获得的信号序列,而输出是每个采样点对应的频率的幅度(能量). 下面详细分析: 在FFT的输出数据中,第一个值是直流分量的振幅(这样对应周期有无穷的可能 ...
- 【玩转单片机系列002】 如何使用STM32提供的DSP库进行FFT
前些日子,因为需要在STM32F103系列处理器上,对采集的音频信号进行FFT,所以花了一些时间来研究如何高效并精确的在STM32F103系列处理器上实现FFT.在网上找了很多这方面的资料做实验并进行 ...
随机推荐
- Codeforces 915F Imbalance Value of a Tree
Imbalance Value of a Tree 感觉这种题没啥营养, 排个序算算贡献就好啦. #include<bits/stdc++.h> #define LL long long ...
- js后退
history.back(-1):直接返回当前页的上一页,数据全部消息,是个新页面 history.go(-1):也是返回当前页的上一页,不过表单里的数据全部还在 history.back(0) 刷新 ...
- 089实战 Nginx的安装
1.上传 使用淘宝改进过的nginx 2.解压 tar -zxvf tengine-2.0.2.tar.gz -C ../modules/ 3.进入tegine主目录 4.安装依赖 sudo yu ...
- 038 关于HIVE的配置
一:常用版本 1.版本 0.13.1 2014年 1.2.1 2015年 版本之间的区别:支持SQL不同,向关系型数据库靠拢. 目前看到的版本是2.3.2了. 2.官网 二:安装配置hive 1. ...
- 如何查看Ubuntu版本,以及Linux内核版本??
查看Ubuntu版本: 方法一: cat /etc/issue 方法二: sudo lsb_release -a 查看内核版本: uname -r
- laravel 控制器使用MODEL
第一步:引入MODEL类 use App\Http\Models\Sysdba; 第二步:使用 $uid = $request->input('uid'); 方法1. $model = new ...
- Codeforces-542div2
https://www.cnblogs.com/31415926535x/p/10468017.html codeforces-1130A~G 和队友做了一套题,, A. Be Positive 题意 ...
- 打开Word时出现“The setup controller has encountered a problem during install. Please ...”
找到C:\Program Files\Common Files\Microsoft Shared\OFFICE12\Office Setup Controller,将这个文件夹删除或改名,就不再出现提 ...
- XHR对象
一.XMLHttpRequest对象 var xhr = new XMLHttpRequest(), i = 0; for(var key in xhr){ if(xhr.hasOwnProperty ...
- [BalticOI2014]Friends/[BZOJ4287]新三个和尚
[BalticOI2014]Friends/[BZOJ4287]新三个和尚 题目大意: 一个字符串\(A\),将\(A\)复制一遍并在任意位置插入一个新字符得到\(B\).给出\(B(|B|\le2\ ...
