树和二叉树->线索二叉树

文字描述

　　从二叉树的遍历可知，遍历二叉树的输出结果可看成一个线性队列，使得每个结点(除第一个和最后一个外)在这个线形队列中有且仅有一个前驱和一个后继。但是当采用二叉链表作为二叉树的存储结构时，只能得到结点的左孩子结点和右孩子结点，要想知道结点的前驱或后继，需要再遍历一次才知道。另外，叶子结点的左右孩子结点是空链域，在有n个结点的二叉链表中必定存在n+1个空链域，原因见[附录1证明]。由此，便可以考虑利用这些叶子结点的空链域来存放结点的前驱和后继结点。

　　线索二叉树的存储结构中增加两个标志域LTag和RTag，标志左/右链域是孩子结点还是前驱或后继。这种存储结构叫做线索存储，之前前驱和后继的结点指针叫线索，加上线索的二叉树叫线索二叉树。关于线索二叉树主要有两个问题需要解决：

　　第一个问题 如何建立线索二叉树？

　　第二个问题 如何遍历线索二叉树？

　　第一个问题：如何建立线索二叉树？

　　线索化的实质就是将二叉链表的空指针改为前驱或后继的线索。而前驱或后继的信息只有在遍历时才能得到，因此线索化的过程即为在遍历过程中修改空指针的过程。为了记下遍历过程中访问结点的先后关系，附设一个pre始终指向刚刚访问过的结点，若指针p指向当前访问的结点，则pre就是p的前去，p就是pre的后继。

　　第二个问题：如何遍历线索二叉树？

　　在线索树上遍历，只要先找到序列中的第一个结点，然后依次找结点后继直至后继为空时为止。树中所有叶子结点的链域就是线索，左链指示了该结点的前驱，右链域指示了该结点的后继，而如何在线索树中找非叶子结点的前驱或后继呢？

　　对于先序线索树 根据先序遍历的规律知，非终端结点的后继：如果其左孩子存在,则后继就是其左孩子结点. 否则后继就是其右孩子结点.

　　对于中序线索树 根据中序遍历的规律知，。非终端结点的后继应该是遍历其右子树时访问的第一个结点，即右子树中最左下的结点；

　　对于后序线索树 在后序线索树中找结点后继复杂些，分3种情况: (1)若结点x是二叉树的根，其后继就是为空；(2)若结点x是其双亲结点的右孩子或者 是其双亲的左孩子且其双亲没有右子树， 则其后继即为双亲结点 (3)若结点x是其双亲的左孩子，且双亲有右子树，则其后继为双亲的右子树上按后序遍历列出的第一个结点。可见，在后序线索树上找后继时需知道结点双亲，即需带标志域的三叉链表作存储结构。

示意图

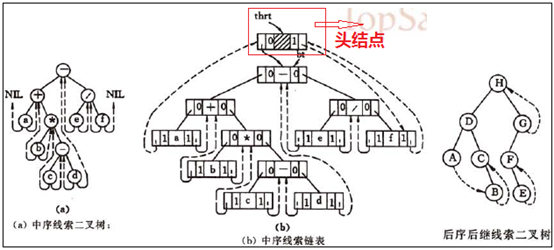
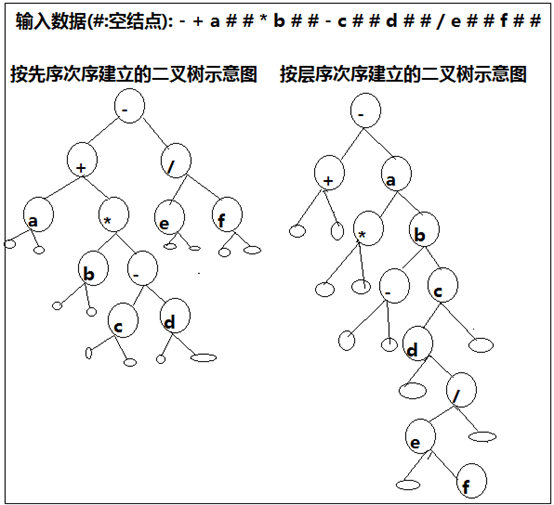
算法分析

　　线索二叉树上遍历二叉树，时间复杂度仍然为n， 但是常数因子要比非线索二叉树的遍历算法小，且不需要另外设栈或队列。 因此，若二叉树需要经常遍历或查找结点在遍历所得线性序列中的前驱和后继，则应采用线索链表做存储结构。

代码实现

 /*
  *
  * 编译本文件后，可输入如下参数:
  *
  * ./a.out - + a \# \# \* b \# \# - c \# \# d \# \# / e \# \# f \# \#
  *
  */

 #include <stdio.h>
 #include <stdlib.h>

 #define DEBUG
 #define EQ(a, b) ((a)==(b))
 /*树中结点的最大个数*/
 #define MAX_TREE_SIZE 100

 typedef char KeyType;
 typedef int InfoType;

 /*树中的结点类型*/
 typedef struct{
     KeyType key;
     InfoType otherinfo;
 }TElemType;

 /*Link==0指针，Thread==1线索*/
 typedef enum PointerTag{Link=, Thread}PointerTag; 

 /*
  * 二叉树的二叉线索存储表示
  *
  * 链表中的结点包含五个数据：数据域data，左指针域lchild，右指针域rchild, 左标志, 右标志
  */
 typedef struct BiTNode{
     TElemType data;
     struct BiTNode *lchild, *rchild;
     PointerTag LTag, RTag;
 }BiThrNode, *BiThrTree;

 /*
  * 创建二叉链表
  *
  * 按先根次序输入二叉树中结点的值，'#'表示空结点
  * 构造二叉链表表示的二叉树T
  */
 int I = ;
 BiThrTree CreateBiTree(TElemType input[]){
     TElemType data = input[I++];
     BiThrTree T = NULL;
     if(data.key == '#'){
         T = NULL;
         return T;
     }else{
         if(!(T=(BiThrNode *)malloc(sizeof(BiThrNode)))){
             printf("Error: overflow!\n");
             exit();
         }
         T->data = data;
         T->lchild = CreateBiTree(input);
         T->rchild = CreateBiTree(input);
         return T;
     }
 }

 /*遍历二叉树时用到的函数指针参数*/
 int vist(TElemType e){
     printf("%c ", e.key);
     return ;
 }

 /*
  * pre总指向刚刚访问过的结点，
  * 若p指向刚刚访问过的结点，则pre指向它的前驱；p指向pre的后继。
  */
 BiThrTree pre;

 //////////////////////////////////////////////////////////////////////////////////
 //先序线索二叉树的遍历与建立-start////////////////////////////////////////////////

 int PreOrderTraverse_Thr(BiThrTree Thrt, int (*fun)(TElemType e)){
     BiThrTree p = Thrt->lchild;
     while(p!=Thrt){
         fun(p->data);
         while(p->LTag == Link){
             p = p->lchild;
             fun(p->data);
         }
         p = p->rchild;
     }
     return ;
 }

 /*先序线索二叉树的建立*/
 void PreThreading(BiThrTree p){
     if(p){
         if(!p->lchild){
             p->LTag = Thread;
             p->lchild = pre;
         }
         if(!pre->rchild){
             pre->RTag = Thread;
             pre->rchild = p;
         }
         pre = p;
         if(p->LTag == Link)
             PreThreading(p->lchild);
         if(p->RTag == Link)
             PreThreading(p->rchild);
     }
     return ;
 }

 /*先序线索二叉树的建立*/
 BiThrTree PreOrderThreading(BiThrTree T){
     //建立头指针
     BiThrTree Thrt = NULL;
     if(!(Thrt=(BiThrTree)malloc(sizeof(BiThrNode)))){
         printf("malloc fail!\n");
         return NULL;
     }
     Thrt->LTag = Link;
     //右指针回值
     Thrt->RTag = Thread;
     Thrt->rchild = Thrt;
     if(!T){
         //若二叉树空，则右指针回指
         Thrt->lchild = Thrt;
     }else{
         Thrt->lchild = T;
         pre = Thrt;
         //中序线索化
         PreThreading(T);
         //最后一个结点线索化
         pre->RTag = Thread;
         pre->rchild = Thrt;
         Thrt->rchild = pre;
     }
     return Thrt;
 }

 //先序线索二叉树的遍历与建立-end///////////////////////////////////////////////
 ///////////////////////////////////////////////////////////////////////////////

 //////////////////////////////////////////////////////////////////////////////////
 //中序线索二叉树的遍历与建立-start////////////////////////////////////////////////
  void InThreading(BiThrTree p){
     if(p){
         //左子树线索化
         InThreading(p->lchild);
         //pre指向p的前驱
         if(!p->lchild){
             p->LTag = Thread;
             p->lchild = pre;
         }
         //p指向pre的后继
         if(!pre->rchild){
             pre->RTag = Thread;
             pre->rchild = p;
         }
         //保持pre指向p的前驱
         pre = p;
         //右子树线索化
         InThreading(p->rchild);
     }
     return ;
 }

 /*
  * 中序线索二叉树的建立
  *
  * 中序遍历二叉树T,并将其中序线索化，返回值指向线索化的头结点
  * 头结点的lchild域的指针指向二叉树的根结点，其rchild域的指针指向中序遍历时访问的最后一个结点；
  * 另外，令二叉树中序序列中的第一个结点的lchild域指针和最后一个结点rchild域的指针均指向头结点。
  */
 BiThrTree InOrderThreading(BiThrTree T){
     //建立头指针
     BiThrTree Thrt = NULL;
     if(!(Thrt=(BiThrTree)malloc(sizeof(BiThrNode)))){
         printf("malloc fail!\n");
         return NULL;
     }
     Thrt->LTag = Link;
     //右指针回值
     Thrt->RTag = Thread;
     Thrt->rchild = Thrt;
     if(!T){
         //若二叉树空，则右指针回指
         Thrt->lchild = Thrt;
     }else{
         Thrt->lchild = T;
         //pre总指向刚刚访问过的结点，若p指向刚刚访问过的结点，则pre指向它的前驱；p指向pre的后继。
         pre = Thrt;
         //中序遍历进行中序线索化
         InThreading(T);
         //最后一个结点线索化
         pre->RTag = Thread;
         pre->rchild = Thrt;
         Thrt->rchild = pre;
     }
     return Thrt;
 }

 /*
  * 中序线索二叉树的遍历
  */
 int InOrderTraverse_Thr(BiThrTree Thrt, int (*fun)(TElemType e)){
     BiThrTree p = Thrt->lchild;
     while(p!=Thrt){
         while(p->LTag==Link) p = p->lchild;
         fun(p->data);
         while(p->RTag==Thread && p->rchild != Thrt){
             p = p->rchild;
             fun(p->data);
         }
         p = p->rchild;
     }
     return ;
 }
 //中序线索二叉树的遍历与建立-end//////////////////////////////////////////////////
 //////////////////////////////////////////////////////////////////////////////////

 //////////////////////////////////////////////////////////////////////////////////
 //后序线索二叉树的遍历与建立-start///////////////////////////////////////////////
 /*三叉链表结构*/
 typedef struct BiPTNode{
     TElemType data;
     struct BiPTNode *lchild, *rchild, *parent;
     PointerTag LTag, RTag;
 }BiPThrNode, *BiPThrTree;

 ////////////////////////////////////////
 //与队列相关的结构体和函数声明-start////
 typedef struct QNode{
     BiPThrTree data;
     struct QNode *next;
 }QNode, *QuenePtr;

 typedef struct{
     QuenePtr front;
     QuenePtr rear;
 }LinkQueue;

 LinkQueue* InitQueue(void);
 int QueueEmpty(LinkQueue *Q);
 int GetHead(LinkQueue *Q, BiPThrTree *e);
 int EnQueue(LinkQueue *Q, BiPThrTree *e);
 int DeQueue(LinkQueue *Q, BiPThrTree *e);
 //与队列相关的结构体和函数声明-end////////
 //////////////////////////////////////////

 /*
  * 三叉链表的建立
  *
  * 按照层序遍历的顺序依次输入结点input， 然后建立带双亲结点的三叉链表。
  *
  */
 BiPThrTree CreatePBiTree(TElemType input[]){
     I = ;
     TElemType data;
     BiPThrTree PT = NULL, parent, lchild=NULL, rchild=NULL;
     if((data=input[I++]).key == '#'){
         return PT;
     }else{
         if(!(PT=(BiPThrNode *)malloc(sizeof(BiPThrNode)))){
             exit();
         }
         PT->data = data;
         PT->parent = NULL;
         LinkQueue *Q = InitQueue();
         EnQueue(Q, &PT);
         while(QueueEmpty(Q)){
             DeQueue(Q, &parent);
             if((data=input[I++]).key == '#'){
                 lchild = NULL;
             }else{
                 lchild = (BiPThrNode *)malloc(sizeof(BiPThrNode));
                 lchild->data = data;
                 lchild->parent = parent;
                 EnQueue(Q, &lchild);
             }
             (parent)->lchild = lchild;

             if((data=input[I++]).key == '#'){
                 rchild = NULL;
             }else{
                 rchild = (BiPThrNode *)malloc(sizeof(BiPThrNode));
                 rchild->data = data;
                 rchild->parent = parent;
                 EnQueue(Q, &rchild);
             }
             (parent)->rchild = rchild;
         }
     }
     return PT;
 }

 /*
  * pre_p总指向刚刚访问过的结点，
  * 若p指向刚刚访问过的结点，则pre_p指向它的前驱；p指向pre_p的后继。
  */
 BiPThrTree pre_p;

 void PostThreading(BiPThrTree p){
     if(p){
         PostThreading(p->lchild);
         PostThreading(p->rchild);
         if(!p->lchild){
             p->LTag = Thread;
             p->lchild = pre_p;
         }
         if(!pre_p->rchild){
             pre_p->RTag = Thread;
             pre_p->rchild = p;
         }
         pre_p = p;
     }
     return ;
 }

 /*后序线索二叉树的建立*/
 BiPThrTree PostOrderThreading(BiPThrTree T){
     BiPThrTree Thrt = NULL;
     if(!(Thrt=(BiPThrTree)malloc(sizeof(BiPThrNode)))){
         return NULL;
     }
     Thrt->LTag = Link;
     Thrt->RTag = Thread;
     Thrt->rchild = Thrt;
     if(!T){
         Thrt->lchild = Thrt;
     }else{
         Thrt->lchild = T;
         pre_p = Thrt;
         PostThreading(T);
         pre_p->RTag = Thread;
         pre_p->rchild = Thrt;
         Thrt->rchild = pre_p;
     }
 }

 /*后序线索二叉树的遍历*/
 void PostOrderTraverse_Thr(BiPThrTree Thrt, int (*fun)(TElemType e))
 {
     BiPThrTree p = Thrt->lchild;
     while(p->LTag == Link){
         p = p->lchild;
     }
     while(p!=Thrt){
         fun(p->data);
         while(p->RTag==Thread && p->rchild != Thrt){
             p = p->rchild;
             fun(p->data);
         }
         if(p->parent){
             p = p->parent;
         }else{
             break;

         }
     }
 }
 //后序线索二叉树的遍历与建立-end//////////////////////////////////////////////////
 //////////////////////////////////////////////////////////////////////////////////

 int main(int argc, char *argv[])
 {
     if(argc < )
         return -;

     TElemType input[MAX_TREE_SIZE];
     int i = , j = ;
     for(i=; i<MAX_TREE_SIZE; i++){
         input[i].key = '#';
     }

     //按先根次序输入二叉树中结点的值，'#'表示空树
     for(i=; i<argc; i++){
         if(i>MAX_TREE_SIZE)
             break;
         input[i-].key = argv[i][];
         input[i-].otherinfo = i-;
     }
 #ifdef DEBUG
     printf("输入数据以建立二叉树(#表示空空结点):\n");
     for(j=; j< i-; j++){
         printf("%c ", input[j].key);
     }
     printf("\n");
 #endif
     printf("先序线索二叉树的建立与遍历:(按照先序次序建立二叉树)\n");
     I=;
     BiThrTree PreT = CreateBiTree(input);
     BiThrTree PreThrt = PreOrderThreading(PreT);
     PreOrderTraverse_Thr(PreThrt, vist);

     printf("\n中序线索二叉树的建立与遍历:(按照先序次序建立二叉树)\n");
     I = ;
     BiThrTree InT = CreateBiTree(input);
     BiThrTree InThrt = InOrderThreading(InT);
     InOrderTraverse_Thr(InThrt, vist);

     printf("\n后序线索二叉树的建立与遍历:(按照层序次序建立二叉树)\n");
     I=;
     BiPThrTree PostT = CreatePBiTree(input);
     BiPThrTree PostThrt = PostOrderThreading(PostT);
     PostOrderTraverse_Thr(PostThrt, vist);
     printf("\n");
     return ;
 }

 //////////////////////////////////////////////////////////////////////////////////
 //与队列相关的函数的实现-start///////////////////////////////////////////////////
 LinkQueue* InitQueue(void)
 {
     LinkQueue *Q = (LinkQueue*)malloc(sizeof(LinkQueue));
     Q->front = Q->rear = (QuenePtr)malloc(sizeof(QNode));
     if(!Q->front){
         printf("malloc fail!\n");
         return NULL;
     }
     return Q;
 }

 int QueueEmpty(LinkQueue *Q)
 {
     if(Q->front == Q->rear){
         return ;
     }else{
         return -;
     }
 }

 int GetHead(LinkQueue *Q, BiPThrTree *e)
 {
     if(Q->front == Q->rear){
         return -;
     }
     *e = Q->front->next->data;
     return ;
 }

 int EnQueue(LinkQueue *Q, BiPThrTree *e)
 {
     QuenePtr p = (QuenePtr)malloc(sizeof(QNode));
     if(!p){
         printf("malloc fail!\n");
         return -;
     }
     p->data = *e;
     p->next = NULL;
     Q->rear->next = p;
     Q->rear = p;
     return ;
 }

 int DeQueue(LinkQueue *Q, BiPThrTree *e)
 {
     if(Q->front == Q->rear){
         return -;
     }
     QuenePtr p = Q->front->next;
     *e = p->data;
     Q->front->next = p->next;
     if(p == Q->rear){
         Q->rear = Q->front;
     }
     free(p);
     return ;
 }
 //与队列相关的函数的实现-end//////////////////////////////////////////////////////
 //////////////////////////////////////////////////////////////////////////////////

线索二叉树的建立与遍历

运行

附录1

　　证明n个结点的二叉链表中必有n+1个空链域：

　　n个结点的二叉链表中共有n*2个链域，除根结点外的每个结点都有一个父亲结点，所以2*n个链域中有n-1个有内容的链域。所以共有2*n-(n-1) = n+1个空链域 。