AcWing：131. 直方图中最大的矩形（贪心 + 单调栈）

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

例如，图例左侧显示了由高度为2,1,4,5,1,3,3的矩形组成的直方图，矩形的宽度都为1：

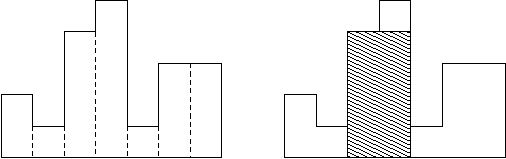
通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数n开始，表示组成直方图的矩形数目。

然后跟随n个整数h1，…，hnh1，…，hn。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为1。

同行数字用空格隔开。

当输入用例为n=0时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1≤n≤1000001≤n≤100000,
0≤hi≤10000000000≤hi≤1000000000

输入样例：

7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

8
4000

算法：贪心 + 单调栈

#include <iostream>
#include <cstdio>
#include <stack>

using namespace std;

typedef long long ll;

const int maxn = 1e5+;

int vis[maxn];

int main() {
    int n;
    while(scanf("%d", &n) && n) {
        ll ans = ;
        stack<ll> s;
        for(int i = ; i <= n; i++) {
            ll x;
            scanf("%lld", &x);
            if(s.empty() || x >= s.top()) {
                s.push(x), vis[s.size()] = ;
            } else {
                int cnt = ;
                while(!s.empty() && x < s.top()) {
                    cnt += vis[s.size()];
                    ans = max(ans, 1LL * cnt * s.top());
                    s.pop();
                }
                s.push(x);
                vis[s.size()] = cnt + ;    //记录在他之前经过了多少个比自身大的数(加一的意思事本身也要算上)
            }
        }
        int cnt = ;
        while(!s.empty()) {
            cnt += vis[s.size()];
            ans = max(ans, 1LL * cnt * s.top());
            s.pop();
        }
        cout << ans << endl;
    }
    return ;
}