2019.7.9 校内测试 T3 15数码问题

这一次是交流测试？边交流边测试（滑稽

15数码问题

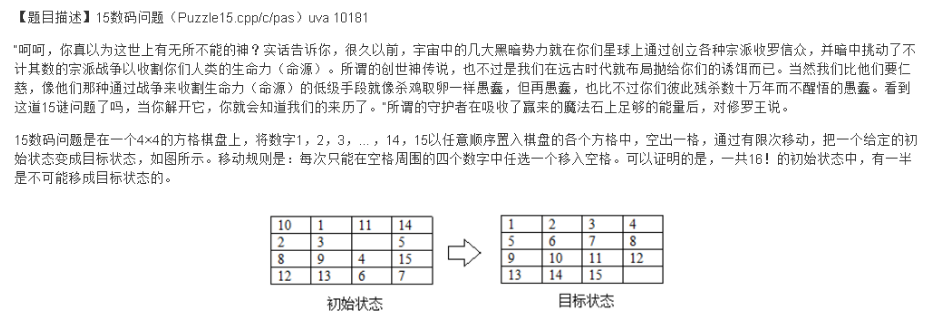
大家应该都玩过这个15数码的游戏吧，就在桌面小具库那里面哦。

一看到这个题就知道要GG，本着能骗点分的原则输出了 t 个无解，本来以为要爆零，没想到这个题数据是真的水，全输出无解能骗到40分，某些大佬输出样例了又骗到了20分 QwQ~；

本题对应着洛谷的UVA10181 15-Puzzle Problem ，省选难度，果然不简单QwQ~，_rqy 讲了一番，听得糊里糊涂。

这个题正解是搜索（貌似是废话，都给了15s的时间了），但是还是需要一些剪枝的。

剪枝一：未做此题先判其解

看着这四四方方的格子，不大好搞啊，所以我们可以抽象的把这些数字给整到一行去，比如我们把上面的情况给整成这样：

所以我们最后要搞成这样是吧：

所以我们可以换个角度来思考问题：

考虑到最终目标无逆序对，所以我们可以将问题转化为：求交换多少次能使原长串的逆序对给弄成0！

因为我们每交换一下相邻的两个数字，整个序列的逆序对的奇偶性就会改变。（逆序对数是偶数就显偶性，是奇数就显奇性）

所以如果原序列的逆序对是奇性的话，我们至少要进行奇数次操作；是偶性的话，我们至少要进行偶数次操作；

然后我们可以求出原序列的逆序对数，先判断答案的奇偶性；

于是这里用到一个定理：设初始状态0所在的行数为i,目标状态0所在的行数为j，两者之差的绝对值为k。若k为奇数，则两个矩阵相应的逆序数的奇偶性相异才有解。若k为偶数，则两个矩阵的逆序数必须相同才有解。不是上述两种情况即为无解。通过初始判定就可以不用搜索就能直接否定无解情况。

剪枝二：从最小步数开始搜

我们每进行一步操作，对应的数字会往目标值更近一步。

假如我们这个位置有个 12，我们一步一步得将它移到目标位置，那么我们最少步数就是 3 ：

怎么算呢？就是终点的横纵坐标再减去起点的横纵坐标的绝对值再相加便可以得到，这个距离叫曼哈顿距离。（大雾

标准定义（好像跟我口胡得差不多）：

曼哈顿距离：在标准坐标系中，两点的x坐标差的绝对值与y坐标差的绝对值之和为曼哈顿距离。

int manhattan(int a[][size])//计算曼哈顿距离，小等于实际总步数
{
  int i,j,cost=;
  for(i=;i<size;i++)
    for(j=;j<size;j++)
    {
      int w=map[i][j];
      cost+=abs(i-goal[w][])+abs(j-goal[w][]);
    }
  return cost;
}

作用：求出初始矩阵与目标矩阵对应值得曼哈顿距离并求和（除去0）得到的值为评估值，写成函数即为评估函数。该值为从初始状态到目标状态所要经过的最小步数，实际步数只会大于等于该值。

算法介绍：这次使用的算法是IDA*。我们首先是用逆序数进行判定是否有解，有解才进行搜索。有解的话，则先得到评估函数的初始值，该值为最小步数，递归深度（步数）必然大于等于这个初始值limit。我们先按深度搜索寻遍该深度的所有情况，看是否能找到解，有解则该解是最优解。若没解，则将深度的限制条件limit加1，再次递归下一层深度的所有情况，有解即为最优解，无解则继续将深度限制条件limit加1，这样不停循环直到某个深度maxLevel，则放弃寻找，因为在maxLevel步中没有找到，继续找下去时间花销太高，故放弃寻找。这就是IDA*中ID的意思，迭代加深。其中，算法在递归中使用了当前递归深度level,用level+评估函数(当前状态到目标状态至少需要的步数)<=limit作为剪枝条件，不满足该条件的在该分支上肯定无解。这样我们就可以找到在maxLevel步以内的最优解。

So，完整标程代码如下：（大雾

//１５数码问题
#include<iostream>
#include<cstdlib>
#include<cmath>
#define size 4
using namespace std;
 
int move[][]={{-,},{,-},{,},{,}};//上,左,右,下增量
char op[]={'U','L','R','D'};
int map[size][size],map2[size*size],limit,path[];
int flag,length;
//int goal_st[3][3]={{1,2,3},{4,5,6},{7,8,0}};//目标状态
//goal存储目标位置，即０存在（３,３）,1存在（0,0）...
int goal[][]= {{,},{,},{,}, {,},
                  {,},{,},{,}, {,},
                  {,},{,},{,}, {,},
                  {,},{,},{,}, {,}};
 
int h(int a[size*size])//求逆序数
{
  int i,j,num,w,x,y;
  num=;
  for(i=;i<size*size;i++)
  {
    if(a[i]==)
      w=i;
    for(j=i+;j<size*size;j++)
    {
      if(a[i]>a[j])
        num++;
    }
  }
  x=w/size;
  y=w%size;
  num+=abs(x-)+abs(y-);
  if(num%==)
    return ;
  else
    return ;
}
 
int manhattan(int a[][size])//计算曼哈顿距离，小等于实际总步数
{
  int i,j,cost=;
  for(i=;i<size;i++)
    for(j=;j<size;j++)
    {
      int w=map[i][j];
      cost+=abs(i-goal[w][])+abs(j-goal[w][]);
    }
  return cost;
}
 
void swap(int*a,int*b)
{
  int tmp;
  tmp=*a;
  *a=*b;
  *b=tmp;
}
 
void dfs(int sx,int sy,int dep,int pre_move)//sx,sy是空格的位置
{
  int i,j,nx,ny;
  if(flag)
    return;
  int dv=manhattan(map);
  if(dep==limit)
  {
    if(dv==)
    {
      flag=;
      length=dep;
      return;
    }
    else
      return;
  }
  else if(dep<limit)
  {
    if(dv==)
    {
      flag=;
      length=dep;
      return;
    }
  }
  for(i=;i<;i++)//４个方向尝试
  {
    if(i+pre_move==&&dep>)//不和上一次移动方向相反，对第二步以后而言
      continue;
    nx=sx+move[i][];
    ny=sy+move[i][];
    if(<=nx && nx<size && <=ny&&ny<size)//如果可以移动
    {
       swap(&map[sx][sy],&map[nx][ny]);//交换两位置
       int p=manhattan(map);
       if(p+dep<=limit&&!flag)
       {
          path[dep]=i;
         dfs(nx,ny,dep+,i);
         if(flag)
           return;
       }
       swap(&map[sx][sy],&map[nx][ny]);
    }
  }
}
 
int main()
{
  freopen("Puzzle15.in","r",stdin);
  freopen("Puzzle15.out","w",stdout);
  int i,j,k,l,m,n,sx,sy;
  char c,g;
  i=;
  scanf("%d",&n);
  while(n--)
  {
    flag=;length=;
    memset(path,-,sizeof(path));
    for(i=;i<;i++)
    {
      scanf("%d",&map2[i]);
      if(map2[i]==)
      {
        map[i/size][i%size]=;
        sx=i/size;sy=i%size;
      }
      else
      {
        map[i/size][i%size]=map2[i];
      }
    }
    if(h(map2)==)//该状态可达
    {
      limit=manhattan(map);
      while(!flag&&length<=)//题中要求50步之内到达
      {
        dfs(sx,sy,,);
        if(!flag)
          limit++; //得到的是最小步数
      }
      if(flag)
      {
        for(i=;i<length;i++)
          printf("%c",op[path[i]]);
        printf("\n");
      }
    }
    else if(!h(map2)||!flag)
      printf("This puzzle is not solvable.\n");
  }
  return ;
}

终于口胡完了QwQ~（话说我竟然除了代码其他好像都懂了）