DP&图论 DAY 6 上午

DP&图论  DAY 6  上午

双连通分量

从u-->v不存在必经边，点

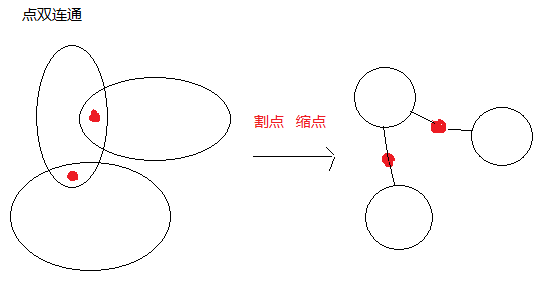
点双连通分量

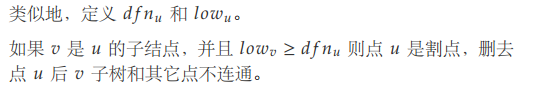
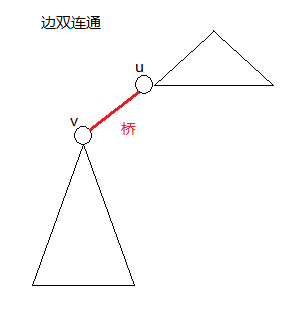
边双连通分量

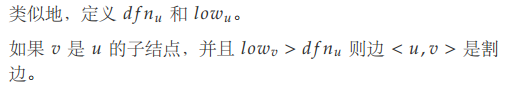
点/边双连通分量缩点之后变成一个树

找连通块的时候不越过割点或者桥

P3469 [POI2008]BLO-Blockade

1.不删割点，减少 2（n-1）

2.删割点，图分裂多个联通快，连通块大小*其他所有连通块大小

缩点之后得到一个树

P2860 [USACO06JAN]冗余路径Redundant Paths

缩点之后变成树，加多少边

二分图

无向图

二分图：点黑白染色，邻点不同色。

>

二分图的等价条件

二分图匹配

分成两列，左右相连

匈牙利算法

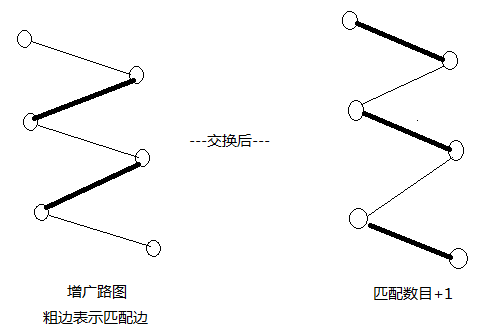
匹配边比非匹配边少1，然后交换，匹配边多1

dfs

一个点的匹配边只有一个

网络流

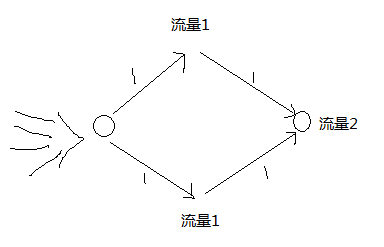
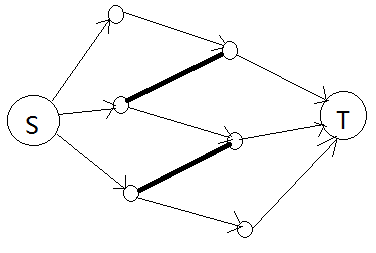
最小顶点覆盖 Knoig 定理

一个点，可以选中所有临边

国际棋盘是黑白染色的

POJ 3041 Asteroids

Solution

坐标图建图

x  坐标一列， y 坐标一列，然后对于一个坐标，x 坐标向 y 坐标连边

最小覆盖=最大匹配

最小路径覆盖

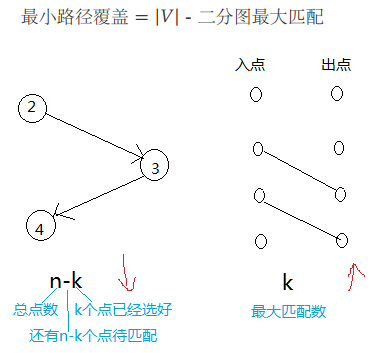
原图中的路径和二分图中的匹配数是一一对应的

要使得每个点唯一入度唯一出度，才能保证匹配

一个选中的边确定了一个出点得到匹配

没有入边的点只能放飞自我等待匹配

BZOJ 2150 部落战争

Solution

差分约束

BZOJ 2330糖果

 

Solution

1.建边

X=1    A >= B&&A <= B

X=2    A <= B-1

X=3    A >= B

X=4    A >= B+1

X=5    A <= B

因为在求最长路的时候，保证的是 if(dis[v]<dis[u]+w)  dis[v]=dis[u]+w ， 所以是改成 >=

( 其实最长路是最小的最长路

2.建超级远点，与每个点连边 1

从超级远点出发跑最长路，可能有负数，SPFA

BZOJ 1202狡猾的商人

Solution

这题都是等式

以 Si 表示 Ai 的前缀和，则每个限制形如 Su - Sv=k，将其拆
分为两个不等式
   # Su - Sv ≤ k
   # Su - Sv ≥ k 即 Sv - Su ≤ -k
差分约束后如果出现负环，则信息有假。
当然，对于这种全部为等式的差分约束问题，用 DFS 或 BFS 判
断即可，不需要应用最短路算法。

BZOJ 4500 矩阵

a.cpp

 Solution