2019 南昌ICPC网络赛H The Nth Item

The Nth Iteam

题意：F(0)=1,F(1)=1，F(n)=3*F(n-1)+2*F(n-2) (n>=2) ,F(n) mod 998244353。给出Q跟N₁,N_i=N_i-1^(F(N_i-1)*F(N_i-1)),求F(N₁)^F(N₂)^...^F(N_Q）

这个比赛的E跟H数据都水得很，但题还是不错的。

比赛时是求了个循环节，又进行了矩阵的降幂，然后本地+测试在时限内跑出了几组1e7的数据，才敢交的，但没想到数据那么水，矩阵快速幂+map记忆化一下就能过。

 #include<cstdio>
 #include<tr1/unordered_map>
 using namespace std;
 typedef long long ll;
 const int N=1e7+,md=;
 tr1::unordered_map<ll,int> mmp;
 ll aa[N],f[N];
 struct Matrix{
     int r,c;
     ll a[][];
     Matrix(){}
     Matrix(int r,int c):r(r),c(c){
         for(int i=;i<r;i++)
             for(int j=;j<c;j++) a[i][j]=;
     }
 };
 Matrix mmul(Matrix m1,Matrix m2,ll z){
     Matrix ans(m1.r,m2.c);
     for(int i=;i<m1.r;i++)
         for(int j=;j<m2.c;j++)
             for(int k=;k<m1.c;k++){
                 ans.a[i][j]+=m1.a[i][k]*m2.a[k][j]%z;
                 if(ans.a[i][j]>=z) ans.a[i][j]-=z;
             }
     return ans;
 }
 Matrix mpow(Matrix m1,ll y,ll z){
     Matrix ans(m1.r,m1.c);
     for(int i=;i<ans.r;i++) ans.a[i][i]=;
     while(y){
         if(y&) ans=mmul(ans,m1,z);
         m1=mmul(m1,m1,z);
         y>>=;
     }
     return ans;
 }
 
 int main(){
     f[]=;f[]=;
     for(int i=;i<N;i++) f[i]=(f[i-]*3ll%md+f[i-]*2ll%md)%md;
     int q,pos1,pos2,len,num,yu;
     ll n,m,ans;
     while(~scanf("%d%lld",&q,&n)){
         ans=aa[]=;
         mmp.clear();
         pos1=pos2=-;
         for(int i=;i<=q;i++){
             if(n<N) aa[i]=f[n];
             else{
                 m=n-;
                 if(m>=md-) m%=md-;
                 Matrix A(,),T(,);
                    A.a[][]=;
                    T.a[][]=;T.a[][]=;T.a[][]=;
                 T=mpow(T,m,md);
                 A=mmul(T,A,md);
                 aa[i]=A.a[][];
             }
             if(n==) break;
             if(mmp[n]){
                 pos1=mmp[n];
                 pos2=i;
                 break;
             }
             else mmp[n]=i;
             ans^=aa[i];
             n=n^(aa[i]*aa[i]);
             aa[i]^=aa[i-];
         }
         if(pos1!=-){
             len=pos2-pos1;
             num=(q-pos2+)/len;
             yu=(q-pos2+)%len;
             if(num&) ans^=aa[pos2-]^aa[pos1-];
             if(yu) ans^=aa[pos1+yu-]^aa[pos1-];
         }
         printf("%lld\n",ans);
     }
     return ;
 }

不应该过呀

但其实自己想一下，Q等于1e7，中间再套log的话，还有算矩阵快速幂时的一些常数，很明显就会T掉，水过去之余还是来学一些O(1)的处理方法。

首先这个数列显然是个线性递推数列，那么我们就可以求它的一个通项公式，具体求法360百科有好几个，我直接学习了第一个,方法：利用特征方程（线性代数解法）的解法。

下面是斐波那契数列通项公式的求解过程，我们依照此来求：

特征方程的概述

一个数列:X(n+2)=C1X(n+1)+C2Xn

设r，s使X(n+2)-rX(n+1)=s［X(n+1)-rXn］

所以X(n+2)=(s+r)X(n+1)-srXn

C1=s+r

C2=-sr

消去s就导出特征方程式 r*r-C1*r-C2=0

我们把C1=3,C2=2代入就有可以解除r=(3+√17)/2,s=(3-√17)/2

然后F(n)=x₁*rⁿ+x₂*sⁿ,我们把F(0)=0,F(1)=1,代入就能解得x₁=1/√17,x₂=-1/√17

那么上诉数列的通项公式就是F(n)=1/√17*(((3+√17)/2)ⁿ-((3-√17)/2)ⁿ)

这个解法包含不少线性代数的知识，不明白的可以去学一下那个待定系数等比数列求法，或者看一下这个斐波那契数列通项公式是怎样推导出来的？，里面有矩阵的推导过程。

回到这题，我们有了通项公式，√17的话，前面的博客就有讲到二次剩余，那么通过x²≡17（mod 998244353）可以求出x来代替√17,然后里面的除法我们可以求逆元，这些都可以先求出了。

相关代码如下：

 #include<cstdio>
 #include<ctime>
 #include<cstdlib>
 #include<algorithm>
 using namespace std;
 const int md=;
 typedef long long ll;
 struct Fp2{
     ll x,y;
 };
 ll w;
 Fp2 fmul(const Fp2 &f1,const Fp2 &f2){
     Fp2 ans;
     ans.x=(f1.x*f2.x%md+f1.y*f2.y%md*w%md)%md;
     ans.y=(f1.x*f2.y%md+f1.y*f2.x%md)%md;
     return ans;
 }
 Fp2 fpow(Fp2 x,ll y){
     Fp2 ans;
     ans.x=;ans.y=;
     while(y){
         if(y&) ans=fmul(ans,x);
         x=fmul(x,x);
         y>>=;
     }
     return ans;
 }
 ll poww(ll x,ll y){
     ll ans=;
     while(y){
         if(y&){
             ans*=x;
             if(ans>=md) ans%=md;
         }
         x*=x;
         if(x>=md) x%=md;
         y>>=;
     }
     return ans;
 }
 ll cipolla(ll x){
     if(x==) return ;
     if(x==) return ;
     if(poww(x,(md-)>>)+==md) return -;
     ll a;
     while(true){
         a=rand()%md;
         w=((a*a%md-x)%md+md)%md;
         if(poww(w,(md-)>>)+==md) break;
     }
     Fp2 ans;
     ans.x=a;ans.y=;
     ans=fpow(ans,(md+)>>);
     return ans.x;
 }
 int main(){
     srand(time(NULL));
     ll py17=cipolla(),nv2=poww(,md-);
     printf("根号17的二次剩余：%lld\n",py17);
     printf("2的逆元：%lld\n",nv2);
     printf("根号17的二次剩余的逆元：%lld\n",poww(py17,md-));
     printf("3+根号7除2：%lld\n",((+py17)%md*nv2%md)%md);
     printf("3-根号7除2：%lld\n",(((-py17)%md+md)%md*nv2%md)%md);
     return ;
 }

打表鸭

其中一组结果：

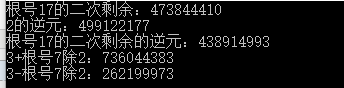
那么这时，我们设aa=736044383,bb=262199973,我们快速幂就可以log求出F(n)

但这还不够，我们需要的是O(1),所以我们可以先分块预处理。

怎么做呢，这时的aa,bb在 mod 998244353的意义下，已经是整数了，所以求aaⁿ或者bbⁿ在n很大时，就可以进行我们前面指数循环节里的欧拉降幂了，也就是n=n%998244352+998244352（998244352是998244353是欧拉函数）

这时n最大是1996488703，√1996488703=44682.084810357719028060186400879，那么我们可以把5e4（大于等于44683都可以）为一组分块，这样我们先预处理出aa跟bb的0次幂，1次幂，到5e4次幂，然后再预处理0*5e4次幂，1*5e4次幂到5e4*5e4次幂

那么当我们要求aa或者bb的n次幂时其实就是求（n/5e4)（整除）*5e4次幂 * n%5e4次幂，也就是设N=5e4，那么 n=q*N+r，q=n/N,r=n%N

这样我们就可以在O(1)求出相应的F(n)，

 #include<cstdio>
 typedef long long ll;
 const int N=5e4,md=;
 const ll nv17=,aa=,bb=;
 typedef long long ll;
 ll a[N+],af[N+],b[N+],bf[N+];
 void init(){
     a[]=b[]=;
     for(int i=;i<=N;i++){
         a[i]=a[i-]*aa;
         if(a[i]>=md) a[i]%=md;
         b[i]=b[i-]*bb;
         if(b[i]>=md) b[i]%=md;
     }
     af[]=bf[]=;
     for(int i=;i<=N;i++){
         af[i]=af[i-]*a[N];
         if(af[i]>=md) af[i]%=md;
         bf[i]=bf[i-]*b[N];
         if(bf[i]>=md) bf[i]%=md;
     }
 }
 int main(){
     init();
     int q;
     ll n;
     while(~scanf("%d%lld",&q,&n)){
         ll ans=,fn,m;
         while(q--){
             if(n==) break;
             m=n;
             if(m>=md-) m=m%(md-)+(md-);
             fn=((af[m/N]*a[m%N])%md)-((bf[m/N]*b[m%N])%md);
             fn=(fn%md+md)%md;
             fn*=nv17;
             if(fn>=md) fn%=md;
             ans^=fn;
             n=n^(fn*fn);
         }
         printf("%lld\n",ans);
     }
     return ;
 }

嘤嘤嘤

但由于数据的问题，预处理在计蒜客上实际运行时间还没直接套矩阵快速幂的快，自己出几个大数据就可看出哪个更快了，但我们不要被数据影响了，学到东西才是关键了。

总的来说，这题涉及到了线性递推数列的通项公式，二次剩余，逆元，还有分块思想，是个很不错的题。