【BZOJ2395】[Balkan 2011]Timeismoney

【BZOJ2395】[Balkan 2011]Timeismoney

题面

\(darkbzoj\)

题解

如果我们只有一个条件要满足的话直接最小生成树就可以了，但是现在我们有两维啊。。。

我们将每个方法的费用和时间看作一个二维坐标\((x,y)\)

则我们要求\(x\centerdot y=k\)最小即要求反比例函数\(y=\frac kx\)的图像离坐标轴最近。

那么我们怎么求呢？分下面三步：

• \(Step1\)

分别求出离\(y,x\)轴最近的点，这个通过直接最小生成树一维排序可以求出。

• \(Step2\)

现在我们的情况是这样的：

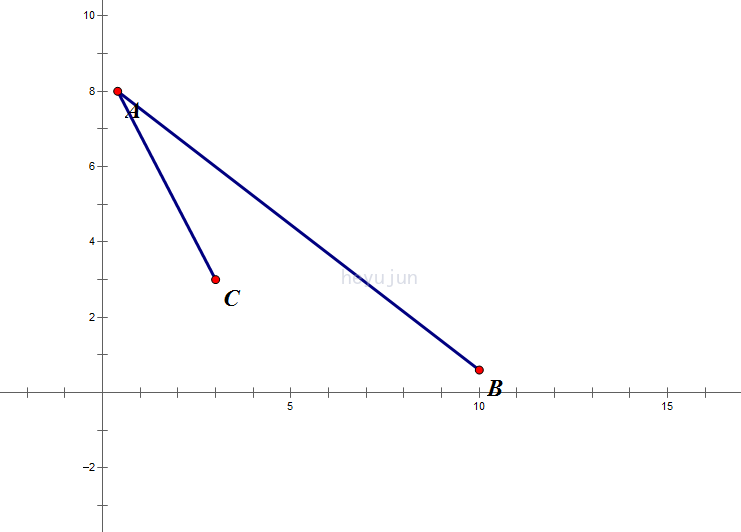
\(A\),\(B\)是我们刚才固定的，现在我们需要找到一个点\(C\)，使\(C\)在\(AB\)左侧且离\(AB\)最远。

这个怎么办呢？

其实就是让\(S_{\triangle ABC}\)的面积最大。

因为有

\[\vec {AB}=(B.x-A.x,B.y-A.y)\\
\vec {AC}=(C.x-A.x,C.y-A.y)
\]

且有\(S_{\triangle ABC}=\frac {\vec{AB}*\vec{AC}}2\)(但是这个面积是有向的且为负，所以要使这两个向量乘起来最小)

所以我们要最小化：

\[\vec{AB}*\vec{AC}\\
=(B.x-A.x)*(C.y-A.y)-(B.y-A.y)*(C.x-A.x)\\
=(B.x-A.x)*C.y+(A.y-B.y)*C.x+...
\]

因为我懒后面部分是常数，所以省略了。

那么我直接将改边权为\((B.x-A.x)y[i]+(A.y-B.y)x[i]\)，做最小生成树即可。

• \(Step3\)

现在找到了\(C\)，递归处理\((A,C)\)、\((C,B)\)即可。

终止条件\(\vec {BA} * \vec{CA}\geq0\)，说明此时\(C\)已经跑到\(AB\)右侧去了。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
const int MAX_N = 205;
const int MAX_M = 1e4 + 5;
struct Point { int x, y; } ;
Point ans = {(int)1e9, (int)1e9};
Point operator - (const Point &l, const Point &r) { return (Point){l.x - r.x, l.y - r.y}; }
int cross(const Point &l, const Point &r) { return l.x * r.y - l.y * r.x; }
int N, M, pa[MAX_N], rnk[MAX_N];
int getf(int x) { return pa[x] == x ? x : pa[x] = getf(pa[x]); }
inline void unite(int x, int y) {
    x = getf(x), y = getf(y);
    if (rnk[x] == rnk[y]) pa[x] = y, ++rnk[y];
    else (rnk[x] < rnk[y]) ? (pa[x] = y) : (pa[y] = x);
}
struct Edge { int u, v, c, t, w; } e[MAX_M];
inline bool operator < (const Edge &l, const Edge &r) { return l.w < r.w; }
#define RG register
inline Point kruskal() {
    Point res = (Point){0, 0};
    int tot = 0;
    for (RG int i = 1; i <= N; ++i) pa[i] = i, rnk[i] = 1;
    sort(&e[1], &e[M + 1]);
    for (RG int i = 1; i <= M; ++i) {
        int u = getf(e[i].u), v = getf(e[i].v);
        if (u != v) unite(u, v), res.x += e[i].c, res.y += e[i].t, ++tot;
        if (tot == N - 1) break;
    }
    long long Ans = 1ll * ans.x * ans.y, now = 1ll * res.x * res.y;
    if (Ans > now || (Ans == now && res.x < ans.x)) ans = res;
    return res;
}
void Div(const Point &A, const Point &B) {
    for (RG int i = 1; i <= M; ++i) e[i].w = e[i].t * (B.x - A.x) + e[i].c * (A.y - B.y);
    Point C = kruskal();
    if (cross(B - A, C - A) >= 0) return ;
    Div(A, C); Div(C, B);
}
int main() {
#ifndef ONLINE_JUDGE
    freopen("cpp.in", "r", stdin);
#endif
    scanf("%d%d", &N, &M);
    for (RG int i = 1; i <= M; i++) scanf("%d%d%d%d", &e[i].u, &e[i].v, &e[i].c, &e[i].t);
    for (RG int i = 1; i <= M; i++) ++e[i].u, ++e[i].v, e[i].w = e[i].c;
    Point A = kruskal();
    for (RG int i = 1; i <= M; i++) e[i].w = e[i].t;
    Point B = kruskal();
    Div(A, B);
    printf("%d %d\n", ans.x, ans.y);
    return 0;
}

为什么标签有个凸包呢？因为你满足要求的决策点肯定在凸包上啊