ZOJ 2587 Unique Attack（最小割唯一性判断）

http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=2587

题意：
判断最小割是否唯一。

思路：

最小割唯一性的判断是先跑一遍最大流，然后在残留网络中分别从源点和汇点出发dfs，只有当该边还有流量可用时可以访问下一个顶点，最后如果所有顶点都访问了，那么就是唯一的，否则不唯一。

接下来图解一下：

先看下面这个容量均为1的图：

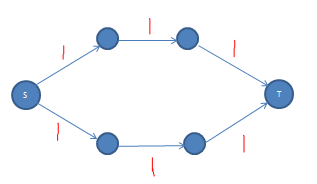
跑一遍最大流后的残留网络如下（只画正向弧）：

接下来从源点和汇点出发都无法访问任何顶点，因为剩余流量皆为0了。这种情况下最小割是不唯一的，很明显，这图我们可以找到很多最小割。

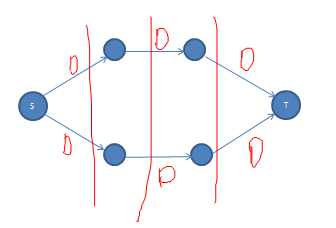
接下来看另外一个残留网络（只画正向弧）：

在这个网络中我们就可以遍历所有点，所以它的最小割是唯一的，也就是：

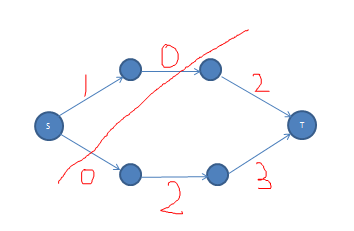
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,int> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn =  + ;

 int n, m, a, b;
 int vis[maxn];

 struct Edge
 {
     int from,to,cap,flow;
     Edge(int u,int v,int w,int f):from(u),to(v),cap(w),flow(f){}
 };

 struct Dinic
 {
     int n,m,s,t;
     vector<Edge> edges;
     vector<int> G[maxn];
     bool vis[maxn];
     int cur[maxn];
     int d[maxn];

     void init(int n)
     {
         this->n=n;
         for(int i=;i<n;++i) G[i].clear();
         edges.clear();
     }

     void AddEdge(int from,int to,int cap)
     {
         edges.push_back( Edge(from,to,cap,) );
         edges.push_back( Edge(to,from,,) );
         m=edges.size();
         G[from].push_back(m-);
         G[to].push_back(m-);
     }

     bool BFS()
     {
         queue<int> Q;
         memset(vis,,sizeof(vis));
         vis[s]=true;
         d[s]=;
         Q.push(s);
         while(!Q.empty())
         {
             int x=Q.front(); Q.pop();
             for(int i=;i<G[x].size();++i)
             {
                 Edge& e=edges[G[x][i]];
                 if(!vis[e.to] && e.cap>e.flow)
                 {
                     vis[e.to]=true;
                     d[e.to]=d[x]+;
                     Q.push(e.to);
                 }
             }
         }
         return vis[t];
     }

     int DFS(int x,int a)
     {
         if(x==t || a==) return a;
         int flow=, f;
         for(int &i=cur[x];i<G[x].size();++i)
         {
             Edge &e=edges[G[x][i]];
             if(d[e.to]==d[x]+ && (f=DFS(e.to,min(a,e.cap-e.flow) ) )>)
             {
                 e.flow +=f;
                 edges[G[x][i]^].flow -=f;
                 flow +=f;
                 a -=f;
                 if(a==) break;
             }
         }
         return flow;
     }

     int Maxflow(int s,int t)
     {
         this->s=s; this->t=t;
         int flow=;
         while(BFS())
         {
             memset(cur,,sizeof(cur));
             flow +=DFS(s,INF);
         }
         return flow;
     }
 }DC;

 void dfs_s(int u)
 {
     vis[u]=;
     for(int i=;i<DC.G[u].size();i++)
     {
         Edge& e=DC.edges[DC.G[u][i]];
         if(!vis[e.to] && e.cap> && e.cap>e.flow)
             dfs_s(e.to);
     }
 }

 void dfs_t(int u)
 {
     vis[u]=;
     for(int i=;i<DC.G[u].size();i++)
     {
         Edge& e=DC.edges[DC.G[u][i]];
         int tmp=DC.G[u][i];
         if(!vis[e.to] && e.cap== && DC.edges[tmp^].cap>DC.edges[tmp^].flow)  //用正向弧判断
             dfs_t(e.to);
     }
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%d%d%d%d",&n,&m,&a,&b) && (n+m+a+b))
     {
         int src=a, dst=b;
         DC.init(n+);

         for(int i=;i<=m;i++)
         {
             int u, v, w;
             scanf("%d%d%d",&u,&v,&w);
             DC.AddEdge(u,v,w);
             DC.AddEdge(v,u,w);
         }

         DC.Maxflow(src,dst);

         memset(vis,,sizeof(vis));

         dfs_s(src);
         dfs_t(dst);

         bool flag=true;
         for(int i=;i<=n;i++)
         if(!vis[i])  {flag=false;break;}

         if(flag)  printf("UNIQUE\n");
         else printf("AMBIGUOUS\n");
     }
     return ;
 }