Codeforces Round #373 (Div. 2) E. Sasha and Array 线段树维护矩阵

E. Sasha and Array

题目连接：

http://codeforces.com/contest/719/problem/E

Description

Sasha has an array of integers a1, a2, ..., an. You have to perform m queries. There might be queries of two types:

1 l r x — increase all integers on the segment from l to r by values x;
2 l r — find , where f(x) is the x-th Fibonacci number. As this number may be large, you only have to find it modulo 109 + 7.

In this problem we define Fibonacci numbers as follows: f(1) = 1, f(2) = 1, f(x) = f(x - 1) + f(x - 2) for all x > 2.

Sasha is a very talented boy and he managed to perform all queries in five seconds. Will you be able to write the program that performs as well as Sasha?

Input

The first line of the input contains two integers n and m (1 ≤ n ≤ 100 000, 1 ≤ m ≤ 100 000) — the number of elements in the array and the number of queries respectively.

The next line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109).

Then follow m lines with queries descriptions. Each of them contains integers tpi, li, ri and may be xi (1 ≤ tpi ≤ 2, 1 ≤ li ≤ ri ≤ n, 1 ≤ xi ≤ 109). Here tpi = 1 corresponds to the queries of the first type and tpi corresponds to the queries of the second type.

It's guaranteed that the input will contains at least one query of the second type.

Output

For each query of the second type print the answer modulo 109 + 7.

Sample Input

5 4

1 1 2 1 1

2 1 5

1 2 4 2

2 2 4

2 1 5

Sample Output

5

7

9

Hint

题意

给你n个数，两个操作，1是区间增加x，2是查询区间fib(a[i])的和

题解：

回忆一下你怎么做矩阵快速幂fib的，就知道这个更新，其实就是多乘上了一个A^x矩阵。

A = 【0,1;0,0;】这个玩意儿。

然后就可以区间更新呢。

CF官方题解下面有个评论说的很清楚，大家可以看一下。

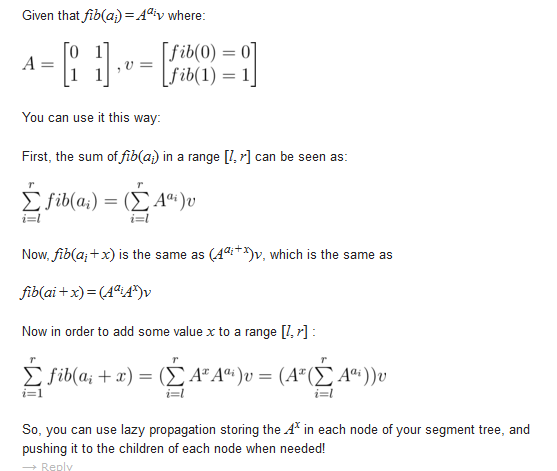
代码

#include<bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
const int maxn = 1e5+5;
struct node
{
    long long a[2][2];
    void reset()
    {
        memset(a,0,sizeof(a));
    }
    void one()
    {
        reset();
        a[0][0]=a[1][1]=1;
    }
};
node add(node A,node B)
{
    node k;k.reset();
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            k.a[i][j]=(A.a[i][j]+B.a[i][j])%mod;
    return k;
}
node mul(node A,node B)
{
    node k;memset(k.a,0,sizeof(k.a));
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
            for(int t=0;t<2;t++)
                k.a[i][j]=(k.a[i][j]+A.a[i][t]*B.a[t][j])%mod;
    return k;
}
node qpow(int p)
{
    node A;
    A.a[0][0]=0,A.a[1][0]=1,A.a[0][1]=1,A.a[1][1]=1;
    node K;
    K.one();
    while(p)
    {
        if(p%2)K=mul(K,A);
        A=mul(A,A);p/=2;
    }
    return K;
}
typedef node SgTreeDataType;
struct treenode
{
  int L , R  , flag;
  SgTreeDataType sum , lazy;
  void update(SgTreeDataType v)
  {
      sum=mul(sum,v);
      lazy=mul(lazy,v);
      flag=1;
  }
};
treenode tree[maxn*4];
int a[maxn];
inline void push_down(int o)
{
    if(tree[o].flag)
    {
        tree[2*o].update(tree[o].lazy) ; tree[2*o+1].update(tree[o].lazy);
        tree[o].flag = 0;tree[o].lazy.one();
    }
}
inline void push_up(int o)
{
    tree[o].sum = add(tree[o*2].sum,tree[o*2+1].sum);
}
node tmp;
inline void build_tree(int L , int R , int o)
{
    tree[o].L = L , tree[o].R = R,tree[o].sum.reset(),tree[o].lazy.one(),tree[o].flag=0;
    if(L==R)
    {
        tree[o].sum=qpow(a[L]);
    }
    if (R > L)
    {
        int mid = (L+R) >> 1;
        build_tree(L,mid,o*2);
        build_tree(mid+1,R,o*2+1);
        push_up(o);
    }
}
inline void update(int QL,int QR,SgTreeDataType v,int o)
{
    int L = tree[o].L , R = tree[o].R;
    if (QL <= L && R <= QR) tree[o].update(v);
    else
    {
        push_down(o);
        int mid = (L+R)>>1;
        if (QL <= mid) update(QL,QR,v,o*2);
        if (QR >  mid) update(QL,QR,v,o*2+1);
        push_up(o);
    }
}
inline SgTreeDataType query(int QL,int QR,int o)
{
    int L = tree[o].L , R = tree[o].R;
    if (QL <= L && R <= QR) return tree[o].sum;
    else
    {
        push_down(o);
        int mid = (L+R)>>1;
        SgTreeDataType res;res.reset();
        if (QL <= mid) res=add(res,query(QL,QR,2*o));
        if (QR > mid) res=add(res,query(QL,QR,2*o+1));
        push_up(o);
        return res;
    }
}
int n,q;
int main()
{
    tmp.a[0][0]=0,tmp.a[1][0]=1,tmp.a[0][1]=1,tmp.a[1][1]=1;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++)scanf("%d",&a[i]);
    build_tree(1,n,1);
    for(int i=1;i<=q;i++)
    {
        int op;scanf("%d",&op);
        if(op==2){
            int a,b;scanf("%d%d",&a,&b);
            printf("%lld\n",query(a,b,1).a[1][0]);
        }
        else{
            int a,b,c;scanf("%d%d%d",&a,&b,&c);
            update(a,b,qpow(c),1);
        }
    }
    return 0;
}