IP地址和子网划分学习笔记之《预备知识：进制计数》

一、序：IP地址和子网划分学习笔记开篇

只要记住你的名字，不管你在世界的哪个地方，我一定会去见你。
——新海诚电影《你的名字》

在我们的日常生活中，每个人的名字对应一个唯一的身（敏）份（感）证（词）号，在Internet上也是一样，每台主机(Host)，包括所有的具有上网功能的电子设备都有IP地址，有了IP地址，这些电子设备联网之后，才能正常通信。

要了解和熟练掌握IP地址和子网的划分，首先必须要对进制数计数有一定的认识，本篇为预备知识：掌握十进制、二进制、十六进制、八进制以及它们之间的关系和互相转换。

IP地址和子网划分学习笔记相关篇章：

1、IP地址和子网划分学习笔记之《预备知识：进制计数》

2、IP地址和子网划分学习笔记之《IP地址详解》

3、IP地址和子网划分学习笔记之《子网掩码详解》

4、IP地址和子网划分学习笔记之《子网划分详解》

5、IP地址和子网划分学习笔记之《超网合并详解》

二、计算机中进制之间的关系和转换

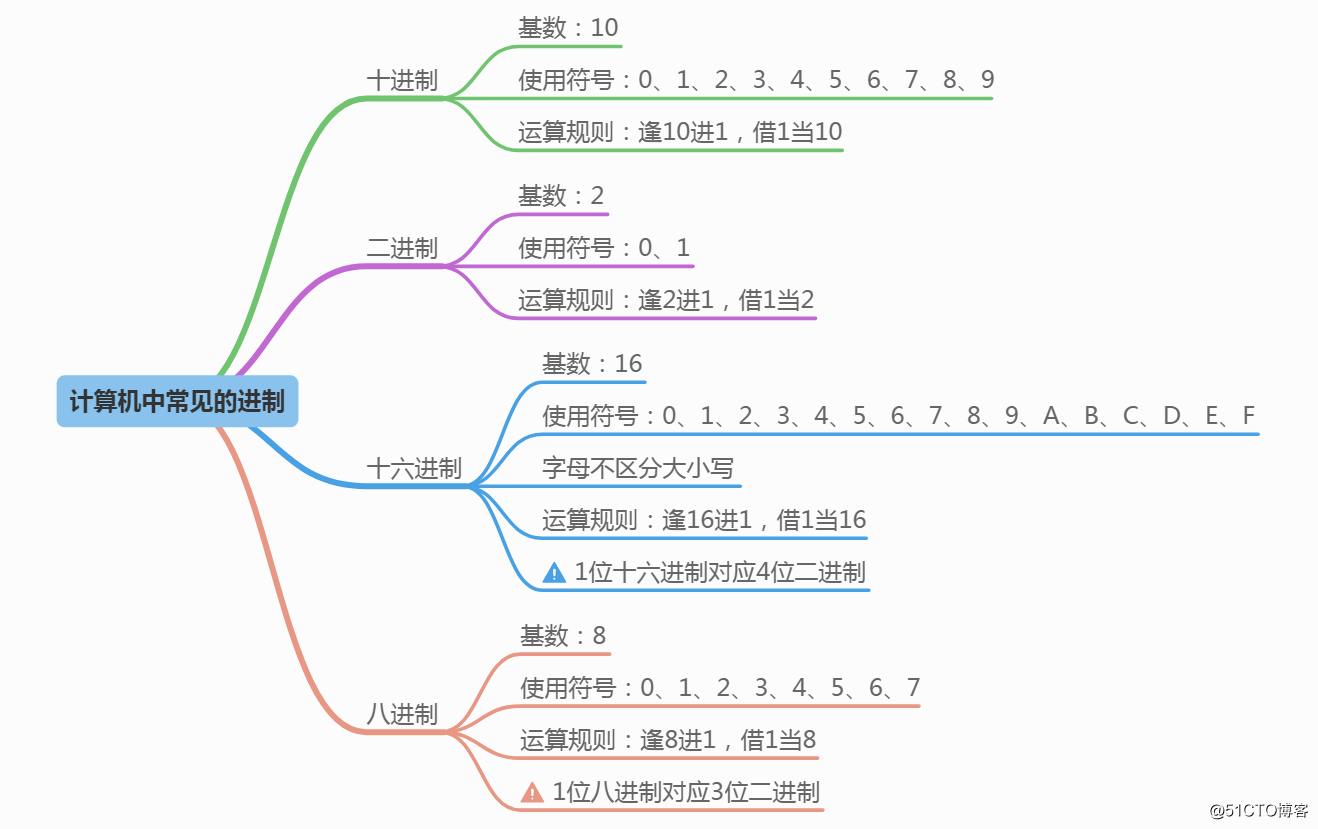
1、计算机中常见的进制

我们的日常生活中常见的十进制，计算机的运行计算基础就是基于二进制来运行，可以简单的理解为：1代表通电（开），0代表断电（关），只是用二进制执行运算，用其他进制表现出来。十六进制常见于内存地址，注册表regedit，MAC地址等。
而计算机中八进制比较少见不常用，一般用于某些编程语言。

计算机本身使用的就是二进制，但是使用起来很不方便的，十六进制或八进制可以很好的解决这个问题（换算的时候1位十六进制数可以用4位二进制数代替，1位八进制数可以用3位二进制数代替）。因为进制越大，数的表达长度也就越短，例如：二进制数111111111111用十六进制表示为FFF，这样更简短，比较节省空间，方便读，也方便记。

2、十进制、二进制、十六进制、八进制之间对照表

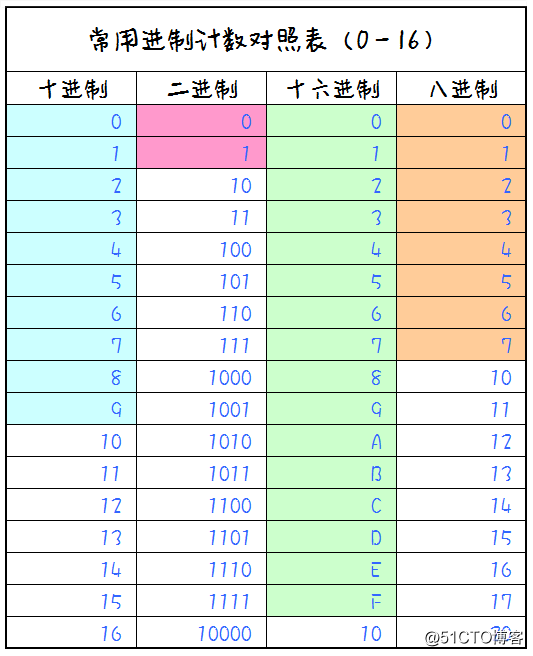
3、二进制、八进制、十六进制数转换成十进制

十进制可以有多位组成，根据十进制的运算规则：逢10进1，借1当10，从右向左依次为个位、十位、百位、千位、万位...
（1024）10 = 1×10^3+0×10^2+2×10^1+4×10^0
= 1000+0+20+4
=（1024）10

由此类似，那么二进制的运算规则：逢2进1，借1当2，也可以由多位数组成，从右向左分别为1位、2位、4位、8位、16位...

为什么称二进制的位数为1位、2位、4位...?
这其实要从十进制的角度看二进制各位数得出的名称，如下表：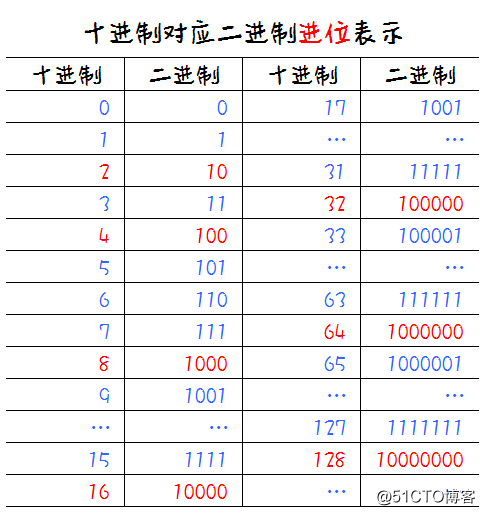

从上表可以看出，当二进制产生进位时，代表的十进制数为2、4、8、16、32、64、128...
二进制虽然只有0和1两个数字，但是由于数字所处的位置不同，表示的数据也不同
例如：
二进制数 “1101”这个二进制数共有4位，由3个1和1个0组成，比如数字1所处位置不同，所代表的大小也不同，其所处位置称作权。从右向左顺序各个位表示十进制的含义：

第一个1表示：1的个数

第二个0表示：2的个数

第三个1表示：4的个数

第四个1表示：8的个数

(在此可以类比十进制1101，由1个1000，1个100，0个10，1个1组成。)
所以，二进制数1101由1个8，1个4，0个2，1个1组成。按各位的权列出：
（1101）2 = 1×2^3+1×2^2+0×2^1+1×2^0
= 8+4+0+1
=（13）10

这种权展开式可以很方便将二进制转换为十进制。
同理，将八进制数1024转换为十进制数
（1024）8 = 1×8^3+0×8^2+2×8^1+4×8^0
= 512+0+16+4
=（532）10

将十六进制数2B5F转换为十进制数
（2B5F）16 = 2×16^3+B×16^2+5×16^1+F×16^0
= 2×16^3+11×16^2+5×16^1+15×16^0
= 8192+2816+80+15
=（11103）10

由此我们可以得到一个非十进制数转换为十进制数的自定义公式：
（X）Z = Xn-1×Z^n-1+ Xn-2×Z^n-2+…+ X1×Z^1+ X0×Z^0
=（Y）10
X表示一个非二进制（多位），Y表示一个十进制数（多位），Z表示各进制的基数，n表示位数。

4、十进制转换成二进制、十六进制、八进制

十进制转换成二进制整数就通常采用“除2取余，逆序排列”的方法。具体做法是用2整除十进制整数，可以得到一个商和余数，再用2去除商，又会得到一个商和余数，如此反复，直到商为0停止。再把先得到的余数作为二进制低位有效位，后得到的余数作为二进制高位有效位，依次排列。
举个示例：将十进制“11”转换为二进制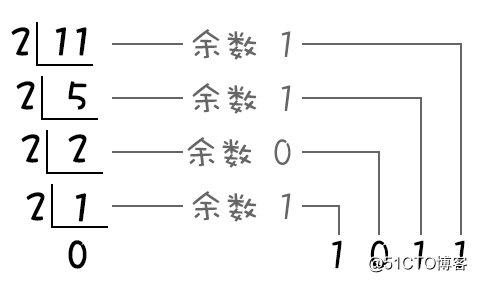

将十进制11转换为二进制数为1011，表示为：（11）10 =（1011）2

同样的，十进制转换为十六进制，采用“除16取余，逆序排列”的方法，十进制转换为八进制采用“除8取余，逆序排列”的方法。

5、进制之间转换小技巧

1位十六进制等于4位二进制
1位八进制等于3位二进制

由于十六进制和八进制的基数问题（太大或不太好算），它们的“幂次方”和“除基数取余”计算起来比较麻烦，为了方便计算，通常建议先把它们转换位二进制后再继续转换为相应的进制。