poj 2947 Widget Factory （高斯消元解同余方程组+判断无解、多解）

http://poj.org/problem?id=2947

血泪史：

CE：poj的string类型要加string库，swap不能直接交换数组

WA：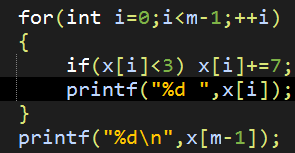

x[m-1]也有可能<3啊Ｏ(≧口≦)Ｏ

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
 
using namespace std;
 
const int mod=;
 
int n,m;
char ch[][] = {"MON", "TUE", "WED", "THU", "FRI", "SAT", "SUN"};  
 
int a[][];
int x[];
 
int inv[];
 
void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c))  c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar();  }
}
 
int getgcd(int a,int b) { return !b ? a : getgcd(b,a%b); }
 
int getlcm(int a,int b) { return a*b/getgcd(a,b); }
 
void preinv()
{
    inv[]=;
    for(int i=;i<=;++i) inv[i]=(-mod/i*inv[mod%i]%mod+mod)%mod;
}
 
int gauss()
{
    int equ=n,var=m;
    int i,j,k;
    int max_r,col;
    int ta,tb,lcm;
    int tmp;
    for(k=,col=;k<equ && col<var;++k,++col)
    {
        max_r=k;
        for(i=k+;i<equ;++i)
            if(abs(a[i][col])>abs(a[max_r][col])) max_r=i;
        if(!a[max_r][col]) { --k; continue; }
        if(k!=max_r)
            for(j=col;j<var+;++j) swap(a[k][j],a[max_r][j]);
        for(i=k+;i<equ;++i)
            if(a[i][col])
            {
                lcm=getlcm(abs(a[i][col]),abs(a[k][col]));
                ta=lcm/abs(a[i][col]);
                tb=lcm/abs(a[k][col]);
                if(a[i][col]*a[k][col]<) tb=-tb;
                for(j=col;j<var+;++j) a[i][j]=((a[i][j]*ta-a[k][j]*tb)%mod+mod)%mod;
            }
    }
    for(int i=k;i<equ;++i)
        if(a[i][var]) return -;
    if(k<var) return -;
    for(int i=var-;i>=;--i)
    {
        tmp=a[i][var];
        for(j=i+;j<var;++j)
            if(a[i][j])
            {
                tmp-=a[i][j]*x[j];
                tmp=(tmp%mod+mod)%mod;
            }
        x[i]=tmp*inv[a[i][i]]%mod;
    }
    return ;
}
 
int turn(char *c)
{
    for(int i=;i<;++i)
        if(!strcmp(c,ch[i])) return i+;
}
 
int main()
{
    int k,xi;
    char c[];
    int s,t;
    preinv();
    while(scanf("%d%d",&m,&n)!=EOF)
    {
        if(!m) return ;
        memset(a,,sizeof(a));
        for(int i=;i<n;++i)
        {
            read(k);
            scanf("%s",c);
            s=turn(c);
            scanf("%s",c);
            t=turn(c);
            a[i][m]=(t-s++)%;
            while(k--)
            {
                read(xi);
                a[i][xi-]++;
            }
        }
        for(int i=;i<n;++i)
            for(int j=;j<m;++j)
                a[i][j]%=mod;
        int ans=gauss();
        if(ans==-) puts("Inconsistent data.");
        else if(ans==-) puts("Multiple solutions.");
        else
        {
            for(int i=;i<m;++i)
            {
                if(x[i]<) x[i]+=;
                printf("%d%c",x[i],i==m- ? '\n' : ' ');
            }
        }
    }
}